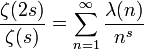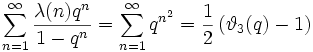Fonction De Liouville

Fonction de Liouville

La fonction de Liouville, notée λ(n) et nommée ainsi en l'honneur du mathématicien français Joseph Liouville, est une fonction importante de la théorie des nombres.

Si n est un entier positif, alors λ(n) est définie par :

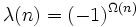$\lambda(n) = (-1)^{\Omega(n)}\,\!$ ,

où Ω(n) est le nombre de diviseurs premiers de n, comptés avec leur ordre de multiplicité. (SIDN A008836).

λ est complètement multiplicative car Ω(n) est additive. Nous avons Ω(1)=0 et par conséquent λ(1)=1. La fonction de Liouville satisfait l'identité :

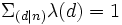$\Sigma_{(d|n)}\lambda(d)=1\,\!$ si n est un carré parfait, et :

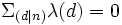$\Sigma_{(d|n)}\lambda(d)=0\,\!$ sinon.

Séries

La série de Dirichlet pour la fonction de Liouville est reliée à la fonction Zeta de Riemann par la formule

$\frac{\zeta(2s)}{\zeta(s)} = \sum_{n=1}^\infty \frac{\lambda(n)}{n^s}$

La série de Lambert pour la fonction de Liouville est

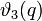$\sum_{n=1}^\infty \frac{\lambda(n)q^n}{1-q^n} = \sum_{n=1}^\infty q^{n^2} = \frac{1}{2}\left(\vartheta_3(q)-1\right)$

où $\vartheta_3(q)$ est une fonction theta de Jacobi.

Conjectures

Pólya a conjecturé que 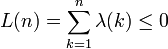$L(n) = \sum_{k=1}^n \lambda(k) \leq 0$ pour n>1. Ceci fut réfuté par Minoru Tanaka, n=906 150 257 étant le plus petit contre-exemple. On ignore si L(n) change de signe infiniment souvent.

Si on définit 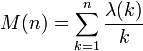$M(n) = \sum_{k=1}^n \frac{\lambda(k)}{k}$ , alors il semblait possible que $M (n) > 0$ pour n suffisamment grand, ce qui a été réfuté en 1958 par Haselgrove. Paul Turán avait montré que cette propriété implique l'hypothèse de Riemann.

Portail des mathématiques

Ce document provient de « Fonction de Liouville ».

Catégorie : Fonction arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction De Liouville de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Fonction de liouville — La fonction de Liouville, notée λ(n) et nommée ainsi en l honneur du mathématicien français Joseph Liouville, est une fonction importante de la théorie des nombres. Si n est un entier positif, alors λ(n) est définie par : , où Ω(n) est le… … Wikipédia en Français
Fonction de Liouville — La fonction de Liouville, notée λ(n) et nommée ainsi en l honneur du mathématicien français Joseph Liouville, est une fonction importante de la théorie des nombres. Si n est un entier positif, alors λ(n) est définie par : , où Ω(n) est le… … Wikipédia en Français
Fonction Multiplicative — En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers entre eux a et b, on… … Wikipédia en Français
Fonction complètement multiplicative — Fonction multiplicative En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers … Wikipédia en Français
Fonction faiblement multiplicative — Fonction multiplicative En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers … Wikipédia en Français
Fonction strictement multiplicative — Fonction multiplicative En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers … Wikipédia en Français
Fonction multiplicative — En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers entre eux a et b, on… … Wikipédia en Français
Fonction Entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction entiere — Fonction entière La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le … Wikipédia en Français
LIOUVILLE (J.) — Joseph Liouville fut un bon artisan des mathématiques, déployant une activité considérable dans l’enseignement et la diffusion des idées mathématiques de son temps; il est le fondateur du Journal de mathématiques pures et appliquées appelé… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Fonction De Liouville