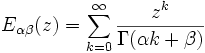Fonction de mittag-leffler
- Fonction de mittag-leffler
-
Fonction de Mittag-Leffler
En mathématiques, la fonction de Mittag-Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag-Leffler, est une fonction spéciale, c’est-à-dire qui ne peut être calculée à partir d'équations rationnelles, qui s'applique dans le plan complexe et dépend de deux paramètres complexes α et β. La fonction est définie pour α > 0 :
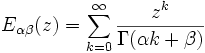
Dans ce cas, la série converge pour toute valeur d'argument z, ce qui fait de la fonction une fonction entière.
Ce résultat est connu sous le nom de théorème de Mittag-Leffler.
La fonction d'erreur
La fonction d'erreur est un cas particulier de la fonction de Mittag-Leffler :
- w(z) = exp( − z2)erfc( − iz) = E1 / 2,1(iz)
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse complexe | Fonction remarquable | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de mittag-leffler de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction De Mittag-Leffler — En mathématiques, la fonction de Mittag Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag Leffler, est une fonction spéciale, c’est à dire qui ne peut être calculée à partir d équations rationnelles, qui s applique dans le plan… … Wikipédia en Français
Fonction de Mittag-Leffler — En mathématiques, la fonction de Mittag Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag Leffler, est une fonction spéciale, c’est à dire qui ne peut être calculée à partir d équations rationnelles, qui s applique dans le plan… … Wikipédia en Français
Théorème de Mittag-Leffler — Fonction de Mittag Leffler En mathématiques, la fonction de Mittag Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag Leffler, est une fonction spéciale, c’est à dire qui ne peut être calculée à partir d équations rationnelles,… … Wikipédia en Français
Mittag-Leffler-Funktion — Die Mittag Leffler Funktion ist eine nach dem Mathematiker Magnus Gösta Mittag Leffler benannte mathematische Funktion, die in den Lösungen von bestimmten gebrochenen Integralgleichungen auftaucht (z. B. bei der Untersuchung von Zufallsbewegungen … Deutsch Wikipedia
Gösta Mittag-Leffler — Pour les articles homonymes, voir Mittag. Gösta Mittag Leffler Gösta Mittag Leffler (16 mars 1846 – 7 juillet … Wikipédia en Français
Fonction Entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction entiere — Fonction entière La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le … Wikipédia en Français
Mittag — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Mittag: Anja Mittag (1985 ), footballeuse allemande Gösta Mittag Leffler (1846 1927), mathématicien suédois Fonction de Mittag Leffler Institut Mittag… … Wikipédia en Français
Fonction entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Histoire De La Fonction Zeta De Riemann — Histoire de la fonction zêta de Riemann Cet article présente une histoire de la fonction zêta de Riemann. Pour une présentation mathématique de la fonction et de ses propriétés, voir : Article principal : fonction zêta de Riemann. Un… … Wikipédia en Français