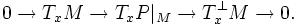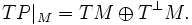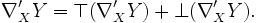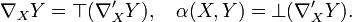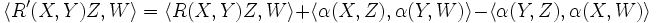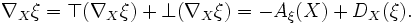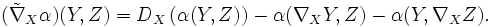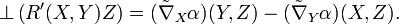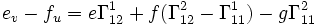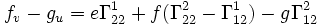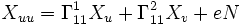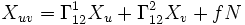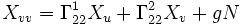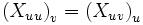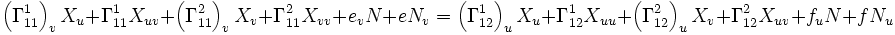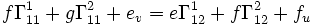Equations de Gauss-Codazzii

Equations de Gauss-Codazzii

Équations de Gauss-Codazzii

En géométrie riemannienne, les équations de Gauss-Codazzi-Mainardi sont des équations fondamentales dans le cadre de la théorie des hypersurfaces plongées dans un espace euclidien, et plus généralement des sous-variétés d'une variété riemannienne. Il existe aussi des applications au cas des hypersurfaces plongées dans une variété pseudo-riemannienne : voir Équations de Gauss-Codazzi (relativité).

Dans la géométrie des surfaces classique, les équations de Gauss-Codazzi-Mainardi sont constituées d'une paire d'équations. La première équation, parfois appelée équation de Gauss relie la courbure intrinsèque (ou courbure de Gauss) de la surface aux dérivées de l'application de Gauss, via la seconde forme fondamentale. Cette équation est la base même du Theorema egregium de Gauss.[1] La seconde équation, parfois appelée équation de Codazzi-Mainardi, est une condition structurelle sur les dérivées secondes de l'application de Gauss.[2] Cette équation comprend la courbure extrinsèque (ou courbure moyenne) de la surface. Ces équations montrent que les composantes de la seconde forme fondamentale et ses dérivées classifie entièrement la surface à une transformation euclidienne près, ce qui revient à un des théorème de Pierre-Ossian Bonnet.[3]

Sommaire

Énoncé formel

Soit i : M ⊂ P une sous-variété n-dimensionelle plongé d'une variété Riemannienne P de dimension n+p. Il existe une inclusion naturelle du fibré tangent de M dans celui de P, et le conoyau est le fibré normal de M :

0\rightarrow T_xM \rightarrow T_xP|_M \rightarrow T_x^\perp M\rightarrow 0.

La métrique donne suite exacte suivante :

TP|_M = TM\oplus T^\perp M.

Suivant cette suite, la connexion de Levi-Civita ∇′ de P se décompose en une composante tangentielle et une composante normale. Pour chaque X ∈ TM et champ de vecteur Y sur M,

\nabla'_X Y = \top(\nabla'_X Y) + \bot(\nabla'_X Y).

Soit

\nabla_X Y = \top(\nabla'_X Y),\quad \alpha(X,Y) = \bot(\nabla'_X Y).

Formule de Gauss[4] donne alors ∇X est la connexion de Levi-Civita pour M, et α est une forme différentielle vectorielle symétrique à valeur dans le fibré normal.

Un corolaire immédiat est l'équation de Gauss. Pour X, Y, Z, W ∈ TM,

\langle R'(X,Y)Z, W\rangle = \langle R(X,Y)Z, W\rangle + \langle \alpha(X,Z), \alpha(Y,W)\rangle -\langle \alpha(Y,Z), \alpha(X,W)\rangle

où R′ est le tenseur de courbure de P et R est celui de M.

L'équation de Weingarten est un analogue de la formule de Gauss pour une connexion dans le fibré normal. Soit X ∈ TM et ξ un champ de vecteurs normaux. On décompose alors la dérivée covariante de ξ sur X en composantes normales et tangentielles :

\nabla_X\xi=\top (\nabla_X\xi) + \bot(\nabla_X\xi) = -A_\xi(X) + D_X(\xi).

Alors

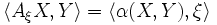
  1. Équations de Weingarten : \langle A_\xi X, Y\rangle = \langle \alpha(X,Y), \xi\rangle
  2. DX est une connexion métrique dans le fibré normal.

Il y a donc un couple de connexions : ∇, définie sur le fibré tangent de M; et D, défini sur le fibré normal de M. Ces deux se combinent pour donner une connexion sur n'importe quel produit tensoriel de TM et T⊥M. En particulier, elles définissent entièrement la dérivée covariante de α :

(\tilde{\nabla}_X \alpha)(Y,Z) = D_X\left(\alpha(Y,Z)\right) - \alpha(\nabla_X Y,Z) - \alpha(Y,\nabla_X Z).

L'équation de Codazzi-Mainardi donne

\bot\left(R'(X,Y)Z\right) = (\tilde{\nabla}_X\alpha)(Y,Z) - (\tilde{\nabla}_Y\alpha)(X,Z).

Énoncé des équations

En géométrie différentielle classique, les équations de Codazzi-Mainardi sont généralement exprimées avec la seconde forme fondamentales :

e_v-f_u=e\Gamma_{12}^1 + f(\Gamma_{12}^2-\Gamma_{11}^1) - g\Gamma_{11}^2
f_v-g_u=e\Gamma_{22}^1 + f(\Gamma_{22}^2-\Gamma_{12}^1) - g\Gamma_{12}^2

Dérivation des équations

Les dérivées secondes d'une surface paramétrique peuvent s'exprimées avec la base {Xu,Xv,N} ainsi que les symboles de Christoffel et la seconde forme fondamentale.

X_{uu}=\Gamma_{11}^1 X_u + \Gamma_{11}^2 X_v + eN
X_{uv}=\Gamma_{12}^1 X_u + \Gamma_{12}^2 X_v + fN
X_{vv}=\Gamma_{22}^1 X_u + \Gamma_{22}^2 X_v + gN

Le théorème de Clairaut énonce que les dérivées partielles suivantes commutent :

\left(X_{uu}\right)_v=\left(X_{uv}\right)_u

Si l'on différencie Xuu par rapport à v et Xuv par rapport à u, on obtient :

\left(\Gamma_{11}^1\right)_v X_u + \Gamma_{11}^1 X_{uv} + \left(\Gamma_{11}^2\right)_v X_v + \Gamma_{11}^2 X_{vv} + e_v N + e N_v = \left(\Gamma_{12}^1\right)_u X_u + \Gamma_{12}^1 X_{uu} + \left(\Gamma_{12}^2\right)_u X_v + \Gamma_{12}^2 X_{uv} + f_u N + f N_u

Si on substitue ensuite les expressions ci-dessus pour les dérivées secondes et qu'on égale les coefficients de N :

f \Gamma_{11}^1 + g \Gamma_{11}^2 + e_v = e \Gamma_{12}^1 + f \Gamma_{12}^2 + f_u

en réarrangeant les termes, on retrouve la première équation de Codazzi-Mainardi.

Sources et références

  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Gauss-Codazzi equations ».
  1. ↑ Gauss (1828).
  2. ↑ Nommée ainsi en l'honneur de Gaspare Mainardi (1856) et Delfino Codazzi (1868-1869), qui ont indépendamment trouvé ce résultat. Cf. Kline (1972), p. 885.
  3. ↑ Bonnet (1867).
  4. ↑ Terminology from Spivak, Volume III.
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « %C3%89quations de Gauss-Codazzii ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equations de Gauss-Codazzii de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Équations de Gauss-Codazzii — En géométrie riemannienne, les équations de Gauss Codazzi Mainardi sont des équations fondamentales dans le cadre de la théorie des hypersurfaces plongées dans un espace euclidien, et plus généralement des sous variétés d une variété riemannienne …   Wikipédia en Français

  • Équations de gauss-codazzii — En géométrie riemannienne, les équations de Gauss Codazzi Mainardi sont des équations fondamentales dans le cadre de la théorie des hypersurfaces plongées dans un espace euclidien, et plus généralement des sous variétés d une variété riemannienne …   Wikipédia en Français

  • Gauss (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carl Friedrich Gauss (1777 1855), mathématicien, astronome et physicien allemand. Le gauss, une unité de mesure du champ magnétique, noté G. GAUSS, un… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Delfino Codazzi — Pour les articles homonymes, voir Codazzi. Delfino Codazzi (né le 7 mars 1824 à Lodi, en Lombardie, alors dans le Royaume lombard vénitien et mort le 21 juillet 1873 à Pavie) est un mathématicien italien du XIXe siècle …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”