Equations de Lagrange

Equations de Lagrange: Équations de Lagrange

Pour les articles homonymes, voir Lagrange.

Les équations de Lagrange, découvertes en 1788 par le mathématicien Joseph Louis Lagrange, sont une reformulation de la mécanique classique. En mécanique lagrangienne, la trajectoire d'un objet est obtenue en cherchant à minimiser une certaine quantité, appelée action (physique). Le principe de moindre action indique qu'un objet suit la trajectoire qui minimise l'action à chaque instant et les équations de Lagrange reformulent dans ce contexte les lois de la mécanique classique découvertes par Isaac Newton.

En mécanique, les équations de Lagrange permettent d'obtenir très facilement les équations du mouvement d'un système complexe sans avoir à utiliser la notion de force.

Pour un système à $N$ degrés de liberté décrit par $N$ coordonnées généralisées $q i$ , on exprime le lagrangien $L$ à partir des coordonnées généralisées $q i$ et de leurs dérivées par rapport au temps 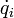$\dot{q}_{i}$ comme la différence entre l'énergie cinétique et l'énergie potentielle. Comme le temps peut figurer explicitement dans le lagrangien, il dépend au final de $2 N + 1$ variables.

Lorsqu'aucun effort extérieur n'est appliqué sur le système, les équations de Lagrange ont la forme suivante :
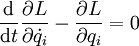
$\frac{\mathrm d}{\mathrm dt} \frac{\partial L}{\partial \dot{q}_{i}} - \frac{\partial L}{\partial q_{i}} = 0$
Ces équations peuvent se déduire directement des lois de la mécanique classique. Il y a une équation pour chaque coordonnée généralisée 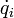$\dot{q}_{i}$ . L'un des intérêts de ces équations est de pouvoir choisir le système de variables le plus adapté pour décrire le système.

En mécanique classique, le paramètre est le temps et ces équations sont les équations de Lagrange proprement dites.

Si le paramètre est la longueur de la trajectoire, ces équations fournissent l'équation géodésique.

Établissement des équations

Étant donné un système de coordonnées quelconque $x i$ , une variable $τ$ permettant de paramétrer les trajectoires, on considère une fonction $L$ qui ne dépend que des variables $x i$ et leur dérivée totale par rapport à $τ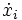$ , $\dot{x}_i$ . On veut trouver les trajectoires $x i (τ)$ d'extrémités données $τ 1$ et $τ 2$ , qui minimisent l'intégrale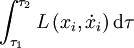
$\int_{\tau_1}^{\tau_2} L\left(x_i, \dot{x}_i\right) \mathrm d\tau$
Considérons une trajectoire infiniment voisine $x'(τ) = x (τ) + εξ(τ)$ avec $ε$ un infiniment petit et $ξ(τ 1) = ξ(τ 2) = 0$ . Supposant que les solutions sont trouvées et $ξ(τ 1)$ donné, la fonction
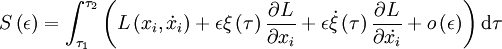
$S\left(\epsilon\right) = \int_{\tau_1}^{\tau_2} \left(L\left(x_i, \dot{x}_i\right) + \epsilon \xi\left(\tau\right) \frac{\partial L}{\partial x_i} + \epsilon \dot{\xi}\left(\tau\right) \frac{\partial L}{\partial \dot{x_i}} + o\left(\epsilon\right) \right)\mathrm d\tau$
est minimale pour $ε = 0$ :
$0 = \left[ \frac{\mathrm dS}{\mathrm d\epsilon} \right] \left(0\right) = \int_{\tau_1}^{\tau_2} \left( \xi\left(\tau\right) \frac{\partial L}{\partial x_i} + \dot{\xi}\left(\tau\right) \frac{\partial L}{\partial \dot{x_i}} \right)\mathrm d\tau$
Intégrant par parties le second terme sous l'intégrale et profitant du fait que $ξ$ a été supposée nulle aux bornes, on a
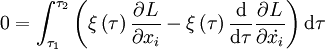$0 = \int_{\tau_1}^{\tau_2} \left(\xi\left(\tau\right) \frac{\partial L}{\partial x_i} - \xi\left(\tau\right) \frac{\mathrm d}{\mathrm d\tau} \frac{\partial L}{\partial \dot{x_i}} \right)\mathrm d\tau$ .
Comme la fonction $ξ$ est quelconque, on doit avoir
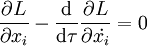
$\frac{\partial L}{\partial x_i} - \frac{\mathrm d}{\mathrm d\tau} \frac{\partial L}{\partial \dot{x_i}} = 0$
Efforts extérieurs

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Lorsqu'une force conservative $F c$ dérivant d'un potentiel $V$ est appliquée au système, l'équation ci-dessus reste valable, on doit juste modifier le lagrangien $L$ :
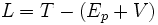
$L = T - (E_p+V)~$
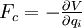
où $T$ est l'énergie cinétique, $E p$ l'énergie potentielle (de gravité ou/et élastique) et $V$ l'énergie potentielle associée au champ de force $V = x T F c$ , tel que $F_c=-\tfrac{\partial V}{\partial q_{i}}$

Lorsqu'une force non conservative $F$ est appliquée sur le système au point $P = (x, y, z)$ , les équations de Lagrange deviennent alors :
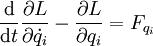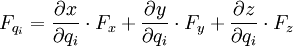
$\frac{\mathrm d}{\mathrm dt} \frac{\partial L}{\partial \dot{q}_{i}} - \frac{\partial L}{\partial q_{i}} = F_{q_i}$ où $F_{q_i}=\frac{\partial x}{\partial q_{i}}\cdot F_{x}+\frac{\partial y}{\partial q_{i}}\cdot F_{y}+\frac{\partial z}{\partial q_{i}}\cdot F_{z}$
Exemples

Pendule double ;

Pendule sphérique ;

Équation géodésique.

Portail des mathématiques

Ce document provient de « %C3%89quations de Lagrange ».

Catégories : Équation différentielle | Joseph-Louis Lagrange

Contenu soumis à la licence CC-BY-SA. Source : Article Equations de Lagrange de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Équations de lagrange — Pour les articles homonymes, voir Lagrange. Les équations de Lagrange, découvertes en 1788 par le mathématicien Joseph Louis Lagrange, sont une reformulation de la mécanique classique. En mécanique lagrangienne, la trajectoire d un objet est… … Wikipédia en Français
Équations de Lagrange — Pour les articles homonymes, voir Lagrange. Les équations de Lagrange, découvertes en 1788 par le mathématicien Joseph Louis Lagrange, sont une reformulation de la mécanique classique. Sommaire 1 Equations de première espèce … Wikipédia en Français
Lagrange — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronymes 1.1 Lagrange 1.2 … Wikipédia en Français
LAGRANGE (J. L.) — Au crépuscule du XVIIIe siècle, le mathématicien Lagrange a donné au calcul des variations sa formulation générale en l’abordant de manière purement analytique; il appliquera ses méthodes à la mécanique dont il donne un exposé systématique qui… … Encyclopédie Universelle
ÉQUATIONS ALGÉBRIQUES — Dès la plus haute antiquité, on rencontre, à l’occasion de problèmes concrets, des exemples de résolution d’équations du premier et du second degré, et, jusqu’au début du XIXe siècle, l’étude des équations constitue l’unique préoccupation des… … Encyclopédie Universelle
Lagrange — (spr. grángsch), Jos. Louis, Mathematiker, geb. 25. Jan. 1736 zu Turin, 1766 87 Direktor der mathem. Klasse der Berliner Akademie, später Prof. an der Polytechnischen Schule in Paris, gest. 10. April 1813; Hauptwerke: »Théorie des fonctions… … Kleines Konversations-Lexikon
Lagrange — (Lagrangsch), Jos. Louis, ausgezeichneter Mathematiker, geb. 1736 zu Turin aus einer französ. Familie. löste schon in seinem 19. Jahre die von Euler gestellte isoperimetrische Aufgabe, ward dann Professor der Mathematik in Turin, erhielt später… … Herders Conversations-Lexikon
Lagrange multiplier — Figure 1: Find x and y to maximize f(x,y) subject to a constraint (shown in red) g(x,y) = c … Wikipedia
Équations diophantiennes — Équation diophantienne Édition de 1670 des Arithmétiques de Diophante d Alexandrie. Une équation diophantienne, en mathématiques, est une équation dont les coefficients sont des nombres entiers et dont les solutions recherchées sont également… … Wikipédia en Français
Lagrange multipliers — In mathematical optimization problems, the method of Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the extrema of a function of several variables subject to one or more constraints; it is the basic tool in… … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Equations de Lagrange

Équations de Lagrange

Établissement des équations

Efforts extérieurs

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Equations de Lagrange

Équations de Lagrange

Établissement des équations

Efforts extérieurs

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link