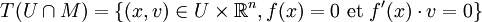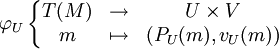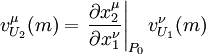- Fibre tangent
-
Fibré tangent
En géométrie différentielle le fibré tangent TM associé à une variété différentielle M est la somme disjointe de tous les espaces tangents en tous les points de la variété. Le fibré tangent est lui-même une variété différentielle, et un espace fibré de base M
Cas des sous-variétés
Supposons que M soit une sous-variété de classe Ck (k ≥ 1) et de dimension d de
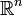 . On peut voir alors TM comme l'ensemble des couples
. On peut voir alors TM comme l'ensemble des couples 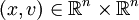 formés d'un point
formés d'un point 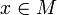 et d'un vecteur v tangent à M en x. (passer à
et d'un vecteur v tangent à M en x. (passer à 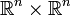 permet de voir les espaces tangents aux différents points comme des ensembles disjoints.)
permet de voir les espaces tangents aux différents points comme des ensembles disjoints.)On obtient ainsi une sous-variété de classe Ck − 1 et de dimension 2d de
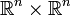 En effet, pour tout point de M, il existe un ouvert
En effet, pour tout point de M, il existe un ouvert 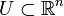 et une submersion
et une submersion 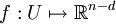 (de classe Ck) tels que
(de classe Ck) tels que 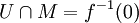 . On en déduit que
. On en déduit queMais l'application
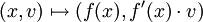 est une submersion de classe Ck − 1 de
est une submersion de classe Ck − 1 de 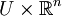 dans
dans 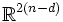
Exemple. Le fibré tangent au cercle
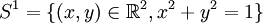 apparaît ainsi comme la sous-variété
apparaît ainsi comme la sous-variété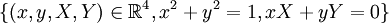 .
.
Il est difféomorphe au cylindre
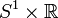 (voir ci-contre).
(voir ci-contre).Définition formelle
On définit T(M) en se donnant pour chaque ouvert U de M une trivialisation locale
où V est un espace vectoriel isomorphe à l'espace tangent à M en n'importe quel
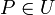 et pour chaque
et pour chaque 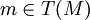 , vU(m) appartient à l'espace tangent à M en PU(m) .
, vU(m) appartient à l'espace tangent à M en PU(m) .Par ailleurs
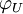 doit satisfaire à la condition de recollement suivante : Si
doit satisfaire à la condition de recollement suivante : Si 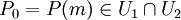 où
où 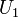 et
et 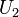 sont des ouverts associés à des cartes
sont des ouverts associés à des cartes 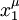 et
et 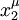 alors on doit avoir (en notation de coordonnées pour les vecteurs
alors on doit avoir (en notation de coordonnées pour les vecteurs 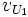 et
et 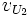 )
)où on a adopté la convention de sommation d'indices répétés d'Einstein.
- Portail des mathématiques
Catégorie : Géométrie différentielle
Wikimedia Foundation. 2010.