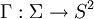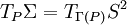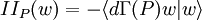Endomorphisme de Weingarten
- Endomorphisme de Weingarten
-
Application de Gauss
En géométrie différentielle classique, l'application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d'accéder à la seconde forme fondamentale. Elle tient son nom du mathématicien allemand Carl Friedrich Gauss.
Application de Gauss
Soit Σ une surface orientée de classe Ck + 1 de R3.
Pour P un point de Σ, il existe un unique vecteur normal unitaire Γ(P) compatible avec l'orientation de Σ. L'application de Gauss est l'application de classe Ck :
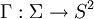
On dispose d'une identification naturelle :
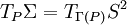
Endomorphisme de Weingarten
La différentielle de l'application de Gauss, vue comme opérateur linéaire de TPΣ, est un opérateur symétrique (appelé endomorphisme de Weingarten) dont la forme quadratique associée est la seconde forme fondamentale IIP de Σ en P.
De manière plus précise, pour tout vecteur tangent 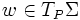 , on a :
, on a :
 Portail de la géométrie
Portail de la géométrie
Catégories : Géométrie différentielle classique | Carl Friedrich Gauss
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Endomorphisme de Weingarten de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Lexique Des Surfaces — Application de Gauss : application différentiable sur les surfaces Axe de symétrie : droite d une symétrie axiale laissant globalement invariante la surface. Calcul différentiel : étude des variations au premier ordre d une… … Wikipédia en Français
Lexique des surfaces — Application de Gauss : application différentiable sur les surfaces Axe de symétrie : droite d une symétrie axiale laissant globalement invariante la surface. Calcul différentiel : étude des variations au premier ordre d une… … Wikipédia en Français
Courbure — Intuitivement, courbe s oppose à droit : la courbure d un objet géométrique est une mesure quantitative du caractère « plus ou moins courbé » de cet objet. Par exemple : dans le plan euclidien, une ligne droite est un objet à… … Wikipédia en Français
Rayon De Courbure — Courbure Intuitivement, courbe s oppose à droit : la courbure d un objet géométrique est une mesure quantitative du caractère « plus ou moins courbé » de cet objet. Par exemple : dans le plan euclidien, une ligne droite est un … Wikipédia en Français
Application de Gauss — L application de Gauss définit une correspondance entre chaque point de l une courbe ou d une surface et un point du cercle ou de la sphère unité En géométrie différentielle classique, l application de Gauss est une application naturelle… … Wikipédia en Français
Application De Gauss — En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde forme fondamentale. Elle… … Wikipédia en Français
Application de gauss — En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde forme fondamentale. Elle… … Wikipédia en Français
Courbure De Gauss — La courbure de Gauss d une surface paramétrée X en X(P) est le produit des courbures principales. De manière équivalente, la courbure de Gauss est le déterminant de l endomorphisme de Weingarten. Le tableau suivant liste les courbures de Gauss de … Wikipédia en Français
Courbure Principale — Les courbures principales d une surface sont les courbures de cette surface selon 2 directions perpendiculaires appelées directions principales. On montre que ce sont les courbures minimales et maximales rencontrées en faisant tourner le plan de… … Wikipédia en Français
Courbure de Gauss — La courbure de Gauss d une surface paramétrée X en X(P) est le produit des courbures principales. De manière équivalente, la courbure de Gauss est le déterminant de l endomorphisme de Weingarten. Le tableau suivant liste les courbures de Gauss de … Wikipédia en Français
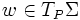 , on a :
, on a :