Application de Gauss

Application de Gauss
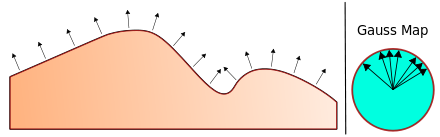
L'application de Gauss définit une correspondance entre chaque point de l'une courbe ou d'une surface et un point du cercle ou de la sphère unité

En géométrie différentielle classique, l'application de Gauss est une application naturelle différentiable sur une surface de \R^3, à valeurs dans la sphère unité S2, et dont la différentielle permet d'accéder à la seconde forme fondamentale. Elle tient son nom du mathématicien allemand Carl Friedrich Gauss.

Application de Gauss

Soit Σ une surface orientée de classe Ck + 1 de \R^3.

Pour P un point de Σ, il existe un unique vecteur normal unitaire Γ(P) compatible avec l'orientation de Σ. L'application de Gauss est l'application de classe Ck :

\Gamma : \Sigma\rightarrow S^2.

On dispose d'une identification naturelle :

T_P\Sigma=T_{\Gamma(P)}S^2~.

Endomorphisme de Weingarten

La différentielle de l'application de Gauss, vue comme opérateur linéaire de TPΣ, est un opérateur symétrique (appelé endomorphisme de Weingarten (de)) dont la forme quadratique associée est la seconde forme fondamentale \mathrm I\!\mathrm I_P de Σ en P.

De manière plus précise, pour tout vecteur tangent w\in T_P\Sigma, on a :

\mathrm I\!\mathrm I_P(w)=-\langle d\Gamma(P)w|w \rangle.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Application de Gauss de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Application De Gauss — En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde forme fondamentale. Elle… …   Wikipédia en Français

  • Application de gauss — En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde forme fondamentale. Elle… …   Wikipédia en Français

  • Gauss (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carl Friedrich Gauss (1777 1855), mathématicien, astronome et physicien allemand. Le gauss, une unité de mesure du champ magnétique, noté G. GAUSS, un… …   Wikipédia en Français

  • GAUSS (C. F.) — L’œuvre du mathématicien allemand Carl Friedrich Gauss (né à Brunswick, mort à Göttingen) est un monument d’une ampleur et d’une richesse sans égale: non seulement il y a Gauss mathématicien, mais il y a aussi le calculateur, le géodésien,… …   Encyclopédie Universelle

  • Application Linéaire — En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire définie dans ces espaces …   Wikipédia en Français

  • Application lineaire — Application linéaire En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire… …   Wikipédia en Français

  • Application trilinéaire — Application linéaire En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire… …   Wikipédia en Français

  • Application Multilinéaire — En algèbre linéaire, une application multilinéaire est une application à plusieurs variables vectorielles qui est linéaire en chaque variable. Quelques exemples classiques : Le produit scalaire est une fonction bilinéaire symétrique à deux… …   Wikipédia en Français

  • Application multilineaire — Application multilinéaire En algèbre linéaire, une application multilinéaire est une application à plusieurs variables vectorielles qui est linéaire en chaque variable. Quelques exemples classiques : Le produit scalaire est une fonction… …   Wikipédia en Français

  • Application linéaire canoniquement associée à une matrice — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”