Traite projectif des coniques

Les coniques ont été définies de mille manières au cours des siècles, chacune ayant ses avantages et ses inconvénients. Actuellement on aime les définir par la notion monofocale d'excentricité (voir conique). Avantages : il n'y a que des calculs, ils sont du niveau terminale de lycée ; inconvénients : un peu trop de géométrie analytique, peu de dessin. Une autre approche est classique, elle définit une conique comme l'intersection d'un plan et d'un cône de révolution; on pourrait lui reprocher de nécessiter la connaissance du cercle, donc la connaissance préalable de la notion de distance ou de la notion d'angle droit, donc d'une connaissance préliminaire d'un espace métrique. Or le dessin des coniques dans un plan, fût-il euclidien sans le savoir, devrait se dispenser de tels prérequis. Une approche purement géométrique à base de règle et crayon, sans équerre ni compas ni double décimètre est présentée ici. On démarre avec quelques axiomes de plans projectifs, ce qui est une expression bien savante pour désigner les alignements et les intersections, on continue le plus loin possible sans utiliser les distances ni les angles. Dans un espace géométrique axiomatisé, fruit de la seule imagination des mathématiciens, on crée des êtres mathématiques particuliers, les coniques, et on se demande si elles peuvent coïncider avec nos coniques traditionnelles.

Sommaire 1 Les axiomes préalables 2 Anticipation : hexagone de Brianchon et hexagramme de Pascal 3 La définition d’un ensemble pascalien 3.1 Vocabulaire nécessaire 3.2 Ensemble pascalien, définition 3.3 Besoin d’un concept-clef 4 Ce que l'on sait de l'approche de Pascal lui-même 5 Plan projectif pappusien et coniques. 6 Plan projectif fondamental et coniques. 7 Plan projectif homogène et coniques. 8 Pour approfondir

Les axiomes préalables

• Un plan projectif (PPI) d’incidence est un PP qui vérifie les axiomes :

• Il existe au moins 2 points.
• Chaque droite possède au moins 3 points.
• Pour deux points distincts il existe une et une seule droite qui leur est incidente.
• Deux droites distinctes ont un et un seul point commun.
• Pour toute droite il existe au moins un point non incident à cette droite.
• (Auxquels on ajoute l’axiome « invisible » d’abondance : toute droite et tout point du PPI possèdent respectivement autant de points et de droites qu’il est nécessaire pour que la configuration étudiée ne soit pas nécessairement dégénérée).

• Un plan projectif arguésien (PPA) est un PPI qui vérifie l’axiome de Desargues : Soient ABC et A'B'C' deux triangles sans point commun tels que les droites (AA'), (BB'), (CC') sont incidentes à un même point alors les points d'intersection des droites (AB) et (A'B'), (AC) et (A'C'), (BC) et (B'C') sont incidents à une même droite.
• Un plan projectif de Pappus (PPP) est un PPI qui vérifie l’axiome de Pappus : Dans un plan , soient A1, B1, C1 trois points distincts quelconques alignés sur une droite quelconque (d), et soient A2, B2, C2 trois autres points distincts quelconques alignés sur une autre droite quelconque (d'), alors les points A intersection de (B2C1) avec (C2B1), B intersection de (A2C1) avec (C2A1), C intersection de (B2A1) avec (A2B1) sont alignés.

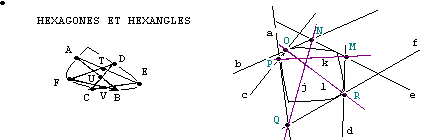
Anticipation : hexagone de Brianchon et hexagramme de Pascal

Les trois questions importantes que posent les coniques sont :

• intersection avec une droite
• tangente en un point
• nombre de points nécessaires et suffisants pour définir une conique ?

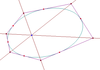
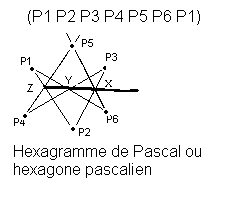
Annonçons tout de suite avant de les démontrer deux grands théorèmes des coniques. Soit un hexagone inscrit dans une conique. Soient A, B et C les points d'intersection des côtés opposés de l'hexagone s'ils existent. Le théorème de Pascal affirme que A, B et C sont alignés. La droite que forme cet alignement est appelée droite de Pascal. La figure obtenue par la construction est appelée hexagramme mystique. Ce théorème est le dual du théorème de Brianchon qui s'énonce ainsi : les diagonales joignant les sommets opposés d'un hexagone sont concourantes si et seulement si cet hexagone est circonscrit à une conique.

Questions soulevées par l'explosion combinatoire.

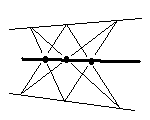
La configuration de Pappus offre une forte permutation : il y a 6 hexagrammes non dégénérés (A1 C2 B1 A2 C1 B2 ; A1 C2 B1 B2 C1 A2 ; A1 B2 B1 C2 C1 A2 ; A1 B2 B1 A2 C1 C2 ; A1 A2 B1 B2 C1 C2 ; A1 A2 B1 C2 C1 B2 ), donc 6 droites de Pappus. Quelles sont les propriétés de ces 6 droites ? En fait on peut démontrer qu'elles sont concourantes en deux groupes de 3. Mais de quels axiomes minimaux a-t-on besoin pour démontrer cette propriété ? L'axiome fondamental de la géométrie projective est-il indispensable ? L'axiome de Desargues suffirait-il ? Quant à l'hexagramme de Pascal, de nombreux mathématiciens du XIX^e siècle se sont penchés sur les diverses permutations du parcours des 6 points. Il s'agit particulièrement de Bauer, Catalan, Cayley, Fontaneau, Gräfe, Grossmann, Hesse, Jörres, Kirkman, Ladd-Franklin-Christine, Little , Lüroth, Meyer, Molk, Plücker, George Salmon, Jakob Steiner, Veronese-G., von Staudt. Avec 6 points, on peut réaliser 60 parcours hexagonaux, donc 60 droites de Pascal. Quelles sont les propriétés de ces 60 droites, comment sont disposées leurs intersections dans le plan ? Quel rapport avec les 60 points de Brianchon que l'on peut dualement envisager ? Par exemple Steiner a montré qu'elles sont concourantes 3 à 3, d'où 20 «points de Steiner». Comment sont disposés ces points, à quel sous-ensemble de permutation correspond chaque point ? Quelles sont leur 20 polaires, ont-elles un rapport avec les 60 droites de Pascal? Ce regroupement par 3 peut-il, comme celui de la figure de Pappus, être démontré par l'axiome de Desargues ou doit-on faire appel à l'axiome fondamental de la géométrie projective ? Ces propriétés ont-elles un lien avec la conservation du rapport anharmonique sur une conique ? Comment, à partir de la découverte de la perspective à la Renaissance en est-on arrivé à se poser ce type de problématique?

La définition d’un ensemble pascalien

Vocabulaire nécessaire

• Dans la pratique. Hormis dans quelques rares cas cruciaux, les auteurs tolèrent les approximations de langage.

Si l’ordre est indifférent, on parlera d’un ensemble de 6 points {A ;B ;C ;D ;E ;F}, d’un ensemble de 6 droites {a ;b ;c ;d ;e ;f } ou {(AB) ;(BF) ;(DC) ;(AE) ;(CE) ;(FD)}.

Si l’ordre est important, on écrira des n-uplets rebouclés, par exemple (A-B-F-D-C-E-A) ou (e-b-c-a-f-d-e) = [(MN)-(NO)-(OP)-(PQ)-(QR)-(RM)-(MN)] = par tolérance(M-N-O-P-Q-R-M), le contexte seul permettant de lever l’ambiguïté ; dans un contexte de Pascal on sait qu’on travaille sur des points, qu’on examine l’alignement de TUV ; dans un contexte de Brianchon, on travaille sur des droites, on examine la convergence de j,k,l.

Ensemble pascalien, définition

• Hexagone pascalien ou hexagramme de Pascal. Définition : un hexagone pascalien

1. est un hexagone ordonné
2. dont les croisillons opposés forment trois points alignés.

Ce dernier point est équivalent à l'existence d'une conique circonscrite à l'hexagone. Cette conique pouvant être dégénérée en droites, on remarque que la configuration de Pappus est un cas particulier d'hexagramme de Pascal.

Besoin d’un concept-clef

On peut choisir un concept typiquement projectif, c'est à dire composé uniquement d'alignements et d'intersections.

Définition d'une conique. Dans un plan projectif d'incidence, une conique est un ensemble C maximal de points tel que tous les hexagrammes ordonnés construits avec 6 points distincts quelconques de cet ensemble soient pascaliens.

Par ensemble maximal possédant la propriété on entend: Si l'on ajoute n'importe quel nouveau point à cet ensemble, alors au moins un hexagramme ordonné contenant ce nouveau point n'a pas la propriété souhaitée.

Ce que l'on sait de l'approche de Pascal lui-même

• Pascal, Œuvres complètes, Bibliothèque de la Pléiade, Paris, Gallimard, nouvelle édition de 1998 par Michel le Guern.

Blaise Pascal (1623-1662) durant sa courte vie a écrit quatre traités de géométrie dont un est perdu, malheureusement c'est celui qui approfondissait les coniques.

Plan projectif pappusien et coniques.

Voir Traité projectif des coniques/Dans un plan pappusien.

• Substitution de deux voisins.

• Existe-t-il une tangente dans un plan projectif pappusien? (Oui)

• Intersection droite/conique dans un plan projectif pappusien.

• Polaire dans un plan projectif pappusien.
• Hexagrammes mystiques et géométrie euclidienne.

Voir Traité projectif des coniques/Dans un plan pappusien--->

Plan projectif fondamental et coniques.

Plan projectif homogène et coniques.

Pour approfondir

• Rappels: Axiomes de plans projectifs puis Axiomes de plans projectifs/homogènes puis Axiomes de plans projectifs/Suite des axiomes
• Traité projectif des coniques/Dans un plan pappusien
• La vie de Blaise Pascal
• Un site où sont donnés de nombreux développements sur le Théorème de Pappus : Merveilleux Pappus

Articles de Géométrie projective ou voisins à consulter.

[modifier]

Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes  • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques)

• Portail de la géométrie