- Diviser
-
Division
 Pour les articles homonymes, voir division (homonymie).
Pour les articles homonymes, voir division (homonymie).La division est une loi de composition qui à deux nombres associe le produit du premier par l'inverse du second. Si un nombre est non nul, la fonction "division par ce nombre" est la réciproque de la fonction "multiplication par ce nombre".
On distingue couramment la division "exacte" (celle dont on parle ici) de la division "avec reste" (la division euclidienne). Le résultat d'une division s'appelle le quotient.
Sommaire
Problématique
La division sert :
- à faire un partage équitable entre un nombre de parts déterminé à l'avance, et donc à déterminer la taille d'une part. Par exemple :
- Question : Si on répartit équitablement 500 grammes de poudre de perlimpimpin entre huit personnes, combien chacune d'elle obtiendra-t-elle ?
- Réponse :
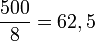 , chacun obtient 62,5 grammes de poudre de perlimpimpin
, chacun obtient 62,5 grammes de poudre de perlimpimpin
- à déterminer le nombre de parts possible, d'une taille déterminée à l'avance. Par exemple :
- Question : Si on répartit 500 grammes de poudre de perlimpimpin par tranche de 70 g, combien de personnes pourra-t-on servir ?
- Réponse :
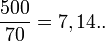 , on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (...)
, on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (...)
Vocabulaire et notations - historique
Le symbole actuel de la division est un trait horizontal séparant le numérateur (dividende) du dénominateur (diviseur). Par exemple, a divisé par b se note
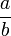 .
.Le dénominateur donne la dénomination et le numérateur énumère :
 indique qu'il s'agit de quarts, et qu'il y en a trois → trois quarts
indique qu'il s'agit de quarts, et qu'il y en a trois → trois quartsDiophante et les Romains, au IVe siècle écrivaient déjà des fractions sous une forme semblable, les Indiens également au XIIe siècle et la notation moderne fut adoptée par les Arabes.
Le symbole : a été plus tard utilisé par Leibniz.
Les fabricants de calculatrices impriment les symboles ÷ ou / sur la touche « opérateur division ». L'utilisation de ces symboles est plus ambiguë que la barre de fraction, puisqu'elle demande de définir des priorités, mais elle est pratique pour l'écriture « en ligne » utilisée en imprimerie ou sur un écran.
Aujourd'hui en France, en classe de 6e de collège, les notations ÷, :' et / sont utilisées, car la division a pour les élèves un statut d'opération. Une nuance de sens est communément admise :
- a ÷ b et a : b désignent une opération (non effectuée), et le vocabulaire approprié est dividende pour a et diviseur pour b ;
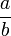 et a / b désignent l'écriture fractionnaire du résultat de cette opération, et le vocabulaire approprié est numérateur pour a et dénominateur pour b.
et a / b désignent l'écriture fractionnaire du résultat de cette opération, et le vocabulaire approprié est numérateur pour a et dénominateur pour b.
Définition
Étant donné un anneau intègre (A, +, ×), la division sur A est la loi de composition :
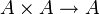 , notée par exemple « ÷ », telle que
, notée par exemple « ÷ », telle que 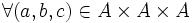 , a ÷ b = c si et seulement si b × c = a.
, a ÷ b = c si et seulement si b × c = a.L'intégrité de l'anneau assure que la division a bien un résultat unique. Par contre, elle n'est définie que sur
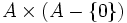 si et seulement si A est un corps, et en aucun cas définie pour b = 0.
si et seulement si A est un corps, et en aucun cas définie pour b = 0.Si la division n'est pas définie partout, on peut étendre conjointement la division et l'ensemble A: Dans le cas commutatif, on définit sur
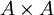 une relation d'équivalence
une relation d'équivalence 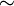 par
par 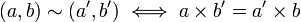 et on écrit a ÷ b la classe de (a,b) dans l'anneau quotient. Cet anneau quotien est un corps dont le neutre est la classe 1 ÷ 1. C'est ainsi que l'on construit
et on écrit a ÷ b la classe de (a,b) dans l'anneau quotient. Cet anneau quotien est un corps dont le neutre est la classe 1 ÷ 1. C'est ainsi que l'on construit  en symétrisant
en symétrisant  pour la multiplication (ou
pour la multiplication (ou  à partir de
à partir de  en symétrisant l'addition).
en symétrisant l'addition).Cette définition ne recouvre pas celle de division euclidienne, qui se pose de manière analogue mais dont le sens est radicalement différent.
Dans l'idée, elle sert aussi à inverser la multiplication (dans a, combien de fois b). Le problème de définition ne se pose plus, puisque
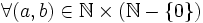 ,
, 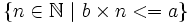 est une partie de
est une partie de  non vide et majorée, qui admet donc un plus grand élément.
non vide et majorée, qui admet donc un plus grand élément.Cette division, fondamentale en arithmétique, introduit la notion de reste. Néanmoins, comme pour toutes les divisions, le b de la définition ne peut être zéro, en effet, une division par 0 donnerait un résultat infini.
Propriétés
La division n'était pas à proprement parler une opération (loi de composition interne, définie partout), ses "propriétés" n'ont pas d'implications structurelles sur les ensembles de nombres, et doivent être comprises comme des propriétés des nombres en écriture fractionnaire.
"Non-propriétés"
- non-commutative car
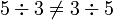
- non-associative car
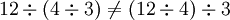
Remarques
- pseudo-élément neutre à droite : 1
- pseudo-élément absorbant à gauche : 0
- égalité de fractions
- de même dénominateur
- en général (qui découle de la construction de
 )
)
- de même dénominateur
- ordre
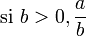 et
et 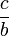 sont dans le même ordre que a et c
sont dans le même ordre que a et c
Algorithme de la division
Cet algorithme sert à déterminer une écriture décimale du quotient de deux nombres entiers, qui se généralise au quotient de deux nombres décimaux
Dans certains cas, la division "ne se termine pas", ce qui signifie que l'algorithme itère à l'infini.
Dans ce cas, le quotient est un rationnel non décimal, et on peut prouver que son développement décimal admet une période, dont la longueur est strictement inférieure au diviseur.
Dans une division non exacte a
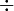 b (a et b étant deux nombres entiers, b non nul), si on note qp et rp respectivement le quotient et le reste obtenus après p en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité :
b (a et b étant deux nombres entiers, b non nul), si on note qp et rp respectivement le quotient et le reste obtenus après p en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité :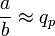 à 10 − p près ou
à 10 − p près ou 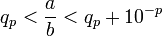
et 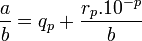
Un nombre irrationnel (réel, sans être rationnel) ne peut s'écrire sous forme de fraction, par définition.
Mathématiques et langue française
On peut diviser une entité en un nombre de parties dont l'addition donne cette entité, par un moyen implicite ou explicite.
Ainsi, on peut :
- diviser un gâteau en deux parts, par un coup de couteau
- simplement diviser un gâteau en deux [parts, par un moyen quelconque]
- diviser 1 en 2 demis, par la représentation mentale mathématique que l'on s'en fait
- simplement diviser 1 en 36ème
- etc.
On peut également diviser par dichotomie ou par malice, mais diviser par 2 est un concept mathématique.
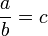 : « a divisé par b est égal à c ».
: « a divisé par b est égal à c ».Voir aussi
- Portail des mathématiques
Catégories : Opération | Divisibilité et factorisation
Wikimedia Foundation. 2010.

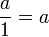
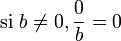
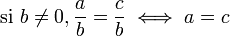
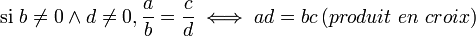

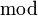

 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit