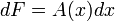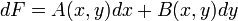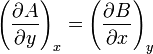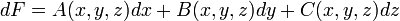- Differentielle exacte
-
Différentielle exacte
Une différentielle est dite exacte s'il existe une fonction dont elle dérive, c'est-à-dire s'il est possible de l'intégrer.
La différentielle ω définie sur un ouvert U est dite exacte s'il existe une fonction f différentiable sur U telle que : ω = df,.
Vue d'ensemble
En une dimension, une différentielle
est toujours exacte. En deux dimensions, d'après la réciproque du théorème de Poincaré, une différentielle
est exacte sur un ouvert simplement connexe U du plan R2, si et seulement si elle est fermée, c'est-à-dire qu'il existe entre A et B la relation:
En trois dimensions, une différentielle
est exacte sur un ouvert simplement connexe U de l'espace R3 s'il existe entre les fonctions A, B et C les relations:
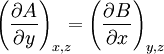 ;
; 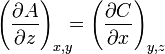 ;
; 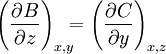
Ces conditions, qui sont faciles à généraliser, reposent sur l'indépendance de l'ordre de différenciation dans le calcul des dérivés secondes (théorème de Schwarz). Donc pour qu'une différentielle dF, qui est une fonction à quatre variables, soit une différentielle exacte, il y a six conditions à satisfaire.
En somme, quand une différentielle dF est exacte:
- la fonction F existe;
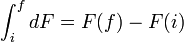
En thermodynamique, quand dF est exacte, la fonction F est une fonction d'état du système. Les fonctions thermodynamiques U, S, H, A et G sont fonctions d'état. Généralement ni le travail, W ni la chaleur, Q ne sont des fonctions d'état.
References
- Perrot, P. (1998). A to Z of Thermodynamics. New York: Oxford University Press.
- Zill, D. (1993). A First Course in Differential Equations, 5th Ed. Boston: PWS-Kent Publishing Company.
Liens externes
- Inexact Differential – from Wolfram MathWorld
- Exact and Inexact Differentials – University of Arizona
- Exact and Inexact Differentials – University of Texas
- Exact Differential – from Wolfram MathWorld
- Portail des mathématiques
Catégories : Équation différentielle | Thermodynamique
Wikimedia Foundation. 2010.