Construction des anneaux de polynômes

Construction des anneaux de polynômes

Construction de l'anneau des polynômes

En algèbre, l'anneau des polynômes formels (à une indéterminée) est un ensemble contenant des nombres, comme les entiers, les réels ou les complexes, et un objet supplémentaire, souvent noté X. Tous les éléments de l'anneau de polynômes s'additionnent et se multiplient : on trouve des polynômes comme 2X, X2 ou encore X2 - X - 1. De plus, une propriété importante est que les polynômes 1, X, X2, X3,... sont linéairement indépendants, aucune combinaison linéaire non triviale de ces polynômes n'est nulle. L'objet de cet article est de présenter une construction rigoureuse de cet ensemble et en particulier de l'objet X, appelé indéterminée.

Cette construction met en lumière les propriétés des éléments de cet ensemble, noté A[X], éléments qui sont appelés polynômes. On retrouve les propriétés qui caractérisent les nombres entiers, par exemple l'addition et la multiplication qui sont associatives et commutatives. Il existe un élément neutre pour l'addition et la multiplication des polynômes, mais si pour l'addition, tout polynôme possède un symétrique, tel n'est pas le cas pour la multiplication. L'élément X ne possède pas d'inverse, autrement dit 1/X n'est pas un polynôme.

L'ensemble des nombres, appelés coefficients, est noté A. Il peut être choisi comme l'un des ensembles de nombres cités ou encore comme n'importe quel anneau commutatif et unitaire (c'est-à-dire que la multiplication possède un élément neutre généralement noté 1). L'ensemble des coefficients des polynômes peut être, par exemple, constitué de polynômes ou d'éléments d'un corps fini.

Il existe d'autres constructions plus générales d'anneaux de polynômes, comme celles traitées dans Polynôme en plusieurs indéterminées ou dans Anneau non commutatif de polynômes.

Sommaire

Préambule

Éléments d'histoire

Le livre arithmetica de Diophante est le premier à décrire l'ajout d'une lettre à un ensemble de nombres.

L'idée d'associer une lettre à un ensemble de nombres date du IIIe siècle. Diophante définit la lettre S (la lettre grecque sigma) ainsi : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est S »[1]. Il ne travaille que sur les nombres entiers et les rationnels. Il définit les règles d'addition et de multiplication : « L'inverse de l'arithme multiplié par le bicarré de l'arithme donne le cube de l'arithme »[2], ce qui signifie que S4 est divisible par S et que le résultat vaut S3. Cette idée est petit à petit généralisée aux nombres irrationnels par la civilisation arabe, à l'origine de notre choix[3] de la lettre X. Si la construction est rudimentaire, elle permet aux mathématiciens de la Renaissance de résoudre toutes les équations jusqu'au degré 4, mais nous sommes cependant encore loin d'une construction rigoureuse, au sens de cet article.

Au XVIIe siècle apparaît un premier formalisme, celui des fonctions[4]. La variable x remplace la lettre X et le polynôme devient une fonction. Cet apport se traduit en résultats concrets, il permet de montrer le théorème de d'Alembert-Gauss qui assure l'existence d'autant de racines que le degré du polynôme, dans l'ensemble des nombres complexes.

Une question de Vandermonde, un mathématicien du XVIIIe siècle, finit par remettre à l'honneur le concept de polynôme formel, qui fait usage d'une lettre X qui s'additionne et se multiplie, mais qui n'est pas une fonction. Il cherche sans succès à résoudre l'équation cyclotomique à l'aide de radicaux[5], c'est-à-dire de nombres rationnels, de l'unité imaginaire i, des quatre opérations adjointes et des fonctions racine nièmes. C'est finalement Gauss qui y parvient[6] à l'aube du XIXe siècle. Pour cela il considère les polynômes, non comme des fonctions, mais comme des équivalents de nombres entiers, avec une division euclidienne, l'équivalent des nombres premiers et une décomposition unique en facteurs premiers. Il utilise pour cela des polynômes à coefficients dans les congruences, issues de l'arithmétique modulaire. Si les coefficients du polynôme sont choisis dans les congruences, les fonctions polynômes et les polynômes formels diffèrent. Et seul l'aspect formel permet de conclure dans ce cas particulier.

Ce n'est qu'au XXe siècle que le besoin de rigueur fait apparaître la construction présentée dans cet article.

Polynôme vu comme une suite

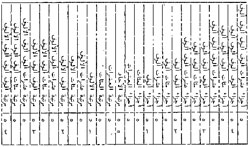Polynôme représenté par un tableau par al-Samaw'al

Il existe différentes méthodes pour représenter un polynôme[7], la plus classique est la suivante, illustrée sur deux polynômes exemples A et B :

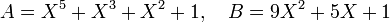
A = X^5 + X^3 + X^2 + 1,\quad B = 9X^2+5X+1

Cette écriture peut être rapprochée de celle de l'écriture décimale positionnelle des nombres 101101 et 951, qui peuvent se voir comme[8] :

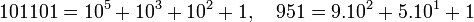
101101 = 10^5 + 10^3 + 10^2 + 1,\quad 951 = 9. 10^2 + 5.10^1 + 1

Comme l'addition et la multiplication des polynômes suivent presque les mêmes lois que celles des nombres, il peut être pratique, pour additionner et multiplier A et B de faire usage d'un tableau. C'est ainsi qu'al-Samaw'al, un mathématicien arabe du XIIe siècle représentent les polynômes, comme illustré sur la figure de gauche[9]. Sous forme de tableaux, et en utilisant les méthodes classiques d'addition et de multiplication sur les nombres, on obtient :

 +   X5   X4   X3   X2   X   1 
 A   1  0  1  1  0  1
 B   9  5  1
 A+B   1  0  1  10  5  2
 x   X7   X6   X5   X4   X3   X2   X   1 
 A   1  0  1  1  0  1
 B   9  5  1
 1  0  1  1  0  1
 5  0  5  5  0  5
 9  0  9  9  0  9
 AxB   9  5  10  14  6  10  5  1

Les lois de l'addition et de la multiplication sont presque les mêmes, la seule différence réside dans les retenues, qui n'existent pas avec les polynômes. Cette manière de voir un polynôme amène à l'usage d'une écriture condensée. Sous cette forme, un polynôme peut être vu comme une suite. Pour des raisons de commodité, il est plus simple de noter la suite à l'envers, c'est-à-dire en commençant par le coefficient de 1, puis celui de X etc... Avec ce système de notation :

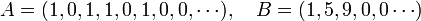
A = (1,0,1,1,0,1,0,0,\cdots),\quad B=(1,5,9,0,0 \cdots)

Ce système est à l'origine de la construction formelle des polynômes proposé ici.

Construction

A désigne un anneau (unitaire) commutatif.

Polynôme

Avec la logique du préambule, un polynôme est défini de la manière suivante :

Polynôme à une indéterminée à coefficients dans A — Un polynôme est une suite à valeurs dans A et nulle à partir d'un certain rang.[10]

Un polynôme P est ainsi, dans le cas général, une suite (p0, p1, p2,..., pk,...) d'éléments de A, que l'on note aussi (p k). Nulle à partir d'un certain rang signifie qu'il existe un entier N tel que si n est plus grand que N, alors pn est égal à 0.

L'ensemble de tous les polynômes ainsi défini est alors noté A[X].

On dispose d'une première propriété, correspondant à une tautologie de la définition :

Égalité entre deux polynômes — Deux polynômes sont égaux si, et seulement si, les suites de leurs coefficients sont égales.

Polynômes particuliers (monômes)

La suite nulle est appelée polynôme nul.

Un monôme est un polynôme dont tous les coefficients sont nuls, sauf, au plus, l'un d'entre eux. Un monôme non nul, correspondant à la suite nulle (0,0,...) sauf en un unique indice k, est appelé monôme de degré k. Cette seule valeur non nulle de la suite est appelée coefficient du monôme de degré k.

Le monôme (0,0,0,..., pk,0,0,...) de degré k est appelé monôme de degré k du polynôme (p0, p1, p2,..., pk,...). Le monôme non nul et de plus grand degré d'un polynôme est appelé monôme dominant et si le monôme dominant possède un coefficient égal à 1, le polynôme est dit unitaire.

Addition et multiplications

A l'image des ensembles de nombres, l'intérêt des polynômes réside dans l'existence d'une addition et d'une multiplication. Ces opérations correspondent à la description du préambule. De manière formelle, l'addition se définit par :

Addition des polynômes[11] — La somme de deux polynômes est égale à la suite dont la valeur indexée par k est la somme des deux coefficients des deux polynômes indexés par k.

\forall P,Q \in \mathbb A[X] \quad P = (p_0, p_1, p_2,\cdots, p_k,\cdots),\; Q = (q_0, q_1, q_2,\cdots, q_k,\cdots)
P+Q=(p_0+q_0, \quad p_1+q_1,\quad p_2+q_2,\quad\cdots,\quad p_k+q_k,\cdots)

Pour vérifier que la somme est bien définie, il faut s'assurer que la suite P + Q est bien nulle à partir d'un certain rang, Si la suite définissant P est nulle à partir du rang m et si celle définissant Q est nulle à partir du rang n, on remarque bien que la suite définissant P + Q est nulle à partir du rang le maximum de m et de n.

Il existe deux multiplications, la première est dite externe et correspond à la multiplication d'un nombre élément de A et d'un polynôme. Elle ressemble en cela à la multiplication d'un vecteur par un scalaire.

Multiplication scalaire[12] — La multiplication scalaire d'un élément a de A par un polynôme est la suite dont valeur indexée par k est le produit de a par le coefficient du polynôme indexé par k.

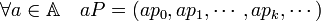
\forall a \in \mathbb A\quad aP = (ap_0,ap_1,\cdots,ap_k,\cdots)

De même que l'addition des polynômes correspond à l'addition des suites, la multiplication scalaire correspond à la multiplication scalaire des suites. Il est une fois encore aisé de vérifier que le résultat est encore une suite nulle, à partir d'un certain rang.

La deuxième multiplication correspond au produit de deux polynômes. Elle est calquée sur le produit décrit dans le préambule :

Produit de polynômes[13] — Soient P égal à (p k) et Q égal à (q l) deux polynômes à coefficients dans A, le produit P.Q est le polynôme défini par :

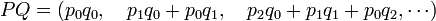
PQ=(p_0q_0,\quad p_1q_0+p_0q_1,\quad p_2q_0+p_1q_1+p_0q_2,\cdots)
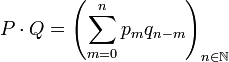
P\cdot Q =\left(\sum_{m=0}^n p_mq_{n-m}\right)_{n\in \mathbb N}

Une observation attentive montre que cette définition correspond exactement au calcul du préambule. Le coefficient d'indice 0 de A.B est le produit des coefficients d'indice 0 de A et de B. Le coefficient d'indice 1 de A.B est la somme de deux termes, le produit du coefficient d'indice 0 de A et du coefficient d'indice 1 de B pour le premier; le produit du coefficient d'indice 1 de A et du coefficient d'indice 0 de B pour le second. Une fois encore les deux définition concordent. Il en est de même pour tous les coefficients.

Vérifier que le produit est bien une suite nulle à partir d'un certain rang n'est pas très difficile. Si la suite P est nulle à partir du rang p, que la suite Q est nul à partir du rang q et que r est un entier plus grand que p + q, le coefficient d'indice r dans la suite P.Q est une somme de produits dont un (au moins) des facteurs est toujours nul, ce qui montre que le polynôme P.Q est une suite nulle à partir de l'indice p + q.

Indéterminée

On dispose de deux notations différentes pour les polynômes, soit à l'aide du symbole X, soit par les suites. Une unique définition permet de rendre ces deux notations cohérentes. Elle concerne l'objet symbolisé par la lettre X :

Indéterminée[14] — Le polynôme égal à la suite (0,1,0,0,...) nulle partout, sauf pour l'indice 1 où elle vaut 1, est appelée indéterminée et généralement notée X.

Avec cette définition, si n est un entier strictement positif, la suite nulle partout, sauf pour l'indice n où elle vaut 1, est égal à Xn, d'après la règle de multiplication de l'anneau. Pour généraliser cette propriété, on définit le polynôme X0 comme étant égal à la suite nulle partout, sauf pour l'indice 0 où elle vaut 1. Ce qui permet de disposer de la règle :

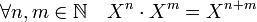
\forall n,m \in \mathbb N \quad X^n\cdot X^m = X^{n+m}

.

Considérons le polynôme A du préambule, il correspond à la suite (1,0,1,1,0,1,0,...), on peut l'écrire de la manière suivante :

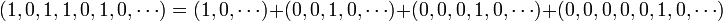
(1,0,1,1,0,1,0,\cdots )= (1,0,\cdots) + (0,0,1,0,\cdots) + (0,0,0,1,0,\cdots) + (0,0,0,0,0,1,0,\cdots)
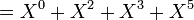
= X^0 + X^2 + X^3 + X^5\,

Dans le cas général, un polynôme P, égal à (p0, p1, p2,..., pn,0 ,...) s'écrit de manière équivalente :

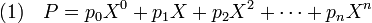
(1)\quad P = p_0X^0 + p_1X + p_2X^2 + \cdots + p_nX^n \,

Avec cette nouvelle définition, un monôme est un polynôme de la forme a.Xn, où a est un élément de A appelé coefficient du monôme et n un entier positif, appelé degré du monôme.

L'ensemble A[X] ressemble maintenant à celui couramment utilisé en mathématique et appelé anneau des polynômes. La lettre X symbolise maintenant un objet rigoureusement défini.

La définition de l'indéterminée diffère selon le contexte. On en trouve une plus générale dans l'article polynôme en plusieurs indéterminées. Si la définition de l'indéterminée pour les séries formelles est analogue à celle présentée ici, les analystes utilisent parfois une convention différente[15], l'indéterminée est la lettre X et selon les besoins, cette lettre désigne soit le polynôme formel décrit ici, soit la variable x qui transforme l'objet série formelle en une fonction analytique.

Polynômes constants

La notation (1), n'est pas totalement usuelle. En général, on ne trouve pas le facteur X 0 dans l'expression d'un polynôme[16]. Pour comprendre pourquoi il peut-être omis, il est nécessaire d'étudier l'application φ de A dans A[X], qui à « a » associe le polynôme « a.X0 ». Un peu de vocabulaire est utile :

Constante d'un polynôme[17] — La valeur du coefficient d'indice 0 d'un polynôme est appelé constante du polynôme et un polynôme composée d'un seul monôme de degré 0 est appelé polynôme constant.

L'application φ est ainsi une application de A dans l'ensemble des polynômes constants de A[X]. Elle possède de nombreuses propriétés, tout d'abord c'est une bijection, c'est-à-dire qu'à un élément de A est associé un unique polynôme constant par φ et à un polynôme constant il existe un unique élément de A d'image ce polynôme constant. Au sens ensembliste, A et les polynômes constants sont deux ensembles copie l'un de l'autre.

L'ensemble des polynômes constants muni de l'addition et de la multiplications des polynômes est un sous-anneau (unitaire) de l'anneau des polynômes. L'addition de A est transportée par l'application φ, c'est-à-dire :

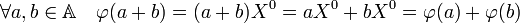
\forall a,b \in \mathbb A\quad \varphi(a+b) = (a+b)X^0 = aX^0 + bX^0 = \varphi(a) + \varphi(b)

Il en est de même pour la multiplication, ainsi les structures (A, +, .) et l'ensemble des polynômes constants muni des mêmes opérations, sont des copies l'une de l'autre. L'unité 1 de A est envoyée sur l'unité 1X0. On parle d'isomorphisme d'anneaux.

L'élément neutre 0 pour l'addition de A est aussi l'élément neutre de A[X] pour l'addition des polynômes, il en est de même pour l'élément neutre 1 de la multiplication de A. Enfin, la multiplication externe de a par un polynôme P donne le même résultat que le produit de a.X0 par le polynôme P.

Ces différentes raisons autorise à identifier A avec l'ensemble des polynômes constants. Cela revient à considérer que A[X] contient l'ensemble de nombre A et l'ensemble de nombres A est vu comme constitué des polynômes constants. Cette identification revient à dire que le polynôme X0 est égal à 1. On trouve maintenant exactement la notation habituelle :

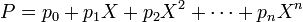
P = p_0 + p_1X + p_2X^2 + \cdots + p_nX^n \,

L'ensemble des polynômes A[X] correspond bien à celui décrit dans l'introduction, connu depuis Viète, le mathématicien du XVIe siècle qui utilise pour la première fois le terme de polynôme[18]. Sa construction est maintenant exposée rigoureusement.

Propriétés élémentaires

Une telle construction ne possède d'intérêt que si l'ensemble obtenu est riche en propriétés, ce qui est le cas. Ici ne présentées que les propriétés élémentaires de l'ensemble des polynômes, l'article polynôme formel synthétise les propriétés essentielles.

Structure d'anneau

Un ensemble de nombres, que ce soit celui des entiers, des rationnels, des réels ou des complexes, possède toujours des propriétés communes. Elles sont rassemblées pour décrire une structure générique, caractérisant la catégorie des anneaux commutatif unitaires et intègres.

L'addition des polynômes possède les propriétés suivantes :

Addition — L'ensemble des polynômes à coefficients dans A possède un élément neutre 0 pour l'addition, tout élément possède un opposé, l'addition est associative et commutative. Ces propriétés confèrent à l'ensemble des polynômes muni de l'addition une structure de groupe abélien.

Ces propriétés sont simples à établir. En fait, tout ensemble de suites à valeurs dans un groupe abélien possède une structure de groupe abélien.

La multiplication est un peu moins riche :

Multiplication — L'ensemble des polynômes à coefficients dans A possède un élément neutre 1 pour la multiplication, la multiplication est associative et commutative. Enfin, la multiplication est distributive sur l'addition.

La multiplication est un peu moins riche car tout élément non nul ne possède pas nécessairement un inverse, ainsi le polynôme X ne possède pas d'inverse. Ces différentes propriétés permettent d'établir :

Anneau[19] — L'ensemble A[X] des polynômes en une indéterminée et à coefficients dans A possède une structure d'anneau commutatif unitaire. Cet anneau est intègre si A est intègre : si P et Q sont des polynômes, P.Q est le polynôme nul si, et seulement si, P ou Q est nul.

Degré et valuation

Un indicateur important du polynôme est son degré :

Degré d'un polynôme[20] — Le degré d'un polynôme est le degré de son monôme dominant si le polynôme est non nul et moins l'infini sinon. Autrement dit, si le polynôme P (p0, p1, p2,..., pk,...) n'est pas nul, le degré est égal à l'entier n tel que pn soit le coefficient non nul d'indice le plus élevé :

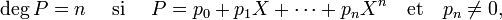
\deg P = n\quad\text{ si }\quad P = p_0 + p_1X + \cdots + p_nX^n\quad\text{et}\quad p_n \neq 0,

Si le polynôme est nul, on pose 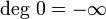\deg\, 0 = -\infty[21]. Parfois, on ne définit pas le degré du polynôme nul[22].

La définition de la somme et du produit des polynômes montre que :

Propriétés du degré — Si l'anneau A est intègre, le degré du produit de deux polynômes de degrés respectifs n et m est égal à la somme n + m. Le degré de la somme de deux polynômes de degrés respectifs n et m est inférieur ou égale au maximum de n et de m.

On remarque par exemple que le coefficients du monôme dominant du produit de deux polynômes non nuls est le produit des deux coefficients des monômes dominants des deux polynômes. Ce qui montre que si P et Q sont deux polynômes non nuls, P.Q est encore un polynôme non nul, autrement dit l'anneau A[X] est intègre. On remarque encore que le produit d'un polynôme non nul par X est toujours un polynôme de degré au moins 1, le polynôme X n'est donc pas inversible.

Valuation d'un polynôme[23] — La valuation d'un polynôme est le degré de son monôme non nul de plus petit degré, si le polynôme est non nul, et plus l'infini sinon. Autrement dit, si le polynôme P (p0, p1, p2,..., pk,...) n'est pas nul, la valuation est égale à l'entier m tel que pm soit le coefficient non nul d'indice le moins élevé :

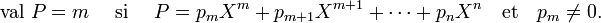
\text{val } P = m\quad\text{ si }\quad P = p_mX^m + p_{m+1}X^{m+1} + \cdots + p_nX^n\quad\text{et}\quad p_m \neq 0.\;

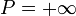Si le polynôme est nul, on pose val P = +\infty.

On dispose de propriétés équivalentes pour les valuations :

Propriétés de la valuation — Si l'anneau A est intègre, la valuation du produit de deux polynômes de valuations respectives n et m est égal à la somme n + m. La valuation de la somme de deux polynômes de valuation respectives n et m, est supérieure ou égale au minimum de n et de m.

Il existe en algèbre une définition de la valuation un peu différente et plus générale. La valuation spécifique définie dans ce paragraphe devient avec l'autre définition une valuation particulière.

Une des conséquences de ces deux applications, degré et valuation, est l'existence de deux divisions dans l'anneau des polynômes à coefficients dans un corps (c'est-à-dire si tous les éléments non nuls de A sont inversibles). L'une est dite "euclidienne" et l'autre "selon les puissances croissantes". Elles sont traitées dans l'article Division d'un polynôme.

Voir aussi

Notes

  1. ↑ La première inconnue par l'IREM de Poitier p 27.
  2. ↑ P. Ver Eecke Diophante d'Alexandrie. Les Six Livres Arithmétiques et le Livre des Nombres Polygones Desclée de Brouwer Liège (1926) p .2
  3. ↑ C. Kahn et O. Schladenhaufen mathématiques arabes au lycée Irem de Strasbourg, (1985).
  4. ↑ Amy Dahan-Dalmedico, Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986 (ISBN 2020092380) [détail des éditions], p 216.
  5. ↑ A. T. Vandermonde Mémoire sur la résolution des équations Mémoires de l'Académie des Sciences de Paris (1771).
  6. ↑ C. F. Gauss, Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Éd. Courcier (1807) pages 429-489.
  7. ↑ Serge Lang en propose plusieurs : Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  8. ↑ Ce rapprochement est proposé par : M. Delord Opérations arithmétiques et algèbre des polynômes Membre du (GRIP) groupe de réflexion interdisciplinaire sur les programmes
  9. ↑ Amy Dahan-Dalmedico, Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986 (ISBN 2020092380) [détail des éditions], p 91
  10. ↑ Cette définition est par exemple celle de (p97 dans l'édition anglaise) : Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  11. ↑ Cette définition est celle que propose en page 4, le site : J. M. Sarlat Introduction aux polynômes (2001)
  12. ↑ Cette définition est celle que propose en page 5, le site : J. M. Sarlat Introduction aux polynômes (2001)
  13. ↑ Cette définition est celle que propose en page 6, le site : J. M. Sarlat Introduction aux polynômes (2001)
  14. ↑ On trouve cette définition par exemple sur le site : M. Bercovier Polynôme par l'Université de Jussieu
  15. ↑ Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes [détail des éditions] page 9 (nouveau tirage juin 1985)
  16. ↑ On trouve le formalisme habituel, par exemple, dans le site : M. Bercovier Polynôme par l'Université de Jussieu
  17. ↑ On trouve cette définition, par exemple dans : M. Bercovier Polynôme par l'Université de Jussieu
  18. ↑ C. Florian A History of Mathematics New York The Macmillan Co 1919 p 139
  19. ↑ Voir, par exemple : R. Ferréol Polynôme Un cours de PCSI
  20. ↑ Degré d'un polynôme et d'une fraction rationnelle par Bibm@ath
  21. ↑ N. Bourbaki, Algèbre, chapitre IV
  22. ↑ C'est par exemple le choix de : M. Bercovier Polynôme par l'Université de Jussieu
  23. ↑ J. M. Sarlat Introduction aux polynômes (2001) p 12


Liens externes

Références

  • Amy Dahan-Dalmedico, Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986 (ISBN 2020092380) [détail des éditions]
  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Construction de l%27anneau des polyn%C3%B4mes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Construction des anneaux de polynômes de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Construction Des Anneaux De Polynômes — Anneau non commutatif de polynômes Le but de cet article est de montrer comment on obtient l anneau des polynômes à une variable (ou indéterminée) sur un anneau unitaire non nécessairement commutatif. Le cas des anneaux de polynômes à plusieurs… …   Wikipédia en Français

  • Construction des anneaux de polynomes — Anneau non commutatif de polynômes Le but de cet article est de montrer comment on obtient l anneau des polynômes à une variable (ou indéterminée) sur un anneau unitaire non nécessairement commutatif. Le cas des anneaux de polynômes à plusieurs… …   Wikipédia en Français

  • Construction anneaux de polynomes — Anneau non commutatif de polynômes Le but de cet article est de montrer comment on obtient l anneau des polynômes à une variable (ou indéterminée) sur un anneau unitaire non nécessairement commutatif. Le cas des anneaux de polynômes à plusieurs… …   Wikipédia en Français

  • POLYNÔMES — La théorie des équations et des polynômes a été le propos essentiel de l’algèbre jusqu’au XIXe siècle (cf. ÉQUATIONS ALGÉBRIQUES, ALGÈBRE) et est à la base de la théorie des corps et de la théorie des nombres algébriques. Nous nous sommes limités …   Encyclopédie Universelle

  • Catégorie des anneaux — Anneau (mathématiques) Pour les articles homonymes, voir Anneau. En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l addition et la multiplication des nombres. Sommaire… …   Wikipédia en Français

  • ANNEAUX COMMUTATIFS — Dans tout ce qui suit, on se bornera à considérer des anneaux commutatifs unitaires, c’est à dire possédant un élément unité pour la multiplication, noté 1. Les définitions sont celles de l’article suivant, ANNEAUX ET ALGÈBRES. De nombreux cas… …   Encyclopédie Universelle

  • Construction de l’anneau des polynômes — Construction de l anneau des polynômes En algèbre, l anneau des polynômes formels (à une indéterminée) est un ensemble contenant des nombres, comme les entiers, les réels ou les complexes, et un objet supplémentaire, souvent noté X. Tous les… …   Wikipédia en Français

  • Construction de l'anneau des polynômes — En algèbre, l anneau des polynômes formels (à une indéterminée) est un ensemble contenant des nombres, comme les entiers, les réels ou les complexes, et un objet supplémentaire, souvent noté X. Tous les éléments de l anneau de polynômes s… …   Wikipédia en Français

  • Anneau non commutatif de polynômes — Le but de cet article est de montrer comment on obtient l anneau des polynômes à une variable (ou indéterminée) sur un anneau (unitaire), non nécessairement commutatif. Le cas des anneaux de polynômes sur un anneau commutatif unifère est traité… …   Wikipédia en Français

  • Arithmétique des polynômes — En algèbre, l arithmétique des polynômes décrit les propriétés des polynômes qui peuvent se déduire de l arithmétique et qui sont un peu analogues à celles des nombres entiers. Par exemple, l anneau commutatif des polynômes K[X] à une… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”