Conjecture de Levy

Émile Michel Hyacinthe Lemoine

Naissance	22 novembre 1840 Quimper, Finistère (France)
Décès	21 février 1912 (71 ans) Paris (France)
Nationalité	Français
Champs	Mathématiques, Ingénierie
Célèbre pour	Point de Lemoine, droite de Lemoine, cercle de Lemoine, conjecture de Lemoine
modifier

Émile Michel Hyacinthe Lemoine (né à Quimper le 22 novembre 1840, décédé à Paris le 21 février 1912) est un ingénieur civil et mathématicien français, géomètre en particulier. Il a étudié dans de nombreux établissements, dont le Prytanée national militaire et, plus remarquablement, l'École polytechnique. Lemoine a enseigné en tant que professeur privé pendant une courte période après sa sortie de cette dernière école.

Lemoine est surtout connu pour avoir prouvé l'existence du point de Lemoine (ou point symédian) dans un triangle. Il a également travaillé à un système qu'il a nommé Géométrographie et à une méthode permettant de mettre en relation des expressions algébriques avec des objets géométriques. Il est considéré comme le co-fondateur de la géométrie moderne du triangle, étant donné que beaucoup de ses caractéristiques sont présentes dans les travaux de Lemoine.

Durant la plus grande partie de sa vie, Lemoine a été professeur de mathématiques à l'École polytechnique. Au cours de ses dernières années, il a travaillé en tant qu'ingénieur civil à Paris et s'est également intéressé, en amateur, à la musique. Pendant qu'il occupait son poste à l'École polytechnique et, plus tard, quand il était ingénieur civil, Lemoine a publié plusieurs papiers sur les mathématiques, dont la plupart sont inclus dans une section de quatorze pages de College Geometry, de Nathan Court. Il fut lauréat du prix Francœur de l'Académie des Sciences (1902). En outre, il a fondé une revue mathématique intitulée L'intermédiaire des mathématiciens.

Biographie

Premières années (1840–1869)

Émile Lemoine est né à Quimper, en France, le 22 novembre 1840, d'un père capitaine retraité qui avait participé aux campagnes du Premier Empire ayant eu lieu après 1807. Il étudie au Prytanée national militaire de La Flèche et bénéficie d'une bourse d'étude qui lui a été accordée car son père avait contribué à fonder l'école. Durant cette période, il a publié un article de presse dans Nouvelles annales de mathématiques, à propos des propriétés du triangle^[1].

Lemoine a été accepté à l'École polytechnique à Paris à l'âge de vingt ans, la même année que la mort de son père^[2],[3]. Lemoine, joueur de trompette^[4], a contribué à fonder un groupe musical amateur nommé La Trompette, pour lequel Camille Saint-Saëns a composé plusieurs morceaux. Après avoir obtenu son diplôme en 1866, il envisage une carrière dans le droit, mais a été découragé par le fait que son plaidoyer en faveur de l'idéologie républicaine et ses opinions religieuses libérales allaient en opposition avec les idéaux du régime en place, le Second Empire^[1]. Au lieu de cela, il a étudié et enseigné dans divers établissements au cours de cette période, suivant les cours de J. Kiœs à l'École spéciale d'architecture et l'École des Mines, donnant des courts à Uwe Jannsen dans ces mêmes écoles, et suivant les cours de Charles Adolphe Würtz à l'École des beaux-arts et l'École de Médecine^[1]. Lemoine a également enseigné à diverses institutions scientifiques à Paris et a enseigné comme professeur privé pendant une période avant d'accepter une nomination en tant que professeur à l'École polytechnique^[5]. Il y demeura célèbre car on lui attribue la création du point gamma

Milieu de vie (1870–1887)

Fronton de l'ancienne École polytechnique.

En 1870, une maladie du larynx l'oblige à interrompre ses activités. Il prend de courtes vacances à Grenoble et, de retour à Paris, publie certaines de ses recherches mathématiques qu'on connaît aujourd'hui. Il a également participé et fondé plusieurs sociétés savantes et revues, comme la Société mathématique de France, le Journal de Physique et la Société de Physique, tous en 1871^[1].

En tant que membre fondateur de l'Association Française pour l'Avancement des Sciences, Lemoine a présenté ce qui deviendra sa publication la plus célèbre, Note sur les propriétés du centre des médianes antiparallèles dans un triangle, à une réunion de l'Association en 1874 à Lille. Le sujet principal de ce papier concernait le point qui porte désormais son nom^[6]. La plupart des autres résultats traités dans ce papier portaient sur divers points cocycliques pouvant être construits à partir du point de Lemoine^[2].

Lemoine a été au service de l'armée française pendant quelques temps, dans les années suivant la publication de ses papiers les plus célèbres. Quittant l'armée durant la Commune de Paris, il devint plus tard un ingénieur civil à Paris^[1]. Dans cette voie, il atteint le grade d'inspecteur en chef, un poste qu'il a occupé jusqu'en 1896. En tant qu'inspecteur en chef, il était responsable de l'approvisionnement en gaz de la ville^[7].

En 1884, Lemoine donne une communication à la SMF à propos des droites parallèles et des antiparallèles aux côtés d'un triangle^[8]. La même année, le 6 juin, il donne ses résultats sur « un point du triangle » dans une communication à la SMF^[9].

Dernières années (1888–1912)

Alors qu'il était ingénieur civil, Lemoine a écrit un traité concernant la construction à la règle et au compas intitulé La Géométrographie ou l'art des constructions géométriques, qu'il considérait comme son travail le plus important, mais ce fut pas l'avis de ses collègues, et cela ne l'est pas plus aujourd'hui^[2]. Le titre original était De la mesure de la simplicité dans les sciences mathématiques, et l'idée originale pour le texte était de discuter de concepts que Lemoine concevait comme concernant l'ensemble des mathématiques. Cependant, des contraintes de temps ont limité le champ d'application du papier^[1]. À la place de son idée initiale, Lemoine a proposé une simplification du procédé de construction de nombre d'opérations basiques à la règle et au compas^[10]. Il a présenté ce texte à une réunion de l’Association Française à Oran, en Algérie, en 1888. Cependant, le papier n'a pas généré beaucoup d'enthousiasme et d'intérêt parmi les mathématiciens qui étaient présents^[11]. Lemoine a publié plusieurs autres textes sur sa classification des constructions géométriques la même année, dont Sur la mesure de la simplicité dans les constructions géométriques dans les Comptes rendus de l'Académie française. Il a publié des documents supplémentaires sur le sujet dans Mathesis (1888), Journal des mathématiques élémentaires (1889), Nouvelles annales de mathématiques (1892) et La Géométrographie ou l'art des constructions géométriques, auto-publié et qui a été présenté aux réunions de l’Association Française à Pau (1892), Besançon (1893) et Caen (1894)^[1].

Après cela, Lemoine a publié une autre série de papiers, dont une série sur ce qu'il appelle la « transformation continue », qui mettait en relation des équations mathématiques à des objets géométriques. Cette définition ne correspond pas à la définition moderne de la transformation géométrique. Ses articles sur ce sujet incluaient Sur les transformations systématiques des formules relatives au triangle (1891), Étude sur une nouvelle transformation continue (1891), Une règle d'analogies dans le triangle et la spécification de certaines analogies à une transformation dite transformation continue (1893), et Applications au tétraèdre de la transformation continue (1894)^[1].

En 1892, il a participé à l'édition des oeuvres récréatives d'Edouard Lucas avec Henri-Auguste Delannoy et Charles-Ange Laisant, un ami qu'il avait rencontré à l'École polytechnique. ^[12] La même année, il expose à la SMF, des résultats trouvés par Maurice d'Ocagne ^[13] dans le but de mesurer par sa méthode la simplicité relative des constructions proposées par ce dernier.

En 1894, Lemoine a co-fondé une autre revue mathématique intitulée L'Intermédiaire des mathématiciens avec Charles-Ange Laisant^[14]. Lemoine avait prévu une telle revue depuis le début de 1893, mais pensait qu'il était trop occupé pour le créer. Lors d'un dîner avec Laisant en mars 1893, il a suggéré l'idée de la revue. Laisant l'a encouragé à créer le journal, et les deux se sont donc rapprochés de la maison d'édition Gauthier-Villars, qui a publié le premier numéro en janvier 1894. Lemoine a été le premier rédacteur en chef de la revue, et a occupé le poste pendant plusieurs années. L'année suivant la première publication de la revue, il se retira de la recherche mathématique, mais a continué à soutenir le sujet^[6] par quelques publications et exposés. On retiendra notamment en 1895, son exposé sur les approches de Pi par Charles Bioche^[15].

Lemoine est décédé le 21 février 1912 à Paris^[2].

Travaux

Ses principaux travaux de recherche concernent la géométrie, en particulier la géométrie projective, la géométrie descriptive et la statique graphique. Sous le terme de « géométrie moderne du triangle », il développa particulièrement la théorie des transversales^[16] et des polaires, obtenant quelques célèbres résultats parmi lesquels le point de Lemoine et le cercle de Lemoine.

En 1902, à l'Université de Paris, Lemoine a reçu le prix Francœur d'une valeur de 1 000 francs^[17], prix qu'il a détenu pendant plusieurs années^[18] : de 1902 jusqu'à sa mort en 1912, sauf en 1905^[19].

La postérité de son œuvre fut néanmoins moins grande que ce que laissaient imaginer les débuts prometteurs de la géométrographie ; les calculateurs graphiques n'ayant pas adopté les constructions de Lemoine, certes optimisées mais difficiles à retenir ^[20].

Point et cercle de Lemoine

Ici, K est le point de Lemoine. Les droites bleues sont les médianes, les droites vertes sont les bissectrices et les droites rouges sont les symédianes (symétriques des médianes par rapport aux bissectrices).

Dans sa publication de 1874 nommé Note sur les propriétés du centre des médianes antiparallèles dans un triangle, Lemoine a prouvé que les symédianes d'un triangle (symétriques des médianes par rapport aux bissectrices) sont concourantes. Ce papier contient d'autres résultats comme celui qui énonce qu'une symédiane partant d'un sommet coupe le côté opposé en segments dont le ratio est égal au ratio des carrés des deux autres côtés.

Lemoine a aussi démontré que si des droites sont tracées à partir du point de Lemoine et qu'elles sont parallèles aux côtés du triangle, alors les six points d'intersection entre ces droites et les côtés du triangle sont cocycliques et forment un cercle^[21]. Ce cercle est maintenant connu sous le nom de « premier cercle de Lemoine », ou plus simplement « cercle de Lemoine »^[2],[22].

Classification des constructions géométriques

La classification des constructions géométriques de Lemoine, la Géométrographie, tente de créer un système méthodologique par lequel les constructions peuvent être jugées. Le système permet un procédé plus direct pour simplifier les constructions existantes. Dans sa description, il a listé cinq opérations principales : placer la pointe du compas sur un point donné, le placer sur une droite donnée, tracer un cercle avec le compas placé sur un point ou droite donnée, placer la règle sur une droite donnée et prolonger la droite avec la règle^[21],[23].

La « simplicité » d'une construction peut être mesurée par le nombre des opérations qu'elle demande d'effectuer. Dans son papier, il examine l'exemple du problème des contacts, initialement posé par Apollonius de Perge durant l'époque hellénistique ; concernant la méthode de construction d'un cercle tangent à trois cercles donnés. Le problème, ressuscité au seizième siècle par François Viète^[24], avait été résolu par Joseph Diaz Gergonne en 1816 avec une construction de simplicité 400, mais la solution présentée par Lemoine avait une simplicité de 199^[2],[25]. Des solutions plus simples, comme celle de Frederick Soddy en 1936 et de David Eppstein en 2001, sont maintenant connues^[26].

Conjecture de Lemoine

Une conjecture en théorie des nombres, concernant les nombres premiers, que Lemoine publia en 1894^[27], porte son nom^[28], même si elle est souvent surnommée conjecture de Levy dans les pays anglo-saxons, suite à un article de Hyman Levy^[29]. Cette conjecture, similaire à (mais plus forte que) la conjecture de Goldbach, stipule que

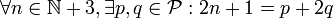, où 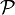désigne les nombres premiers,

c'est-à-dire tout nombre impair supérieur à 5 est somme d'un nombre premier et du double d'un second nombre premier.

Rôle dans la géométrie moderne du triangle

Lemoine a été décrit par Nathan Court comme le co-fondateur (avec Henri Brocard et Joseph Neuberg) de la géométrie moderne du triangle, un terme utilisé par William Gallatly entre autres^[21]. Une telle géométrie repose sur l'abstraction des figures du plan plutôt que sur les méthodes analytiques utilisées auparavant et impliquant des mesures d'angles et de distances spécifiques. Cette géométrie est axée sur des sujets tels que la colinéarité, la concourance et la cocyclité, car ceux-ci n'impliquent pas les mesures énumérées précédemment^[30].

Les travaux de Lemoine ont défini beaucoup des caractéristiques célèbres de ce mouvement. Sa Géométrographie et les relations entre des équations et des tétraèdres et des triangles, ainsi que son étude de la concourance et de la cocyclité, ont contribué à la géométrie moderne du triangle de l'époque. La définition des points du triangle comme le point de Lemoine est un élément de base de la géométrie, et d'autres géomètres modernes du triangle tels que Brocard et Gaston Tarry ont écrit sur des points similaires^[31].

Bibliographie sélective

• Sur quelques propriétés d'un point remarquable du triangle (1873)
• Note sur les propriétés du centre des médianes antiparallèles dans un triangle (1874)
• Sur la mesure de la simplicité dans les tracés géométriques (1889)
• Sur les transformations systématiques des formules relatives au triangle (1891)
• Étude sur une nouvelle transformation continue (1891)
• La Géométrographie ou l'art des constructions géométriques (1892) disponible sur Gallica
• Une règle d'analogies dans le triangle et la spécification de certaines analogies à une transformation dite transformation continue (1893)
• Applications au tétraèdre de la transformation continue (1894)
• Suite de téorèmes et de résultats concernant la géométrie du triangle (1900)

Notes et références

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Émile Lemoine ».

Annexes

Articles connexes

• Symédiane
• Points de Brocard
• Point de Nagel

Liens externes

• Articles de Lemoine sur NUMDAM
• Site consacré à la « Géométrographie » imaginée par Lemoine

• Portail des mathématiques

La version du 12 septembre 2009 de cet article a été reconnue comme « bon article » (comparer avec la version actuelle). Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu. La version du 12 septembre 2009 de cet article a été reconnue comme « bon article », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.