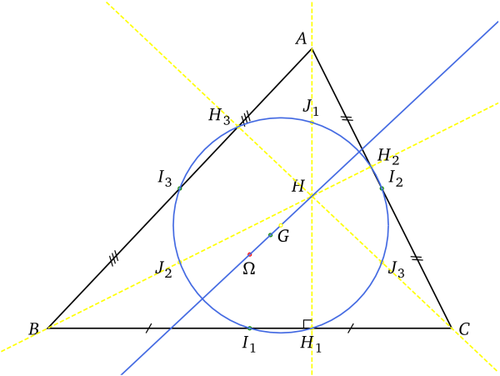
Cercle des neuf points

Cercle d'Euler

Cercle et droite d'Euler d'un triangle

En géométrie, le cercle d'Euler d'un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l'unique cercle passant par les neuf points remarquables suivants :

Les trois milieux des trois côtés du triangle ;
Le pied de chacune des trois hauteurs du triangle ;
Le milieu de chacun des trois segments reliant l'orthocentre à un sommet du triangle.

Sommaire

1 Définition et propriétés élémentaires
2 Indications
- 2.1 L'homothétie de centre G
- 2.2 L'homothétie de centre H
3 Découvertes
4 Quelques propriétés
5 Hexagramme de Pascal
6 Voir aussi

Définition et propriétés élémentaires

C'est le mathématicien Leonhard Euler qui a remarqué le premier que dans un triangle quelconque ( $A B C$ ) le centre de gravité $G$ , le centre du cercle circonscrit $Ω$ et l'orthocentre $H$ sont alignés. (Précisément, l'homothétie de centre $G$ et de rapport 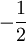$- \frac12$ transforme $H$ en $Ω$ .)

Indications

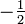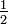Le cercle des neuf points d'Euler est l'homothétique du cercle circonscrit au triangle dans les homothéties de centre G et de rapport $- \textstyle\frac12$ et de centre H et de rapport $\textstyle\frac12$ .

L'homothétie de centre G permet de mettre en place la droite et le cercle d'Euler.

L'homothétie de centre H permet de trouver les neuf points du cercle d'Euler comme points correspondants du cercle circonscrit.

L'homothétie de centre G

Notons $I 1$ le milieu de $[B C]$ , $I 2$ le milieu de $[A C]$ et $I 3$ le milieu de $[A B]$ . Il n'est pas difficile de voir que cette même homothétie transforme le triangle $A B C$ en le triangle $I 1 I 2 I 3$ et le cercle circonscrit de $A B C$ en cercle circonscrit à $I 1 I 2 I 3$ : ce dernier cercle est précisément le cercle d'Euler.

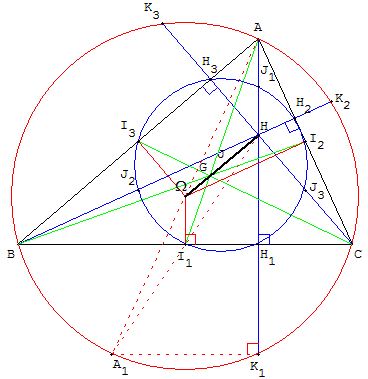
Les droites (I₁Ω) et (AH), perpendiculaires au côté [BC], sont parallèles. Soit A₁ le symétrique de A par rapport à Ω. Dans le triangle AHA₁, la droite (ΩI₁) passe par le milieu Ω du diamètre [AA₁] et est parallèle au côté (AH), c'est la droite des milieux du triangle. Le point I₁ est donc le milieu de [HA₁] : A₁ est le symétrique de H par rapport à I₁.

Les symétriques de l'orthocentre par rapport aux milieux des côtés du triangle sont situés sur le cercle circonscrit au triangle.

L'homothétie de centre H

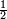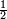L'homothétie de centre H et de rapport $\scriptstyle \frac12$ , transforme A₁ en I₁, de même les points I₂ et I₃ sont les images de deux points du cercle circonscrit. Le cercle d'Euler circonscrit au triangle I₁I₂I₃ est l'image du cercle circonscrit à ABC, dans l'homothétie de centre H et de rapport $\scriptstyle \frac12$ .

On note K₁, le point d'intersection (autre que A) de la hauteur (AH₁) avec le cercle circonscrit. Le segment [AA₁] étant un diamètre, le triangle AK₁A₁, inscrit dans un demi-cercle est rectangle. Les droites (BC) et (K₁A₁) , perpendiculaires à la hauteur (AH₁), sont parallèles. La droite (I₁H₁) passe par le milieu I₁ de [HA₁], c'est la droite des milieux de HA₁K₁, H₁ est donc milieu de [HK₁]. La droite (HK₁) étant perpendiculaire à (BC), K₁ est le symétrique de H par rapport à (BC).

Les symétriques de l'orthocentre par rapport aux côtés du triangle sont situés sur le cercle circonscrit au triangle.

Le point H₁ est le milieu de [HK₁], c'est donc l'image de K₁ par l'homothétie de centre H. Comme K₁ est situé sur le cercle circonscrit, H₁ est sur le cercle d'Euler. Les pieds des hauteurs sont situés sur le cercle d'Euler.

L'homothétie de centre H transforme les sommets du triangle en les milieux des segments [AH], [BH] et [CH] qui sont trois derniers points situés sur le cercle d'Euler

Découvertes

En 1821, les mathématiciens français Charles Julien Brianchon (19 décembre 1783 - 29 avril 1864) et Poncelet (1788-1867) démontrent ensemble que les milieux des côtés et les pieds des hauteurs du triangle sont cocycliques : ils mettent ainsi en évidence l'existence d'un cercle passant par ces six points remarquables. L'année suivante, le résultat fut redécouvert par le géomètre allemand Feuerbach (30 mai 1800 – 12 mars 1834). Le cercle d'Euler est aussi appelé cercle de Feuerbach. De plus, toujours en 1822, il démontra que le cercle des neuf points est tangent extérieurement aux cercles exinscrits et tangent intérieurement au cercle inscrit du triangle. Ce résultat s'appelle le théorème de Feuerbach et ajoute quatre nouveaux points remarquables : les points de tangence, appelés points de Feuerbach.

Par la suite, Olry Terquem (16 juin 1782 – 1862) mit en évidence que trois autres points appartiennent à ce cercle : les milieux des segments formés par les sommets du triangle et l'orthocentre. En 1842, Terquem apporta une deuxième preuve au théorème de Feuerbach. Une troisième preuve géométrique fut apportée en 1854.

Depuis, on lui a ajouté quelques dizaines d'autres points remarquables du triangle.

Quelques propriétés

On montre, en utilisant l'homothétie introduite au premier paragraphe, que :

Le rayon du cercle d'Euler est la moitié du rayon du cercle circonscrit.

Son centre, soit E, est sur la droite d'Euler, on a :

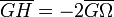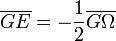
$\overline{GH} = -2 \overline{G\Omega}$ et $\overline{GE}=-{1\over 2}\overline{G\Omega}$

ce dont on déduit que dans un triangle, le centre du cercle d'Euler E, est le milieu de [HΩ], segment joignant l'orthocentre H au centre du cercle circonscrit Ω.

On déduit de ces relations que les points (Ω, E, G, H) sont en division harmonique :

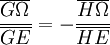
$\frac{\overline{G\Omega}}{\overline{GE}}= - \frac{\overline{H\Omega}}{\overline{HE}}$

Hexagramme de Pascal

Une propriété projective que n'avait pas vue Euler :

La droite de Pascal de l'hexagramme

H 1 I 2 H 3 I 1 H 2 I 3 H 1

est la droite d'Euler du triangle.

Voir aussi

Portail de la géométrie

Ce document provient de « Cercle d%27Euler ».

Catégories : Géométrie du triangle | Cercle et sphère

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cercle des neuf points de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Cercle Des Neuf Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle Des Neufs Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle des neufs points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle d'Euler — Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points remarquables… … Wikipédia en Français
cercle d'Euler — ● cercle d Euler Cercle (C) qui, pour un triangle donné, contient les milieux des côtés, les pieds des hauteurs et les milieux des segments joignant l orthocentre à chacun des sommets du triangle. ● cercle d Euler (synonymes) Cercle (C ) qui,… … Encyclopédie Universelle
neuf — 1. neuf [ nɶf ] adj. numér. inv. et n. inv. • nof 1119; lat. novem I ♦ Adj. numér. card. Nombre entier naturel équivalant à huit plus un (9; IX). 1 ♦ (Avec l art. défini, désignant un groupe déterminé de neuf unités) Les neuf Muses. 2 ♦ (Avec ou… … Encyclopédie Universelle
cercle — [ sɛrkl ] n. m. • 1160 « objet circulaire »; lat. circulus, de circus « cercle » I ♦ 1 ♦ Courbe plane fermée dont tous les points sont à égale distance R (⇒ 1. rayon) d un centre. Circonférence d un cercle, égale à 2 π R. Diamètre d un cercle :… … Encyclopédie Universelle
DIDACTIQUE - La pédagogie des mathématiques — Par delà les polémiques auxquelles elles donnent lieu, les réformes qui sont intervenues depuis le milieu ou la fin de la décennie soixante dans l’enseignement – celui de la grammaire et des mathématiques, notamment – se présentaient moins comme… … Encyclopédie Universelle
Cercle Bruges KSV — Ne pas confondre avec le Club Bruges KV, un autre club de la ville de Bruges avec lequel le Cercle entretient une rivalité depuis sa création. Infobox club sportif Cercle Brugge K.S.V … Wikipédia en Français
cercle — (sèr kl ) s. m. 1° Surface plane limitée par une ligne courbe, dite circonférence, dont tous les points sont à égale distance du centre. Un cercle double ou triple d un autre. Les cercles sont entre eux comme les carrés de leurs diamètres.… … Dictionnaire de la Langue Française d'Émile Littré

Dictionnaires et Encyclopédies sur 'Academic'

Cercle des neuf points

Cercle d'Euler

Sommaire

Définition et propriétés élémentaires