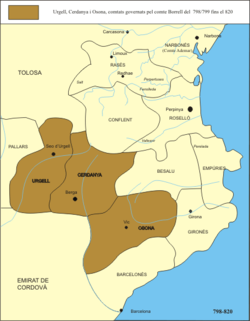
- Borell II
-
Borrell II
Fils de et Richilde, Borrell II est un comte de Barcelone mort en 992. Sous son règne, la Catalogne est devenue un état indépendant et a connu une renaissance qui préfigure la renaissance ottonienne.
Biographie
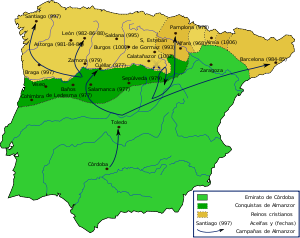Campagnes d'Al-mansur
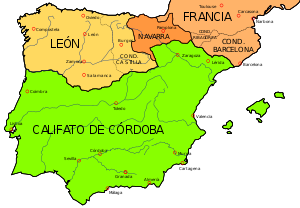Péninsule ibérique au Xe siècleSa date de naissance est inconnue. Il commence par gouverner les comtés de Barcelone et d'Urgell avec son frère Miron (948-966). En 966, la mort de son frère le laisse seul maître du comté de Barcelone.
A cette date, le Comté de Barcelone est culturellement le plus avancé du monde occidental : les bibliothèques espagnoles héritées du royaume wisigothique ont été enrichies par les connaissances des chrétiens mozarabes fuyant les persécutions d'Al-Mansur.
En 967, Borell II se rend dans le Rouergue pour épouser Ledgarde la fille du comte (qui est aussi Marquis de Gothie) et fait étape à Aurillac pour vénérer les reliques de Saint Géraud[1]. L'Abbé l'interroge sur le savoir des abbayes catalanes. Borell lui confirme l'excellence de ces monastères et l'abbé convainc le comte d'emmener Gerbert qui est particulièrement brillant y poursuivre sa formation[2]. Gerbert poursuit donc son instruction dans les abbayes catalanes de Vich et de Ripoll.[3] en 967, où il sera pris en charge par le savant évêque Hatton[4]. Le comte, étonné par les facultés intellectuelles de Gerbert d'Aurillac, le présente en 970 au pape Jean XIII et à l'empereur Othon Ier. Gerbert poursuit son ascension : il sera pape de 998 à 1002 sous le nom de Sylvestre II).
Borrell épouse en 968 Leutgarde, fille de Raymond III comte de Rouergue. Ils ont 6 enfants : Ramòn Borrell qui prendra sa suite à la tête du comté, Ermengaud 1er qui héritera du comté d'Urgell de son oncle Miron, Aldrie, Bonne, devenue abbesse de St Pierre de Barcelone, Ermengarde et Riquilde.
Après le sac de Barcelone par Al-Mansur en 985, Hugues Capet n'envoyant aucune aide, la Catalogne cesse de reconnaître sa suzeraineté. Elle s'émancipe définitivement du pouvoir royal, mais Borel II doit traiter avec Al-Mansur. Il fait reconstruire les fortifications de Barcelone avant de mourir en 992.
Le califat de Cordoue, miné par des guerres internes, a besoin de mercenaires et les catalans s'enrôlent massivement dans les armées d'Al-Mansour. En contrepartie, l'or musulman fait la fortune de la cité comtale, lui permettant enfin d'être la capitale de cette Catalogne naissante et, dès l'effondrement du califat (1009-1031), de dicter sa loi aux rois maures voisins de Tortose ou Lérida. Ces dissensions entrainent donc une période de stabilité propice à la Catalogne, qui connaît un important développement technique, démographique et culturel. Cette poussée culturelle se propage à l'Europe via les réseaux monastiques et les voies de pèlerinage (Saint-Jacques de Compostelle) et commerciales (Barcelone est un port ouvert sur la méditerranée).
Sources
- Philippe Conrad. Les origines de la Catalogne, de la marche d'Espagne carolingienne au comté de Barcelone, Clio.fr: [3]
- David Maso. Barcelone, ville des paradoxes, Clio.fr: [4]
Possessions territoriales de Borrell IINotes et références
Précédé par Borrell II Suivi par Sunyer Ier comte de Barcelone Raymond Borrell 
Portail des Pays catalans
Catégories : Comte de Barcelone | Reconquista | Naissance à Barcelone | Décès en 992 | Comte d'Urgell
Wikimedia Foundation. 2010.
