- Graphe de Fritsch
-
Graphe de Fritsch 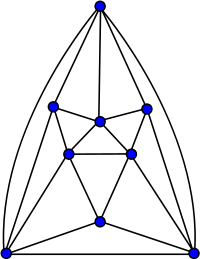
Représentation du graphe de Fritsch.Nombre de sommets 9 Nombre d'arêtes 21 Distribution des degrés 4 (3 sommets)
5 (6 sommets)Rayon 2 Diamètre 2 Maille 3 Automorphismes 12 Nombre chromatique 4 Indice chromatique 6 Propriétés Hamiltonien
Planairemodifier 
Le graphe de Fritsch est, en théorie des graphes, un graphe possédant 9 sommets et 21 arêtes.
Sommaire
Histoire
En 1879, Alfred Kempe publie une preuve du théorème des quatre couleurs, une des grandes conjectures de la théorie des graphes[1]. Bien que le théorème soit vrai, la démonstration de Kempe, basée sur les propriétés d'une chaine particulière, est erronée. Heawood le prouve en 1890[2] (avec le graphe 4-chromatique de Heawood comme exemple) et Vallée Poussin arrive au même résultat en 1896 (avec le graphe de Poussin comme exemple)[3].
Bien que la preuve de Kempe soit fausse, les chaines de Kempe restent utiles en théorie des graphes et les exemples la contredisant intéressent toujours les mathématiciens. Par la suite d'autres graphes contre-exemples furent donc exhibés : d'abord le graphe d'Errera en 1921[4],[5], puis le graphe de Kittell en 1935, avec 23 sommets[6].
Enfin deux contre-exemples minimaux sont construits : le graphe de Soifer, en 1997 est le premier découvert[7],[8]. Une année plus tard, le graphe de Fritsch, également d'ordre 9, est publié[9].
Propriétés
Propriétés générales
Le diamètre du graphe de Fritsch, l'excentricité maximale de ses sommets, est 2, son rayon, l'excentricité minimale de ses sommets, est 2 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 4-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 4 sommets ou de 4 arêtes.
Coloriage
Le nombre chromatique du graphe de Fritsch est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 3-coloration valide du graphe.
L'indice chromatique du graphe de Fritsch est 6. Il existe donc une 6-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes d'un graphe. Cela donne une fonction dépendant du nombre de couleurs autorisé. Cette fonction est polynomiale et est qualifiée de polynôme chromatique du graphe. Ce polynôme a pour racines tous les entiers positifs ou nuls strictement inférieurs à 4 et est de degrés 9. Il est égal à : (x − 3)(x − 2)(x − 1)x(x5 − 15x4 + 95x3 − 320x2 + 570x − 422).
Propriétés algébriques
Le groupe d'automorphismes du graphe de Fritsch est un groupe d'ordre 12 isomorphe au groupe diédral D6, le groupe des isométries du plan conservant un hexagone régulier. Ce groupe est constitué de 6 éléments correspondant aux rotations et de 6 autres correspondant aux réflexions.
Le polynôme caractéristique du graphe de Fritsch est : − (x − 1)(x + 2)2(x2 − 2)2(x2 − 3x − 8).
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Fritsch Graph (MathWorld)
Références
- Kempe, A. B. "On the Geographical Problem of Four-Colors." Amer. J. Math. 2, 193-200, 1879.
- P. J. Heawood, "Map colour theorem", Quart. J. Pure Appl. Math. 24 (1890), 332–338.
- R. A. Wilson, Graphs, colourings and the four-colour theorem, Oxford University Press, Oxford, 2002. MR 2003c:05095 Zbl 1007.05002.
- Errera, A. "Du coloriage des cartes et de quelques questions d'analysis situs." Ph.D. thesis. 1921.
- Peter Heinig. Proof that the Errera Graph is a narrow Kempe-Impasse. 2007.
- Kittell, I. "A Group of Operations on a Partially Colored Map." Bull. Amer. Math. Soc. 41, 407-413, 1935.
- A. Soifer, “Map coloring in the victorian age: problems and history”, Mathematics Competitions 10 (1997), 20–31.
- Gethner, E. and Springer, W. M. II. "How False Is Kempe's Proof of the Four-Color Theorem?" Congr. Numer. 164, 159-175, 2003.
- R. Fritsch and G. Fritsch, The Four-Color Theorem, Springer, New York, 1998. MR 99i:05079.
Wikimedia Foundation. 2010.
