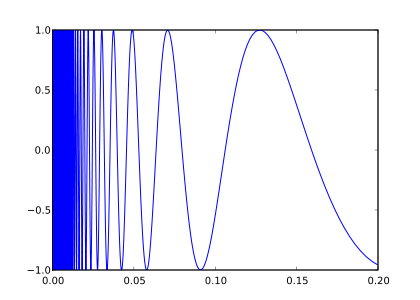
- Courbe sinus du topologiste
-
Dans le chapitre des mathématiques concernant la topologie, la courbe sinus du topologiste est un espace topologique avec plusieurs propriétés intéressantes qui en font un exemple important.
La courbe sinus du topologiste T est définie comme le graphe de la fonction sin(1/x) sur l'intervalle (0, 1], complété par un point à l'origine, muni de la topologie induite par celle du plan Euclidien.
Sommaire
Image de la courbe
Lorsque x approche de zéro, 1/x tend vers l'infini. Ainsi la fréquence de l'oscillation de la courbe croît sur la partie gauche du graphe.
Propriétés
La courbe sinus du topologiste T est connexe mais ni localement connexe ni connexe par arcs. C'est parce que l'ensemble contient le point (0,0) mais qu'il n'est pas possible de relier la fonction à l'origine ni de tracer un chemin.
T est l'image continue d'un espace localement compact (en effet, soit V l'espace {−1} ∪ (0, 1], et utiliser l'application f de V sur T définie par f(−1) = (0,0) and f(x) = (x, sin(1/x)) pour x > 0), mais n'est pas localement compact lui-même.
La dimension topologique de T est 1.
Variantes
Deux variantes de la courbe sinus du topologiste ont d'autres propriétés intéressantes.
La courbe sinus fermée du topologiste peut être définie en prenant la courbe sinus du topologiste et en ajoutant l'ensemble des points adhérents,
![\{(0,y)\mid y\in[-1,1]\}](3/2937b7c81fcfd7e39fae1226db96baad.png)
. Cet espace est fermé et borné et donc compact par le théorème de Borel-Lebesgue, mais a des propriétés similaires à la courbe sinus du topologiste — il est connexe mais ni localement connexe ni connexe par arcs.La courbe sinus prolongée du topologiste peut être définie en prenant la clôture topologique de T et en ajoutant l'ensemble
![\{(x,1) \mid x\in[0,1]\}](b/55b720ad562ea26780dea7ef22888b0a.png)
. Cet espace est connexe par arcs mais non localement connexe.Bibliographie
(en) Lynn Steen (en) et J. Arthur Seebach, Jr. (en), Counterexamples in Topology (en), Mineola, NY, Dover, 1995 (1re éd. 1978) (ISBN 978-0-486-68735-3), p. 137–138 MR{{{1}}}
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Topologist's sine curve » (voir la liste des auteurs)
Catégorie :- Espace topologique remarquable
Wikimedia Foundation. 2010.
