Espace Localement Connexe

Espace Localement Connexe: Espace localement connexe

L'espace vert A est connexe, alors que l'espace bleu B ne l'est pas

En mathématiques et plus particulièrement en topologie, un espace localement connexe est un espace dans lequel le voisinage de chaque point est constitué exclusivement d'ensembles connexes, c'est-à-dire d'ensembles faits d'une seule pièce et sans "trous".

Définition d'un espace localement connexe

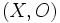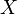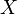Soit $(X,O) \,$ un espace topologique. On dit que $X \,$ est localement connexe si tout voisinage de tout point $x \,$ de $X \,$ contient un voisinage connexe de $x \,$ (pour la topologie induite par la topologie de $X \,$ ).

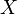Cela signifie que tout point de cet espace topologique admet une base de voisinages connexes.

La connexité locale n'est pas préservée par image continue.

Un espace topologique est localement connexe si et seulement si, pour tout ouvert 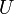$U \,$ , les composantes connexes de 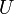$U \,$ sont ouvertes.

Exemples

Les exemples les plus classiques d'espace topologique localement connexes sont $\R$ , $\mathbb C$ , $\R^{n}$ ...

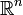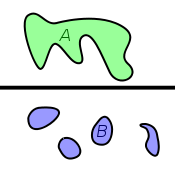
Un exemple d'espace connexe qui n'est pas localement connexe: dans 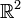$\mathbb{R}^{2}$ muni de la topologie usuelle on considère la partie 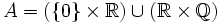$A=(\{0\} \times \mathbb{R}) \cup (\mathbb{R} \times \mathbb{Q})$ . Alors A est connexe mais n'est pas localement connexe. En particulier, tout point de A possède dans A un voisinage connexe (à savoir A lui-même) mais ne possède pas forcément de base de voisinages connexes.

Portail des mathématiques

Ce document provient de « Espace localement connexe ».

Catégorie : Topologie générale

Contenu soumis à la licence CC-BY-SA. Source : Article Espace Localement Connexe de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Espace localement connexe — Le « peigne » (en) est connexe, mais pas localement connexe. En mathématiques, plus précisément en topologie, un espace localement connexe est … Wikipédia en Français
Espace Localement Connexe Par Arcs — Définition d un espace localement connexe Soit un espace topologique. On dit que est localement connexe par arcs si tout voisinage de tout point de contient un voisinage connexe par arcs de … Wikipédia en Français
Espace localement connexe par arcs — En mathématiques, plus précisément en topologie, un espace localement connexe par arcs est un espace topologique possédant une base d ouverts dont chacun est connexe par arcs. Définition équivalente Un espace X est localement connexe par arcs si… … Wikipédia en Français
Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… … Wikipédia en Français
Espace simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Espace localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Localement compact — Espace localement compact En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de… … Wikipédia en Français
Espace Paracompact — Un espace topologique est dit paracompact si tout recouvrement ouvert admet un raffinement (ouvert) localement fini. Cette définition a été introduite par le mathématicien français Dieudonné. On rappelle qu un recouvrement (Xi) d un espace… … Wikipédia en Français
Espace semi-localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace Localement Connexe

Espace localement connexe

Définition d'un espace localement connexe

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Espace Localement Connexe

Espace localement connexe

Définition d'un espace localement connexe

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link