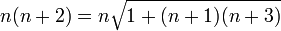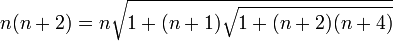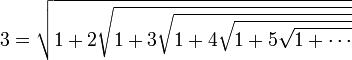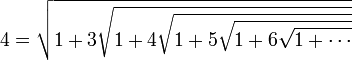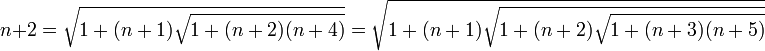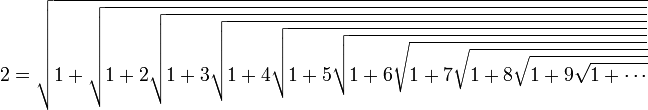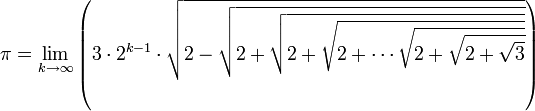- √
-
Racine carrée
La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note
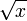 ou x½.
ou x½.Une tablette d'argile datée du XLVIIIe siècle av. J.-C. montre que les Babyloniens connaissaient la racine carrée de deux et un algorithme de calcul.
Tout nombre réel x positif possède une racine carrée qui est elle-même un nombre réel. La racine carrée d'un nombre entier n est soit un entier, soit un nombre irrationnel, c'est-à-dire qu'elle ne peut être exprimée par une fraction. Il semble que √2 fut le premier nombre irrationnel connu, et la démonstration de ce fait l'une des premières démonstrations par l'absurde.
À la renaissance, des mathématiciens ont été amenés à définir la racine carrée d'un nombre négatif, ce qui a conduit à l'avènement des nombres complexes. L'extraction d'une racine carrée était la cinquième « opération classique », elle est aussi perçue comme une fonction.
Histoire
Article détaillé : Histoire de la racine carrée.La plus ancienne racine carrée connue apparaît vers 1 700 av. J.-C. sur la tablette YBC 7289. Il s'agit de la représentation d'un carré avec, sur un côté, le nombre 30 et, le long de la diagonale, un valeur approchée de √2.
Pythagore professait que « tout est nombre ».
Racine carrée et autres structures
Si un ensemble E possède une multiplication, il peut être intéressant de se poser la question de savoir quand, pour un élément a de E, il existe un élément b tel que b2 est égal à a. Si E est égal à Z, a vérifie la propriété précédente si, et seulement si a est un carré parfait. Le terme de racine carrée sera étendu pour une raison de simplicité. La phrase 3 n'a pas de racine carrée dans Z possède un sens complètement défini.
Supposons que l'ensemble E soit égal à celui des nombres complexes, c'est à dire des nombres de la forme a + i.b où a et b sont des nombres réels et i l'unité imaginaire. L'unité imaginaire est un nombre dont le carré est égal à -1. Si α est un nombre complexe, alors il existe toujours un nombre complexe β tel que β2 soit égal à α. De plus, -β vérifie la même propriété. Il est fréquent de dire que β et -β sont les racines carrées de α, ce qui est tout de même plus commode que de dire que β et -β sont les racines de l'équation X2 - α = 0. On parle alors des[1] racines carrées de α.
Par extension, et quand il n'existe pas d'ambiguité, la locution racine carrée de α où α est un élément d'un ensemble E munis d'une multiplication signifie n'importe quel élément x solution de l'équation x2 = α. La notation √α est néanmoins souvent déconseillée[1], elle est associée à un élément précis et non pas un ensemble.
Dans le cas des nombres réels, c'est l'article qui permet de faire la différence. Un auteur parlant d'une racine carrée de 2, traite d'un des deux éléments √2 ou bien -√2. En revanche l'expression la racine carrée de deux évoque toujours la solution positive. Comme l'expression √2 est toujours positive et le terme fonction racine définie sur les réels positifs désigne toujours la valeur positive, on évite cette confusion dans les enseignements un peu élémentaires des mathématiques en ne faisant usage que de l'expression : la racine carrée, alors toujours positive.
Fonction réelle
L’application
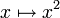 est une bijection
est une bijection 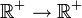 dont l’inverse est noté
dont l’inverse est noté 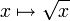 . Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de ses côtés.
. Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de ses côtés.Mise en garde : l’aire s’exprime dans le système universel en mètre carré et les longueurs en mètre. En prenant la racine carrée d’une quantité exprimée en mètres carrés, on obtient une quantité exprimée en mètres. Les physiciens attachent une importance particulière à l’analyse des unités ; cet aspect est effacé en mathématiques. Les nombres réels sont des constantes sans unité, et la racine carrée d’un nombre réel positif est un nombre réel positif.
Analyse
La fonction racine carrée vérifie les propriétés élémentaires suivantes valables pour tous nombres réels positifs x et y :
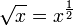
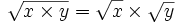
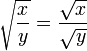 (sous la condition
(sous la condition 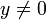 )
)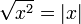 .
.
La fonction racine est continue en tout réel positif x (pour y proche de x,
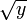 est proche de
est proche de 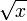 ). Mieux, cette fonction est 1/2-höldérienne. De plus, elle est dérivable en tout réel strictement positif x, mais elle n’est pas dérivable en x=0. En ce point, la pente de la tangente est infinie ; la courbe représentative admet en 0 une demi-tangente verticale.
). Mieux, cette fonction est 1/2-höldérienne. De plus, elle est dérivable en tout réel strictement positif x, mais elle n’est pas dérivable en x=0. En ce point, la pente de la tangente est infinie ; la courbe représentative admet en 0 une demi-tangente verticale.La fonction dérivée de
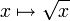 est donnée par :
est donnée par :La fonction racine est en réalité de classe
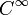 sur
sur 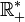 .
.Mieux encore, la fonction racine est développable en séries entières. Le développement en série de Taylor de la fonction racine carrée au point 1 s’obtient immédiatement à partir de la formule du binôme généralisée :
pour tout réel |h| < 1.
Construction géométrique de la racine carrée
La construction géométrique suivante se réalise à la règle et au compas et permet, étant donné un segment OB de longueur a, de construire un segment de longueur
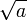 :
:- Construire le segment AB de longueur 1+a et contenant le point O avec AO = 1
- Construire le cercle C de diamètre AB.
- Construire la droite D perpendiculaire à (OB) et passant par O.
- Nommer H le point d’intersection du cercle C et de la droite D.
Le segment OH est de longueur
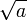 .
.La preuve consiste à appliquer le théorème de Pythagore :
- Au triangle rectangle HOB : OH2 + a2 = HB2
- Au triangle rectangle ABH : HB2 = (a+1)2 - AH2
- Au triangle rectangle AOH : AH2 = 12 + OH2
D’où OH2 + a2 = (a+1)2 - (12 + OH2), soit, après simplification OH2 = a, et donc
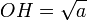 .
.Cette construction a son importance dans l’étude des nombres constructibles.
Notion algébrique générale
Soient x et a deux éléments d’un anneau A, tels que x2=a. L'élément x est alors une racine carrée de a. En général (notamment si l'anneau n'est pas intègre, ou s'il n'est pas commutatif), un élément peut avoir plus de deux racines carrées.
Les racines carrées de nombres complexes
Article détaillé : Racine de nombre complexe.La racine carrée sur
 est définie seulement pour les nombres positifs. Dans la résolution effective des équations polynomiales, l’introduction d’une racine carrée formelle d’un nombre négatif dans les calculs intermédiaires donnent des résultats exacts. C’est ainsi que le corps des nombres complexes a été introduit.
est définie seulement pour les nombres positifs. Dans la résolution effective des équations polynomiales, l’introduction d’une racine carrée formelle d’un nombre négatif dans les calculs intermédiaires donnent des résultats exacts. C’est ainsi que le corps des nombres complexes a été introduit.Pour tout nombre complexe non nul z, il existe exactement deux nombres complexes w tels que w2 = z. Pour des raisons de nature topologique, il est impossible de prolonger la fonction racine carrée
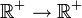 en une fonction continue
en une fonction continue 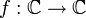 vérifiant f(z)2 = z.
vérifiant f(z)2 = z.On appelle détermination de la racine carrée sur un ouvert U de
 toute fonction continue
toute fonction continue 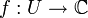 vérifiant f(z)2 = z.
vérifiant f(z)2 = z.La détermination principale de la racine carrée est la fonction
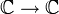 ainsi définie : si z s’écrit sous forme trigonométrique
ainsi définie : si z s’écrit sous forme trigonométrique 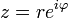 avec
avec 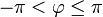 , alors on pose
, alors on pose 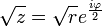 . Cette détermination principale n’est continue en aucun point de la demi-droite des réels strictement négatifs, et est holomorphe sur son complémentaire.
. Cette détermination principale n’est continue en aucun point de la demi-droite des réels strictement négatifs, et est holomorphe sur son complémentaire.Quand le nombre est dans sa forme algébrique, on a :
où le signe de la partie imaginaire de la racine est le même que le signe de la partie imaginaire du nombre initial (si elle est nulle, on prend par convention le signe +).
Notons qu’à cause de la nature discontinue de la détermination principale de la racine carrée dans le plan complexe, la relation
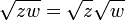 devient fausse en général.
devient fausse en général.Les racines carrées de matrices et d’opérateurs
Article détaillé : Racine carrée d'une matrice.Si A est une matrice symétrique définie positive ou un opérateur autoadjoint défini positif en dimension finie, alors il existe exactement une matrice symétrique définie positive ou un opérateur autoadjoint défini positif B tel que B2 = A. On pose alors : √A = B.
Plus généralement, pour toute matrice normale ou tout opérateur normal en dimension finie A, il existe des opérateurs normaux B tels que B2 = A. Cette propriété se généralise à tout opérateur borné normal sur un espace de Hilbert.
En général, il y a plusieurs tels opérateurs B pour chaque A et la fonction racine carrée ne peut pas être définie pour les opérateurs normaux d’une façon satisfaisante (continue par exemple). Les opérateurs définis positifs sont apparentés à des nombres réels positifs, et les opérateurs normaux sont apparentés à des nombres complexes. Les articles sur la théorie des opérateurs développent davantage ces aspects.
Extraction de racines carrées
Un premier algorithme
Nous allons exposer un algorithme qui va nous permettre d’extraire la racine carrée d’un nombre. Évidemment, si la racine carrée n’est pas un nombre décimal, alors l’algorithme ne se termine jamais, mais on s'approche autant qu'on peut le souhaiter du résultat : la suite des chiffres est exacte.
Nous commençons par séparer les chiffres du nombre par paires en commençant à partir de la virgule. Nous plaçons le nombre dont on veut extraire la racine en haut, de la même façon que lorsque nous effectuons une division selon la méthode classique ; la racine carrée sera inscrite au-dessus de ce nombre.
À chaque étape :
- on abaisse la paire de chiffres la plus significative non encore utilisée et on la place au côté d’un reste éventuel de l'étape précédente ;
- soit r le résultat intermédiaire de la racine carrée obtenu précédemment (égal à zéro au début). On cherche le plus grand chiffre x tel que le nombre y=(20r + x)x ne dépasse pas la valeur courante. On place ce nouveau chiffre x sur la ligne supérieure au-dessus de la paire abaissée ;
- on soustrait y de la valeur courante pour former un nouveau reste ;
- si le reste est nul et qu’il n’y a plus de chiffre à abaisser alors l’algorithme se termine sinon on recommence.
Exemple :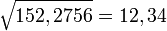
(nota : la suite des chiffres en gras s'inscrit au fur et à mesure au-dessus du nombre initial, au-dessus de la paire de chiffre traité selon l'algorithme, et donne le résultat : 12,34 . La place de la virgule est significative mais n'a pas besoin d'être prise en compte pendant les calculs, il suffit de la constater à la fin)
1 2 3 4 01 52,27 56 1 r=0 à cette étape x=1 01 1 y=(20*0+1)1 = 1 <= 01 alors que (20*0+2)*2 = 4 > 01 donc x = 1 ____ __ j'inscris le 1 : r=1 pour l'étape suivante 00 52 2x je pose 01-01=00 et j'abaisse 52 : apparait 52 x=2 00 44 12 y=(20*1+2)2 = 44 <= 52 alors que 20*1+3*3= 69 > 52 donc x = 2 _______ __ j'inscris le 2 : r=12 pour l'étape suivante, 20*r = 240 08 27 24x 52-44 = 08, je pose 08 et j'abaisse 27 : apparait 827 x=3 07 29 123 y=(20*12+3)*3 = 243*3 = 729 < 827 _______ __ j'inscris le 3 : r=123 pour l'étape suivante, 20*r=2460 98 56 246x 827-729 = 98, je pose 98 et j'abaisse 56 : apparait 9856 x=4 98 56 1234 y=(20*123+4)*4 = 9856 _______ j'inscris le 4 : r=1234 00 -- 9856-9856 = 0 et il n'y a plus rien à abaisser : fin de l’algorithmeVérification :
12,34 × 12,34 = 12×12 + 2×12×0,34 + 0,34×0,34. = 144 + 8,16 + (0,32×0,32 + 2×0,02×0,32 + 0,02×0,02) = 144 + 8,16 + 0,1024 + 0,0128 + 0,0004 = 152,2756
Jusqu’au XIXe siècle on utilisait couramment cet algorithme en accélérant les calculs à l’aide d’un abaque formée d’un jeu de réglettes : les bâtons de Napier.
Bien que décrite ici pour des nombres écrits en base 10, la procédure fonctionne dans n’importe quelle base, base 2 comprise. Dans ce qui précède, 20 représente le double de la base, et en binaire ce nombre serait remplacé par 100.
Par les fractions continues
Article détaillé : Fraction continue d'un nombre quadratique.Une fraction continue permet d'exprimer un nombre réel. Dans le cas particulier des racines carrés, son expression est relativement simple, ce qui permet de formuler deux méthodes d'extraction de racine. Elles possèdent toutes deux l'avantage de présenter des fractions optimales, c'est à dire que si p / q est une des valeurs que propose l'algorithme, alors aucune fraction de a / b avec b < q n'approche plus précisément la racine.
La deuxième méthode converge très rapidement, à chaque étape, le nombre de décimales exactes double.
La méthode de Héron
Article détaillé : Méthode de Héron.La méthode de Héron est un algorithme permettant d’approcher les racines carrées. Son importance est avant tout historique, elle a été développée par les Babyloniens. Elle fournit de bonnes approximations au prix de quelques divisions.
Exemple :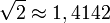
- Prenons la valeur rapprochée
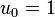 . On calcule de proche en proche :
. On calcule de proche en proche :
- On a ainsi obtenu la racine carrée de 2 à la précision 10 − 4.
On peut avoir une approche plus algorithmique en simplifiant cette méthode par la formule de Newton
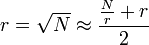 Même exemple :
Même exemple :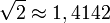
- Prenons de nouveau la valeur rapprochée
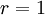 . On calcule de proche en proche :
. On calcule de proche en proche :
- On obtient la racine carrée de 2 à la précision 10 − 4.
- En appliquant cette formule on pourra écrire en langage basic :
- N = 2 /* Nombre dont on cherche la racine carrée
- r = 1 /* r = valeur rapprochée = 1
- DO /* Début de la boucle
- r = (r + (N / r)) / 2 /* Approximation
- PRINT "Racine de ";N;" ~= ";r /* Affichage du résultat
- LOOP /* Fin de la boucle
Calcul par la méthode du goutte à goutte
Article détaillé : Technique de l'extraction de racine.Les racines carrées, approximations entières
On a parfois besoin de construire des tables des parties entières des racines carrées des entiers naturels. Les premières sont données par :
CARRE 0 1 2 3 4 5 6 7 8 9 10 .. 15 16 17 .. 24 25 26 27 RACINE 0 1 1 1 2 2 2 2 2 3 3 .. 3 4 4 .. 4 5 5 5 Une observation des premiers termes montrent que la suite stationne d’entiers en entiers, et saute successivement d’un incrément de manière régulière. Plus précisément,
- le 0 est répété 1 fois,
- le 1, 3 fois
- le 2, 5 fois
- le 3, 7 fois
- le 4, 9 fois
Le nombre de fois que l’entier n est répété est le n-ième entier impair. La preuve repose sur l’identité suivante :
Autre méthode
Il est aisé de savoir quelle sera la taille de la racine carrée d'un nombre et cela avec un calcul élémentaire. Cela tient à la multiplication elle même: Si vous prenez le nombre de bits significatifs de deux nombres lorsque vous en faites le produit le résultat compte autant de bits que la somme des bits de chacun des opérandes. Dans le cas de la racine carrée les opérateurs sont égaux et comptent donc le même nombre de bits. En conséquence quand vous avez un nombre quelconque sa racine comporte la moitie de bits Si vous avez un nombre de 1024 bits vous savez que la racine en aura 512. Vous pouvez donc encadrer la racine ainsi 513 bits< Racine< 511 bits
Plus loin
Mais arrivé là on peut affiner considérablement le résultat Le prodigieux algorithme du compte goutte n’est utilisable que dans son intégralité car on ne connait en principe pas la longueur de la racine. C’est désormais faux. On peut donc utiliser ce calcul pour, par exemple, les 10 premiers chiffres de la racine et ensuite compléter la valeur a 512 bits Si vous voulez extraire la racine de : 286566083047005741820534465902668361736253328912991487181716 On commence par déduire la taille de la racine qui sera donc 30 chiffres, puis on extrait les 10 premiers chiffres au compte goutte 5389438444. nous complétons la racine avec 20 fois le chiffre 9 et nous obtenons ainsi la valeur haute de la racine 538943844499999999999999999999 et en complétant avec des 0 on obtient la limite basse 53894384440000000000000000000. Vérifions:la racine étant 538943844471945205222588086383 elle est bien comprise dans notre fourchette. Plus vous calculez de chiffres au ‘compte goutte’, qui est spécialement rapide, plus vous resserrez la fourchette
Précision: Comment passer de la fourchette au résultat. 538943844499999999999999999999 538943844400000000000000000000 = 538943844471945205222588086383 ????
La solution informatique est classique ! Une simple recherche dichotomique mais au lieu de tester directement la valeur calculée avec le nombre de départ il faut l'élever au carré
fonction Racine_64(C: int64): int64; var
a, b, d, d1: int64;
begin
A := borne basse B := borne haute repeat D := (a + B) shr 1; D1 := D * D; <= on élève au carré avant de tester if D1 > C then A := D - 1 else if C > D1 then B := D + 1 else Result := A; untel B > A;end;
Et à vous les racines carrées
Beaucoup Plus loin ?
La méthode présentée est parfaitement fonctionnelle et d'une efficacité remarquable. Elle souffre cependant de deux défauts 1- Il faut avoir implémenter la méthode du Goute a Goutte 2- Elle ne fonctionne que pour les racines carrées
Goute a goutte
Cette méthode est utilisée pour identifier les X premiers chiffres de la racine. Mais il existe d'autres méthodes. Cherchons la racine carrée de 700528656608304465974182053402668361736253328912991487181716 On prend les 19 premiers chiffres(19 correspondant a un nombre de 64 bits) et on en extrait la racine par la classique fonction SQRT de l' ordinateur 70052865660830446 et obtenez 264675018 exactement comme avec la méthode compte goutte mais sans l'utiliser Il ne vous reste qu' mettre des 9 ou des 1 comme dans l'exemple(un dessalage et un Or en informatique).On connait sans problème la longueur(voir plus fait)
les racines nième
La solution informatique est exactement la meme seul le test dans la recherche change D := (a + B) shr 1; D1 := D * D; <= on éleve au carré If suffit simplement de changer le Calcul de D1 par exponentiation désire Si vous cherchez la racine 164758 ème du nombre D1 := D * D; devient D1:=D^164758 et par approximations sucessives vous obtiendrez votre racine 164758 eme
Cette méthode présente une difficulté: si pour la racine carrée nous savons calculer rapidement la longueur (Nombre de bits div 2) Comment savoir quel sera la longueur de la racine 164758 Ce n'est en réalite sans importance et n'a quasiment aucune incidence sur le calcul Elle permet juste de gagner un ou deux cycles de la recherche dichotomie Quelques milliardièmes de secondes moyennant un calcul long informatiquement (conversion valeur ASCI et numérique) Si vous faites une recherche dichotomique pour 10 vous avez 1- 50 1- 25 1- 12 1- 6 2- 12 4- 12 8- 12 8- 12 Le calcul des racines par approximation a donc son couteau suisse: la recherche dichotomique
On peut si on le désire connaitre malgré tout la taille de la racine n° d'un nombre quelconque Sachant que pour connaitre le nombre de chiffres d'une exponentiation on utilise la formule suivante
R := Round(A * Log10(B)) + 1;
où A est la valeur et B la puissance. Il est aisé connaissant R et B de retrouver Log10(10] une simple recherche dichotomique (encore elle) vous permettra de retrouver le log10
Et les décimales?
Le calcul est automatique; il suffit de multiplier le nombre de départ par 10 autant de fois que vous désirez de décimales
C'est de la faute à Héron!
Bien involontaire, il faut le dire tout de suite. Dans la recherche dichotomique qu'il donne, il existe un goulet au niveau de la dichotomie elle même: le calcul du carré (pour lui une division). C'est la plus longue informatiquement parlant des quatre opérations. Son rapport avec ma multiplication est de 25. Il faut le même temps à un ordinateur pour faire 25 multiplications et divisions Toutes les recherches sur cette méthode étaient donc basées sur le gain de cycles de recherche et non sur le test lui meme.
Gagner un cycle de calcul chez Héron équivaut a en gagner 25 sur une recherche dichotomique niveau temps. On comprend l'incidence de la pertinence de la valeur d'initialisation.
Approximation de √a à l'aide de suites adjacentes
Soit a un nombre réel strictement positif.
Considérons les suites u et v définies par
- u(0) = 1,
- v(0) = a,
- u(n + 1) = la moyenne harmonique de u(n) et v(n) = 2 / (1 / u(n) + 1 / v(n)),
- v(n + 1) = la moyenne arithmétique de u(n) et v(n) = (u(n) + v(n)) / 2.
Les suites u(n) et v(n) sont adjacentes, et convergent vers la même limite :
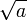 . L'erreur peut même être majorée par la différence v(n) − u(n).
. L'erreur peut même être majorée par la différence v(n) − u(n).Remarquons l'originalité de cette méthode qui mêle moyennes harmonique, géométrique et arithmétique. En effet
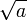 n'est autre que la moyenne géométrique de 1 et de a, et si on remplace u(0) par un réel strictement positif quelconque b, les suites u et v convergent vers la moyenne géométrique
n'est autre que la moyenne géométrique de 1 et de a, et si on remplace u(0) par un réel strictement positif quelconque b, les suites u et v convergent vers la moyenne géométrique 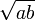 de a et b.
de a et b.(L'intéressante moyenne arithmético-géométrique et la moyenne géométrico-harmonique sont définies par des suites similaires.)
Curiosités
L’identité
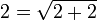 implique
implique 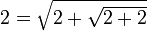 , et par itérations successives :
, et par itérations successives :Pour des raisons analogues, on obtient :
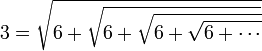 ;
; 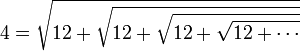 ; ...
; ...
Si r est un entier strictement supérieur à 1,
Plus généralement, si p étant un nombre réel supérieur ou égal à 1,
Si p est égal à 1, on obtient le nombre d'or:
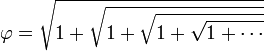 .
.
Le mathématicien Ramanujan obtint une formule alternative pour 3. Il partit de la décompositionet construisit le produit n(n + p) en fixant p = 2
Il substitua le terme (n + 3)
Ramanujan réitéra à l’infini en remplaçant maintenant n par 1 et obtint la jolie formule :
(bien entendu, il doit ensuite démontrer que le passage à la limite est légal)
En fixant n et p à d’autres valeurs positives ou en élevant au carré une formule obtenue, on peut également construire d’autres belles formules comme :
En résumé, la relation suivante, itérée à l’infini :
permet donc d’exprimer tous les nombres entiers strictement supérieurs à 1 comme une itération infinie de racines carrées.
En particulier, en fixant n = 0
(toutes ces formules sont en fait des affirmations sur des limites, qui se démontrent, de manière assez délicate, par encadrements)
Le nombre π s’exprime sous la forme d’une itération infinie de racines carrées :
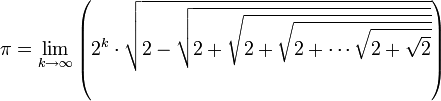 , où k est le nombre de racines carrées emboitées
, où k est le nombre de racines carrées emboitées
Ou encore :
Racines carrées des entiers de un à vingt
-
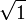
= 1 
≈ 1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462 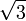
≈ 1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909 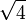
= 2 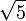
≈ 2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638 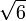
≈ 2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457 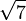
≈ 2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230 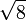
≈ 2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924 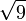
= 3 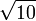
≈ 3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639 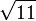
≈ 3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609 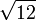
≈ 3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818 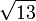
≈ 3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293 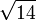
≈ 3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307 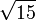
≈ 3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937 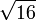
= 4 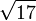
≈ 4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338 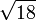
≈ 4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386 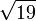
≈ 4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203 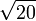
≈ 4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
Sources
- Smith D.E., History of Mathematics (livre 2)
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, seconde édition, Penguin Books, London, 2000, ISBN 0-691-00659-8
Références
- ↑ a et b Voir par exemple le site : racine carrée complexe par Homéomath
Voir aussi
- Racine carrée de deux
- Racine carrée de trois
- Racine carrée de cinq
- Racine cubique
- Racine de nombre complexe
- Nombre d’or
- Nombre irrationnel
- Nombre réel
- Exponentielle
Liens externes
- Portail des mathématiques
Catégorie : Racine carrée
Wikimedia Foundation. 2010.



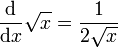
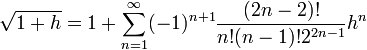
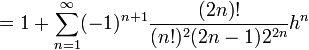
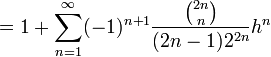
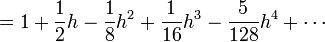

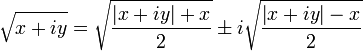
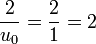
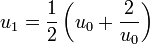
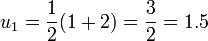
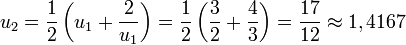
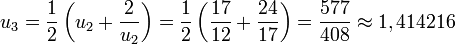
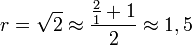
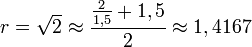
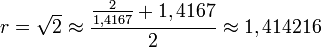
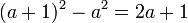
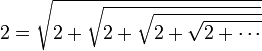
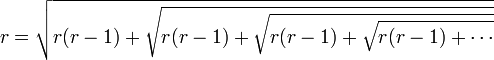
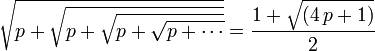
![(n+p)^2 = 1 + [n+(p-1)][n+(p+1)]\,](/pictures/frwiki/100/d2b6141735aa5e63c004c2334fdd055e.png)