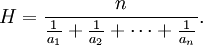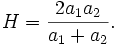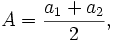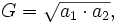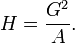Moyenne Harmonique

Moyenne Harmonique

Moyenne harmonique

La moyenne harmonique H de nombres réels positifs a1, ..., an est définie comme étant

H = \frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + \cdots + \frac{1}{a_n}}.

C'est donc l'inverse de la moyenne arithmétique de l'inverse des termes.

Sommaire

Exemples

Dans certains cas, la moyenne harmonique donne la véritable notion de "moyenne". Par exemple, si pour la moitié de la distance d'un trajet vous voyagez à 40 kilomètres par heure, et que pour l'autre moitié vous voyagez à 60 kilomètres par heure, votre vitesse moyenne est alors donnée par la moyenne harmonique de 40 et 60, ce qui donne 48. Votre temps de voyage total est donc le même que si vous aviez voyagé à 48 kilomètres par heure sur l'ensemble de la distance (attention toutefois, si vous aviez voyagé la moitié du temps à une vitesse, et l'autre moitié du temps à une autre vitesse, la moyenne arithmétique, dans ce cas 50 kilomètres par heure, vous aurait donné la bonne moyenne).

De même, si un circuit électrique a deux résistances reliées en parallèle, la première faisant 40 Ω et l'autre 60 Ω, la résistance moyenne des deux est 48 Ω ; la résistance totale du circuit est la même que si les deux résistances en parallèle étaient remplacées par des résistances de 48 Ω (attention, cette résistance moyenne n'est pas la résistance équivalente, qui est elle de 24 Ω, et qui correspond à remplacer les deux résistances en parallèle par une seule résistance de 24 Ω).

Moyenne harmonique de deux nombres

Article détaillé : moyenne harmonique pondérée.

Si l'on s'intéresse uniquement à deux nombres, il existe une fomule équivalente parfois plus pratique pour calculer la moyenne harmonique :

H = \frac {{2} {a_1} {a_2}} {{a_1} + {a_2}}.

Dans ce cas, leur moyenne harmonique est reliée à leur moyenne arithmétique,

A = \frac {{a_1} + {a_2}} {2},

et leur moyenne géométrique,

G = \sqrt {{a_1} \cdot {a_2}},

par la formule suivante :

H = \frac {G^2} {A}.

d'où

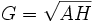G = \sqrt {{A} {H}} , i. e. la moyenne géométrique est la moyenne géométrique de la moyenne arithmétique et de la moyenne harmonique.

Ce résultat n'est valable qu'avec deux nombres.

Applications

  1. En dimensionnement mécanique, pour calculer le Rayon équivalent, de rayons de courbure, lors du contact entre 2 sphères.
 D'après la lois de Hertz-Boussinesq.


Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Moyenne harmonique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Moyenne Harmonique de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Moyenne harmonique — ● Moyenne harmonique inverse de la moyenne arithmétique des inverses des observations …   Encyclopédie Universelle

  • Moyenne harmonique — La moyenne harmonique H de nombres réels positifs a1, ..., an est définie comme étant C est donc l inverse de la moyenne arithmétique de l inverse des termes. Sommaire 1 Exemples 2 …   Wikipédia en Français

  • moyenne harmonique — harmoninis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. harmonic average; harmonic mean vok. harmonisches Mittel, n rus. среднее гармоническое, n… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • moyenne harmonique — harmoninis vidurkis statusas T sritis fizika atitikmenys: angl. harmonic average; harmonic mean vok. harmonisches Mittel, n rus. среднее гармоническое, n pranc. moyenne harmonique, f …   Fizikos terminų žodynas

  • Moyenne Harmonique Pondérée — En statistiques, si on considère le jeu de données suivant : X = { x1, x2, ..., xn} et les poids associés : W = { w1, w2, ..., wn} la moyenne harmonique pondérée se calcule de la manière suivante : Si tous les poids sont égaux, la… …   Wikipédia en Français

  • Moyenne harmonique ponderee — Moyenne harmonique pondérée En statistiques, si on considère le jeu de données suivant : X = { x1, x2, ..., xn} et les poids associés : W = { w1, w2, ..., wn} la moyenne harmonique pondérée se calcule de la manière suivante : Si… …   Wikipédia en Français

  • Moyenne harmonique pondérée — En statistiques, si on considère le jeu de données suivant : X = { x1, x2, ..., xn} et les poids associés : W = { w1, w2, ..., wn} la moyenne harmonique pondérée se calcule de la manière suivante : Si tous les poids sont égaux, la… …   Wikipédia en Français

  • Nombre à moyenne harmonique entière — Un nombre à moyenne harmonique entière est un nombre entier positif dont les diviseurs ont pour moyenne harmonique un nombre entier. Autrement dit, si a1, a2, ..., an sont les diviseurs du nombre, doit être un entier. Ces nombres ont été définis… …   Wikipédia en Français

  • Moyenne (mathématiques élémentaires) — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Moyenne générale — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”