- Équation de Planck
-
Loi de Planck
 Pour les articles homonymes, voir Planck.
Pour les articles homonymes, voir Planck.La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique.
La luminance[1] énergétique monochromatique est un flux énergétique par unité de surface, par unité d'angle solide et par unité de longueur d'onde ; elle s'exprime donc en W m-3.sr-1 en unités SI :
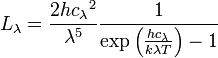
cλ = c / nλ est la vitesse du rayonnement électromagnétique dans le milieu où se propage le rayonnement, avec :
- nλ indice de réfraction du milieu pour la longueur d'onde λ
- c = 299 792 458 m/s (vitesse de la lumière dans le vide)
- h = 6,626 17×10-34 J.s (constante de Planck)
- k = 1,380 66×10-23 J/K (constante de Boltzmann)
- T est la température de la surface du corps noir en kelvin
Introduction
La loi de Planck décrit la répartition de l'énergie électromagnétique (ou la répartition de la densité de photons) rayonnée par un corps noir à une température donnée, en fonction de la longueur d'onde . La loi de Planck est présentée sous différentes variantes, qui emploient des grandeurs telle que l'intensité, la densité de flux ou bien la répartition spectrale. Toutes ces formes des différentes grandeurs de rayonnement sont des formes différentes de la loi de Plank.
A la fin du 19è siècle, les physiciens essayaient de comprendre le spectre du rayonnement des corps noirs en se fondant sur la physique classique, la physique statistique et l'électrodynamique classique. Des hypothèses contradictoires (loi de Wien, loi de Rayleigh-Jeans) et une concordance seulement partielle avec les résultats expérimentaux conduisirent à une situation non satisfaisante. C'est Max Planck qui, à la fin du siècle, réussit à trouver une loi de rayonnement complètement en accord avec les mesures expérimentales. Outre l'importance pratique du corps noir, la découverte de la loi de Planck en 1900 signe la naissance de la mécanique quantique : pour expliquer sa loi trouvée de manière empirique, Planck a du supposer que la lumière (et donc le rayonnement électromagnétique en général) n'était pas absorbée et émise de manière continue, mais uniquement de manière discrète, par l'intermédiaire de quanta (on parle aujourd'hui de photons).
D'après la loi du rayonnement de Kirchhoff, la capacité d'absorption et la capacité d'émission de rayonnement thermique d'un corps sont proportionnels pour toutes les longueurs d'ondes. Un corps noir est un corps hypothétique qui absorbe tout le rayonnement qu'il reçoit, quelle que soit la longueur d'onde. Comme sa capacité d'absorption prend la plus grande valeur possible quelle que soit la longueur d'onde, sa capacité d'émission prend également la plus grande valeur possible. Un corps réel ne peut pas émettre plus de rayonnement thermique qu'un corps noir, car celui-ci représente une source de rayonnement thermique idéale. Comme son spectre ne dépend d'aucun autre paramètre que de la température (en particulier, il ne dépend pas des propriétés du matériau), le corps noir est une source de référence utilisée dans de nombreux cas.
La loi de rayonnement de Planck
Comme la loi de Planck est valable dans de nombreux contextes différents, elle s'exprime sous différentes formes, toutes dérivées les unes des autres. Pour comprendre ces différentes formes de la loi de Planck, nous allons d'abord énoncer les grandeurs qui apparaissent dans les différentes formules.
Comme il est d'usage pour les grandeurs radiométriques, différentes grandeurs de rayonnement peuvent être utilisées pour décrire le spectre du rayonnement d'un corps noir. Les dénominations et symboles utilisés ici suivent la norme ISO 9288 (Août 1996). L'indice haut
 indique que la grandeur en question décrit spécifiquement les propriétés d'un corps noir. Les formules suivantes sont valables pour le rayonnement dans le vide. Pour le rayonnement dans un milieu d'indice de réfraction n, il faut remplacer les célérités dans le vide c par c/n et les longueurs d'onde λ par λ/n, sans modifier la fréquence ν.
indique que la grandeur en question décrit spécifiquement les propriétés d'un corps noir. Les formules suivantes sont valables pour le rayonnement dans le vide. Pour le rayonnement dans un milieu d'indice de réfraction n, il faut remplacer les célérités dans le vide c par c/n et les longueurs d'onde λ par λ/n, sans modifier la fréquence ν.On différencie
- les grandeurs spectrales, qui décrivent la dépendance à la fréquence (ou à la longueur d'onde) de manière explicite,
- les grandeurs totales, intégrées sur l'ensemble des fréquences (ou des longueurs d'onde)
ainsi que
- les grandeurs directionnelles, qui décrivent la dépendance à la direction de manière explicite,
- les grandeurs hémisphériques, intégrées sur toutes les directions du demi-espace.
Luminance energétique monochromatique
La luminance énergétique monochromatique
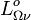 d'un corps noir à la température absolue T vaut
d'un corps noir à la température absolue T vaut- Selon la fréquence :
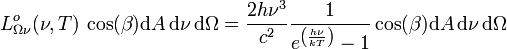
Unité SI de
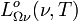 : W m-2 Hz-1 sr-1,
: W m-2 Hz-1 sr-1,- Selon la longueur d'onde :
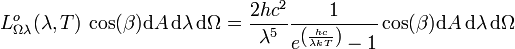
Unité SI de
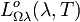 : W m-2 µm-1 sr-1.
: W m-2 µm-1 sr-1.
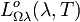 est la puissance rayonnée par un élément de surface dA dans le domaine de fréquences entre ν et ν+dν, dans l'élement d'angle solide dΩ délimité par les angles azimutaux φ et φ+dφ ainsi que les angles d'ascension polaires β et β+dβ. h est la constante de Planck, c est la célérité de la lumière dans le vide et k est le constante de Boltzmann. Le facteur cos(β) prend en compte le fait que, pour le rayonnement dans une direction indiquée par φ et β, seule la projection orthogonale à cette direction cos(β)dA de la surface dA est prise en compte comme surface rayonnante effective.
est la puissance rayonnée par un élément de surface dA dans le domaine de fréquences entre ν et ν+dν, dans l'élement d'angle solide dΩ délimité par les angles azimutaux φ et φ+dφ ainsi que les angles d'ascension polaires β et β+dβ. h est la constante de Planck, c est la célérité de la lumière dans le vide et k est le constante de Boltzmann. Le facteur cos(β) prend en compte le fait que, pour le rayonnement dans une direction indiquée par φ et β, seule la projection orthogonale à cette direction cos(β)dA de la surface dA est prise en compte comme surface rayonnante effective.La luminance énergétique monochromatique
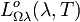 doit être indépendante de la direction pour des raisons thermodynamiques[2].
doit être indépendante de la direction pour des raisons thermodynamiques[2].Le corps noir rayonne de manière totalement diffuse, et suit le modèle du rayonnement de Lambert.
Lors du passage entre représentation fréquentielle et représentation en longueur d'onde, comme
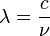 , on a les relations :
, on a les relations :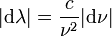 et
et 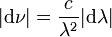
La luminance énergétique monochromatique est, comme son nom l'indique, une grandeur spectrale.
Exitance energétique monochromatique
En intégrant la luminance énergétique monochromatique suivant toutes les directions du demi-espace dans lequel rayonne l'élément de surface étudié, on obtient l'exitance[3] energétique monochromatique
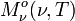 . Il vient :
. Il vient :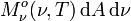
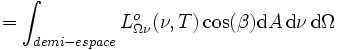
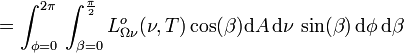
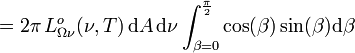
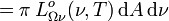 ,
,soit :
- Selon la fréquence
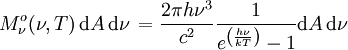
Unité SI de
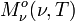 : W m-2 Hz-1
: W m-2 Hz-1- Selon la longueur d'onde
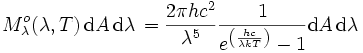
Unité SI de
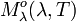 : W m-2 μm-1.
: W m-2 μm-1.
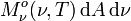 est la puissance rayonnée par l'élément de surface dA dans le domaine de fréquences entre ν et ν+dν dans le demi-espace. L'exitance énergétique monochromatique est une grandeur spectrale hémisphérique.
est la puissance rayonnée par l'élément de surface dA dans le domaine de fréquences entre ν et ν+dν dans le demi-espace. L'exitance énergétique monochromatique est une grandeur spectrale hémisphérique.Luminance énergétique
En intégrant la luminance énergétique monochromatique non pas sur les directions mais sur les fréquences, on obtient la luminance énergétique (totale)
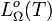 , telle que :
, telle que :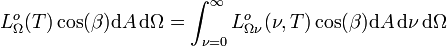
Comme
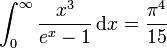 , le calcul de l'intégrale donne :
, le calcul de l'intégrale donne :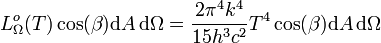
Unité SI de
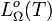 : W m-2 sr-1.
: W m-2 sr-1.
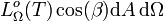 est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans l'angle solide dans la direction donnée par β.
est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans l'angle solide dans la direction donnée par β.La luminance énergétique est une grandeur totale directionnelle.
Exitance énergétique, densité de flux radiatif, loi de Stefan-Boltzmann
(voir l'article Loi de Stefan-Boltzmann)
En intégrant l'exitance énergétique monochromatique sur toutes les fréquences ou bien la luminance énergétique sur toutes les directions du demi-espace, on obtient l'exitance énergétique (ou densité de flux radiatif) Mo(T), telle que :
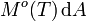
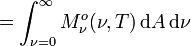
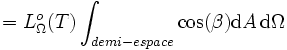
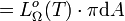
soit
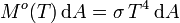
Unité SI de Mo(T) : W m-2,
avec la constante de Stefan-Boltzmann
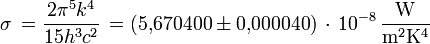 (CODATA[4] 2000).
(CODATA[4] 2000).Pour le rayonnement dans un milieu d'indice de réfraction n, la célérité de la lumière c doit être remplacée par c/n. L'exitance energétique augmente donc d'un facteur n2.
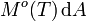 est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans le demi-espace.
est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans le demi-espace.L'exitance énergétique est une grandeur totale hémisphérique.
Flux radiatif
En intégrant l'exitance énergétique (densité de flux radiatif), sur l'ensemble de la surface rayonnante A, on obtient le flux radiatif (ou puissance rayonnée) de cette surface Φo(T), pour laquelle :
 ,
,soit
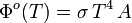
Unité SI de Φo(T) : W.
Φo(T) est la puissance rayonnée par l'ensemble de la surface A sur toutes les fréquences et dans le demi-espace tout entier.Densité spectrale d'énergie du rayonnement d'une cavité à rayonnement isotrope
Considérons une cavité fermée, dont les parois sont composées d'un matériau quelconque, et maintenu à la température T. A l'équilibre thermique, la cavité est emplie d'un rayonnement thermique isotrope, dont les caractéristiques ne dépendent que de la température T, et qui a donc un caractère universel.
En insérant un corps noir dans cette cavité, le rayonnement de la cavité doit redevenir identique après avoir atteint l'équilibre thermique, puisque le rayonnement ne dépend que de la température T. Comme le corps noir absorbe une certaine quantité de rayonnement et doit en réémettre la même quantité au même moment pour garantir l'équilibre, les luminances énergétiques spectrales de la cavité et le rayonnement du corps noir doivent être identiques. Les expression des grandeurs obtenues ci-dessus sont donc également valables pour le rayonnement de la cavité, et celui-ci a une énergie volumique de rayonnement constante, comme nous allons le voir.
Considérons une calotte sphérique emplie d'un rayonnement de corps creux dû à la température T. Comme les grandeurs de rayonnement sont les mêmes que pour le rayonnement du corps noir, la puissance incidente sur un élément de surface dA au centre du disque sur lequel repose la calotte, provenant de l'ensemble de la calotte sphérique, et dans le domaine de fréquences de ν à ν+dν, est donnée par la formule de l'exitance énergétique spectrale :
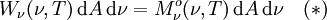
Soit
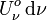 la densité d'énergie dans l'intervalle de fréquences de ν à ν+dν, et
la densité d'énergie dans l'intervalle de fréquences de ν à ν+dν, et 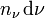 la densité de photons dans le même intervalle de fréquences :
la densité de photons dans le même intervalle de fréquences :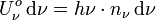
Comme le rayonnement est isotrope, la quantité de photons provenant de l'angle solide dΩ (donc de directions entre φ et φ+dφ et entre β et β+dβ) est donnée par le rapport de dΩ à l'angle solide de l'espace tout entier 4π. La densité de photons de fréquence entre ν et ν+dν provenant de l'angle solide dΩ est donc :
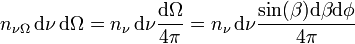
Parmi tous les photons de l'intervalle dν provenant de la direction dΩ, certains atteignent une surface dA se trouvant dans un cylindre penché β d'un angle dans la direction de dΩ et de surface de base dA. Par unité de temps dt, les photons qui traversent dA sont ceux qui se trouvent dans le cylindre de longueur cdt. Ils traversent donc dA avec un taux :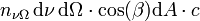
Comme chaque photon a une énergié hν, l'énergie traversant dA par unité de temps vaut :
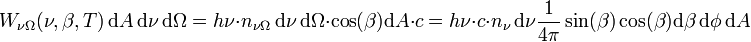
Des photons provenant de l'ensemble de la calotte sphérique traversent dA. L'intégration sur l'ensemble du demi-espace donne :
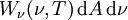
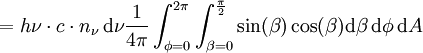
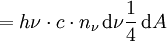
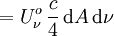
La comparaison avec ( * ) fait apparaître la relation :
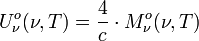
On a donc :
- Selon la fréquence :
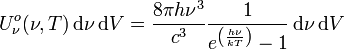
Unité SI de
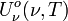 : J m-3 s ou bien J m-3 Hz-1,
: J m-3 s ou bien J m-3 Hz-1,- Selon la longueur d'onde :
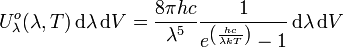
Unité SI de
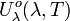 : J m-2 ou bien J m-3 μm-1.
: J m-2 ou bien J m-3 μm-1.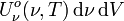 est l'énergie du rayonnement thermique dans le domaine de fréquence de ν à ν+dν qui se trouve dans le volume élémentaire dV de la cavité rayonnante.
est l'énergie du rayonnement thermique dans le domaine de fréquence de ν à ν+dν qui se trouve dans le volume élémentaire dV de la cavité rayonnante.Densité totale d'énergie du rayonnement d'une cavité à rayonnement isotrope
En intégrant la densité spectrale d'énergie du rayonnement d'une cavité rayonnante sur toutes les fréquences, on obtient la densité totale d'énergie du rayonnement de la cavité à rayonnement isotrope Uo :
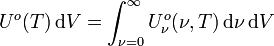
Le calcul de l'intégrale donne :
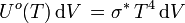
avec 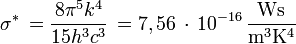 , Unité SI de Uo(T) : J m-3.
, Unité SI de Uo(T) : J m-3.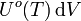 est l'énergie du rayonnement thermique de toutes les fréquences se trouvant dans le volume dV de la cavité.
est l'énergie du rayonnement thermique de toutes les fréquences se trouvant dans le volume dV de la cavité.Formulaire
Luminance énergétique spectrale : 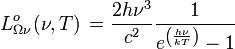
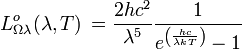
Unité : W m-2 Hz-1 sr-1 Unité : W m-2 μm-1 sr-1 Émittance énergétique spectrale : 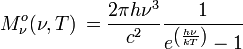
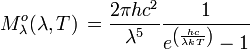
Unité : W m-2 Hz-1 Unité : W m-2 μm-1 Luminance énergétique : 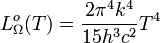
Unité : W m-2 sr-1 Émittance énergétique (loi de Stefan-Boltzmann): 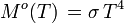 avec constante de Stefan-Boltzmann
avec constante de Stefan-Boltzmann 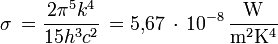
Unité : W m-2 Densité spectrale d'énergie d'une cavité à rayonnement isotrope : 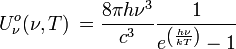
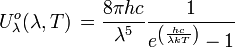
Unité : J m-3 Hz-1 Unité : J m-3 μm-1 Densité totale d'énergie d'une cavité à rayonnement isotrope : 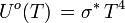 avec
avec 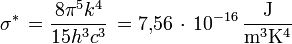
Unité : J m-3 On peut considérer le nombre de photons émis par unité de temps, plutôt que l'énergie rayonnée. Comme un photon de fréquence ν (ou de longueur d'onde
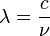 ) a une énergie hν (ou
) a une énergie hν (ou 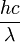 ) on a :
) on a :Luminance énergétique spectrale : 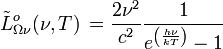
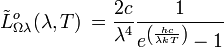
Unité : Photons s-1 m-2 Hz-1 sr-1 Unité : Photons s-1 m-2 μm-1 sr-1 Émittance energétique spectrale : 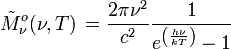
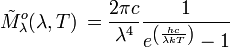
Unité : Photons s-1 m-2 Hz-1 Unité : Photons s-1 m-2 μm-1 Luminance énergétique : 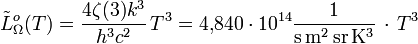
avec ζ(3) = 1,202056903... (constante d'Apéry où ζ désigne la fonction zêta de Riemann) Unité : Photons s-1 m-2 sr-1 Excitance énergétique (loi de Stefan-Boltzmann pour le taux de photons) : 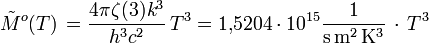
Unité : Photons s-1 m-2 Densité spectrale de photons d'une cavité à rayonnement isotrope : 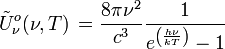
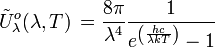
Unité : Photons m-3 Hz-1 Unité : Photons m-3 μm-1 Densité totale de photons d'une cavité à rayonnement isotrope : 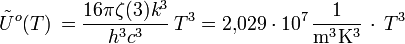
Unité : Photons m-3 Conséquences
La loi de Planck a unifié et confirmé des lois qui avaient été trouvées précédemment suites à des expériences ou des considérations thermodynamiques :
- la loi de Stefan-Boltzmann, qui donne l'énergie totale rayonnée par un corps noir, proportionnelle à T4,
- la loi du rayonnement de Rayleigh-Jeans, qui décrit la distribution spectrale d'énergie pour les grandes longueurs d'ondes,
- la loi du rayonnement de Wien, qui décrit la distribution spectrale d'énergie pour les petites longueurs d'ondes,
- la loi du déplacement, que Wien (1864-1928) formula en 1893, qui établit le rapport entre le maximum d'émission d'un corps noir et sa température.
Lois de rayonnement et hypothèse quantique
Considérons un exemple simplifié une cavité cubique de côté L et de volume V, renfermant le rayonnement électromagnétique de la cavité à rayonnement isotrope en équilibre thermique. A l'équilibre ne peuvent apparaître que des ondes stationnaires. Ces ondes peuvent être dirigées suivant n'importe quelle direction, mais doivent satisfaire à une même condition : un nombre entier de demies-longueurs d'onde doit passer entre deux surfaces parallèles de la cavité. Il ne peut donc y avoir que certains états vibratoires discrets. Le rayonnement total à l'intérieur de la cavité provient de ces différentes ondes stationnaires. Il y a
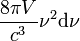 états vibratoires possibles dans l'intervalle de fréquences entre ν et ν+dν. (le nombre d'états vibratoires possibles augmente avec la fréquences). La densité d'états, c’est-à-dire le nombre d'états vibratoire possibles dans l'intervalle de fréquences entre ν et ν+dν et par unité de volume, vaut :
états vibratoires possibles dans l'intervalle de fréquences entre ν et ν+dν. (le nombre d'états vibratoires possibles augmente avec la fréquences). La densité d'états, c’est-à-dire le nombre d'états vibratoire possibles dans l'intervalle de fréquences entre ν et ν+dν et par unité de volume, vaut :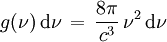 .
.En considérant ces états vibratoires comme des oscillateurs harmoniques de fréquence ν, on devrait s'attendre d'après le théorème d'équipartition de l'énergie à ce que, à l'équilibre thermique du milieu à la température T, chaque oscillateur porte l'énergie cinétique kT/2 et l'énergie potentielle kT/2, soit une énergie totale de kT. La densité d'énergie dans la cavité dans l'intervalle de fréquence entre ν et ν+dν serait alors :
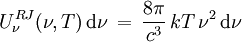 .
.Ceci est la loi de rayonnement de Rayleigh-Jeans. Elle rend bien compte de la densité d'énergie mesurée pour les faibles fréquences, mais prévoit faussement, avec l'augmentation de la fréquence, une augmentation quadratique de la densité d'énergie (catastrophe ultraviolette). Ce qui conduirait à ce que la cavité contienne une densité d'énergie infinie : chaque état vibratoire ne porte que l'énergie kT, mais une infinité de tels états vibratoires sont excités.
Les physiciens étaient conscients de cette conséquence et cherchèrent une formule différente pour résoudre le problème de la catastrophe ultraviolette. Wien établit sa loi du rayonnement en 1896, mais elle ne parvint pas à décrire les faibles fréquences. Planck l'améliora en 1900 en commençant par introduire un simple "-1" dans la loi du rayonnement de Wien. Cette formule n'était qu'empirique, mais elle correspondait bien aux mesures expérimentales sur l'ensemble du spectre de fréquences. Mais Planck n'en était pas satisfait. Il réussit à remplacer la constante C et c de la loi de Wien par des constantes naturelles; seul restait un facteur "h". C'était l'heure de naissance de la physique quantique : Planck devait concéder, contre ses propres convictions, que les transferts d'énergie ne se faisaient pas continûment mais de manière discrète, par des multiples d'unités de "h" (h comme Hilfskonstante : constante d'aide), appelé plus tard quantum d'action de Planck en son honneur.
D'après cette hypothèse quantique introduite par Planck, un oscillateur de fréquence ν ne peut prendre que des états d'énergie discrets multiples de hν, et ne peut être excité qu'à partir d'une énergie minimum hν. Les états vibratoires dont l'énergie minimale hν est nettement supérieure à l'énergie thermique kT disponible ne peuvent pas être excités et sont donc gelés. Les états vibratoires dont l'énergie minimale hν est très légèrement supérieure à kT peuvent être excités avec une certaine probabilité, et une fraction de ces états participent donc au rayonnement total de la cavité. Les états vibratoires d'énergie minimale hν inférieure à kT, donc de fréquences inférieures, sont très certainement excités.
La physique statistique montre que dans ces conditions, un état vibratoire porte en moyenne l'énergie
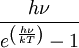 . En multipliant cette énergie par la densité d'états vibratoires possibles
. En multipliant cette énergie par la densité d'états vibratoires possibles 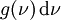 , on obtient la densité d'énergie de Planck :
, on obtient la densité d'énergie de Planck :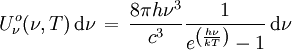 .
.
La catastrophe ultraviolette est donc évitée, car les états vibratoires de haute fréquence qui pourraient exister d'après des considérations géométriques ne peuvent pas être excités à cause de leur énergie d'excitation minimale hν trop importante, et ne participent donc pas à la densité d'énergie dans la cavité. La densité spectrale d'énergie diminue donc avec les plus hautes fréquence après être passée par un maximum, et la densité totale d'énergie reste finie.Répartition de l'intensité du rayonnement du corps noir
Émission
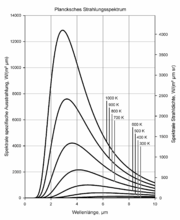
La première image ci-contre présente les spectres du rayonnement de Planck pour différentes températures entre 300 K et 1000 K. On reconnaît la forme typique de courbe en cloche avec un maximum clairement visible, une pente forte pour les faibles longueurs d'onde et une pente descendant plus doucement vers les grandes longueurs d'onde. Le maximum de rayonnement se décale vers les faibles longueurs d'onde avec la température croissante, comme le décrit la loi de déplacement de Wien. En outre comme le décrit la loi de Stefan-Boltzmann, l'exitance énergétique (correspondant à la surface sous la courbe de chaque exitance énergétique spectrale) augmente avec le puissance quatrième de la température. Une telle augmentation fait qu'il est difficile de présenter un tel graphe sur une plage de températures importante.
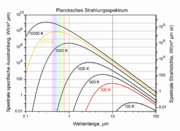
Pour pallier ce problème, le second graphe utilise une représentation logarithmique pour les deux axes. Sont présentés ici les spectres de rayonnement de Planck pour des températures de 100 K à 10 000 K.
La courbe rouge correspond à 300 K, ce qui correspond à la température ambiante. Le maximum pour cette courbe est atteint pour une longueur d'onde de 10 µm. C'est donc autour de cette longueur d'onde (infrarouges lointains) que se font les échanges d'énergie par rayonnement des objets à température ambiante. Les thermomètres infrarouges ou les caméras thermographiques fonctionnent dans ces longueurs d'ondes-ci.
La courbe pour 3000 K correspond au rayonnement typique d'une lampe à incandescence. Une partie du rayonnement est émis dans le domaine visible. Toutefois le maximum d'émission se situe encore dans l'infrarouge proche.
La courbe jaune correspond à 5777 K, la température effective du soleil. Le maximum d'émission est au milieu du domaine visible. Heureusement, la majorité du rayonnement thermique ultraviolet du soleil est absorbé par la couche d'ozone de l'atmosphère terrestre.
Réception
Comme on le voit sur le graphe précédent, l'exitance énergétique spectrale du soleil pour toutes les longueurs d'ondes est bien plus important que l'exitance des objets terrestres à 300 K. Pour une longueur d'onde de 10µm, un mètre carré de surface de soleil émet 400 fois plus qu'un mètre carré de façade de maison. Toutefois cela ne signifie pas que le rayonnement thermique environnant provient en majorité du soleil. Pour obtenir l'intensité de rayonnement rapportée à un mètre carré de surface réceptrice, Il faut multiplier la luminance spectrale par l'angle solide Ω visible depuis cette surface. Pour un observateur terrestre, le soleil ne représente qu'une très petite source (Ω = 6,8·10-5 sr). En comparaison avec un objet terrestre à 300 K remplissant le champ de vision de l'observateur à moitié (Ω = 3,14 sr), l'intensité de rayonnement du soleil à λ=10µm est plus faible d'un facteur 400·(6,8·10-5/3,14) ≈ 1/100, donc pratiquement négligeable. A ceci s'ajoute l'absorption d'une partie du rayonnement thermique du soleil par l'atmosphère, et une diminution supplémentaire due au fait que la surface réceptrice n'est pas ne reçoit pas le rayonnement orthogonalement.
Notes et références
- ↑ L'expression de la loi de Planck en fonction de la longueur d'onde correspond à l'usage courant qui en est fait en thermique industrielle, les échanges radiatifs s'effectuant généralement entre surfaces séparées par de l'air dont l'indice de réfraction est proche de 1 ; compte-tenu de la relation λν = c, cette loi peut également s'exprimer en fonction de la fréquence ν.
- ↑ Justification : quand un corps noir est soumis au rayonnement à l'intérieur d'une cavité à rayonnement isotrope de même température, il absorbe entièrement le rayonnement incident, mais doit remplacer le rayonnement absorbé par un rayonnement émis par lui-même pour conserver l'équilibre thermique. La luminance énergétique spectrale du rayonnement de la cavité doit être indépendante de la direction à l'équilibre, et comme le rayonnement émis par le corps noir a la même luminance, elle est également indépendante de la direction.
- ↑ La Commission internationale de l'éclairage recommande l'appellation exitance au lieu d'émittance énergétique.
- ↑ CODATA Value: Stefan-Boltzmann constant
Source
- (de) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en allemand intitulé « Plancksches Strahlungsgesetz ».
Articles connexes
- Portail de la physique
Catégories : Physique quantique | Physique statistique | Thermique | Loi en physique
Wikimedia Foundation. 2010.