- Équation de Darcy-Weisbach
-
L'équation de Darcy-Weisbach est une importante équation très utilisée en hydraulique[Paraschivoiu 1]. Elle permet de calculer la perte de charge due à la rugosité des conduites (« perte de charge linéaire », par opposition aux pertes de charge singulières).
Initialement l'équation est une variante de l'équation de Prony et a été développée par Henry Darcy avant d'être modifiée par Julius Weisbach (scientifique saxon) en 1845 qui lui donna sa forme actuelle:
avec
- hf - perte de charge due à la friction [m]
- f - coefficient de perte de charge [-]
- L - longueur de la conduite [m]
- Dh - diamètre hydraulique [m]
- v - vitesse du flux [m/s]
- g - constante d'accélération due à la gravité [m/s2]
Diagramme de Moody
Le coefficient de perte de charge, également appelé facteur ou coefficient de frottement, noté le plus souvent f (parfois λ), dépend du régime d’écoulement (laminaire ou turbulent) et des propriétés du fluide. En conditions isothermes, le nombre de Reynolds, qui est le rapport entre la puissance des forces de gravité et la dissipation visqueuse, suffit à caractériser le régime d'écoulement.
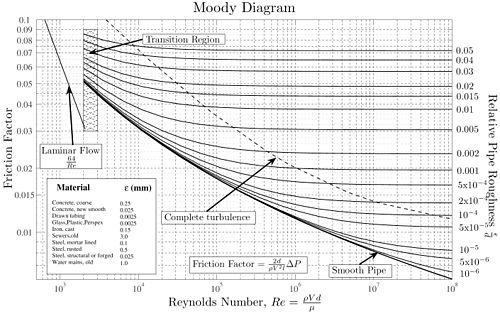
Plusieurs méthodes existent pour définir le coefficient de perte de charge. Une des plus connues est le diagramme de Moody qui est une abaque permettant de déterminer le coefficient de perte de charge à partir du nombre de Reynolds et de la rugosité du tuyau. Il est également possible de calculer directement ce paramètre à partir des 2 équations qui sont à la base du diagramme du Moody:
- pour un écoulement laminaire dans un tube circulaire, Re < 2000[1], on utilise la corrélation de Hagen-Poiseuille :
- pour un écoulement turbulent dans un tube circulaire, Re > 3000[1], on utilise la corrélation de Colebrook, également connu sous le nom d'équation de Colebrook-White :
- avec
la rugosité de la canalisation (quelques micromètres en général).
Rugosité pour quelques types de matériaux[Paraschivoiu 2] Matériau Rugosité [mm] fer forgé 0.12 - 0.3 conduite rivée 0.75 - 1-05 galvanisé 0.15 - 0.3 béton (petit tuyau) 0.15 - 0.25 béton rugueux 0.9 - 1.5 béton très rugueux 1.5 - 2.15 galerie rocheuse 90 - 300 - l'équation de Haaland[2] est une approximation de l'équation de Colebrook pour les tuyaux circulaires pleins:
- une autre approximation de l'équation de Colebrook pour les tuyaux circulaires pleins est donnée par l'équation de Swamee–Jain[3]:
- une autre approximation explicite plus complexe par rapport aux valeurs de l'équation de Colebrook est donnée par l'équation de Serghides[4]. La comparaison a été effectuée avec 70 points sur un large intervalle de valeurs tant pour le nombre de Reynmolds que pour la rugosité avec une erreur absolue maximale de 0.0031%.
- actuellement l'approximation la plus précise est donnée par l'équation de Goudar-Sonnad[5],[6] avec une erreur absolue maximale inférieure à 0.000364% pour plus de 10000 points compris entre 4000 < Re < 108 et 10-6 < ε/D < 10-2.
; 
; 
- s = bd + ln(d) ;
; 
Deux différentes possibilités sont disponibles pour calculer δ- 1)
- 2)
- pour des tuyaux industriels lisses en régime turbulent, la formule de Blasius[Paraschivoiu 3] peut être appliquée:
- pour des tuyaux industriels rugueux en régime turbulent, la formule de Blench[Paraschivoiu 4] permet une bonne approximation du coefficient de perte de charge:
Notes et références
- Ion Paraschivoiu, Michel Prud'homme et Patrick Vasseur, Mécanique des fluides, Montréal, Presses internationales Polytechnique, 2003, 450 p. (ISBN 2-553-01135-0), p. 324
- p. 317
- p. 321
- p. 317
- (en) Thomas Bradford Drew, Advances in chemical engineering, vol. 10, New York, Academic Press, Inc, 1978, 336 p. (ISBN 0-12-008510-0), p. 137
- (en) S.E. Haaland, « Simple and Explicit Formulas for the Friction Factor in Turbulent Flow », dans Journal of Fluids Engineering, vol. 105, no 1, mars 1983, p. 89-90 [lien DOI (page consultée le 17 décembre 2010)]
- (en) P.K. Swamee et A.K. Jain, « Explicit equations for pipe-flow problems », dans Journal of the Hydraulics Division, vol. 102, no 5, 1976, p. 657-664
- (en) T.K. Serghides, « Estimate friction factor accurately », dans Chemical Engineering, vol. 91, no 5, 1984, p. 63-64 (ISSN 0009-2460)
- (en) C.T. Goudar et J.R. Sonnad, « Comparison of the iterative approximations of the Colebrook-White equation », dans Hydrocarbon Processing, août 2008 [texte intégral]
- (en) C.T. Goudar et J.R. Sonnad, « Explicit Reformulation of the Colebrook−White Equation for Turbulent Flow Friction Factor Calculation », dans Industrial & Engineering Chemical Research, vol. 46, 2007, p. 2593-2600 [lien DOI (page consultée le 17 décembre 2010)]
Voir aussi
![f = \frac{0.25}{\left( \log_{10} \left[ \frac{\epsilon}{3.7 D} + \frac{5.74}{Re^{0.9}}\right] \right)^2}](f/99faeb8db92fb5fab0128a878d440c21.png)
![\frac{1}{\sqrt{f}} = a \left[ ln{\left( \frac{d}{q} \right)} + \delta \right]](3/e432b3975870c24ae9468826525859d6.png)
Wikimedia Foundation. 2010.
