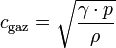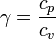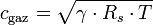Vitesse du bruit

Vitesse du bruit

Vitesse du son

La vitesse du son est la vitesse à laquelle se déplacent les ondes sonores. Elle varie suivant le milieu de propagation, et est définie de la manière suivante :

c = \frac{\omega}{k} (en m/s)

avec

Cela correspond à la définition de sa vitesse de phase. Dans le cas où le milieu est dispersif, elle est différente de la vitesse de groupe, qui est la vitesse de propagation de l'énergie sonore. Cette différence peut jouer un rôle lorsqu'on mesure la vitesse du son (voir plus bas). Il ne faut pas non plus confondre cette vitesse avec celle des molécules constituant le matériau, ni celle des particules fluides dans le cas d'un fluide.

Le principal facteur jouant sur la valeur de la vitesse du son est la densité du milieu de propagation : dans un gaz, sa vitesse est plus faible que dans un liquide. Par exemple, le son se propage approximativement à 340 m/s (1224 km/h) dans l'air à 15 °C, à 1 435 m/s (5166 km/h) dans l'eau douce et à environ 1 500 m/s (5400 km/h) dans l'eau de mer.

Cette propriété est notamment utilisée pour déterminer la qualité d'un béton, car une propagation plus rapide signifie que le béton contient peu de bulles d'air (la vitesse du son dans le béton est beaucoup plus élevée que dans l'air).

Sommaire

Histoire

Les premières expériences visant à mesurer la vitesse du son sont l'œuvre de Marin Mersenne et Pierre Gassendi durant la Renaissance. Cependant une valeur excessive sera donnée : 1 473 pieds par seconde.

Durant le XVIIe siècle d'autres expériences sont menées par Edmond Halley et Robert Boyle ainsi que par Giovanni Domenico Cassini et Christiaan Huygens, mais les résultats sont contradictoires. L'Académie des sciences française décide alors d'organiser des nouvelles expériences en 1738. À l'aide de coups de canon tirés la nuit (pour voir les flammes sortant de la bouche de l'arme) entre l'Observatoire de Paris, Montmartre, Fontenay-aux-Roses et Montlhéry, on estime la vitesse du son à 333 m/s dans une température de l'air à 0 °C. Une fois de plus, les résultats sont contradictoires avec la répétition de l'expérience en Allemagne.

En 1822, François Arago et Riche de Prony réalisent de nouvelles expériences plus rigoureuses, sur ordre du Bureau des longitudes. Cette fois-ci ils décident d'utiliser des tirs croisés, entre Villejuif et Montlhéry. Les coups de canons seront tirés en même temps, de cette manière, les expérimentateurs espèrent limiter les perturbations dues au taux d'hygrométrie, de vitesse du vent, de pression et de température, qu'ils pensent être la cause de l'échec de la précédente expérience. De plus, des chronomètres bien plus précis sont utilisés. Les expériences ont lieu dans les nuits du 21 et 22 juin 1822. Les résultats donnent la valeur de 340,88 m/s à une température de 15,9 °C. Après correction, la vitesse à 0 °C est de 330,9 m/s.

La vitesse du son est également déterminée dans d'autres environnements, comme en 1808 dans les solides par Jean-Baptiste Biot et en 1828 dans l'eau du Lac Léman par Jean-Daniel Colladon et Charles Sturm.

Vitesse du son dans un corps solide

Dans un solide, la vitesse des ondes mécaniques est dépendante de la masse volumique ρ et des constantes d'élasticité. Dans le cas des ondes de compression se propageant sans engendrer de déformation transverse (cas d'une tige infiniment fine) c'est le module de Young E qui entre en compte, et la vitesse se calcule ainsi :

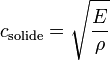c_{\mathrm{solide}} = \sqrt{\frac{E}{\rho}}.

Vitesse du son dans un fluide quelconque

Sans onde de cisaillement, la vitesse du son se propage seulement par compression. Si le son n'est pas trop fort (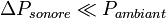\Delta P_{sonore} \ll P_{ambiant}), la compression et la détente du fluide peut être prise isentropique et la vitesse du son est :

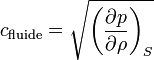c_{\mathrm{fluide}}=\sqrt{\left(\frac{\partial p}{\partial \rho}\right)_S} .

La racine carrée de la dérivée partielle de la pression par la densité à entropie constante.

Vitesse du son dans un liquide

La célérité du son dans un liquide est une fonction de la masse volumique ρ et du coefficient de compressibilité adiabatique χ et se calcule ainsi:

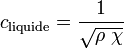c_{\mathrm{liquide}} = \frac{1}{\sqrt{\rho \; \chi}} .

Vitesse du son dans un gaz parfait

La vitesse du son dans un gaz parfait est fonction du coefficient isentropique γ (gamma), de la masse volumique ρ ainsi que de la pression p du gaz, et se calcule ainsi :

c_{\mathrm{gaz}} = \sqrt{\frac{\gamma \cdot p}{\rho}}

avec

\gamma = \frac{c_p}{c_v}

cp et cv étant les capacités thermiques massiques isobare et isochore.

La vitesse du son peut être aussi calculée à l'aide de l'équation d'état, du coefficient adiabatique γ (gamma), de la constante spécifique du gaz Rs et de la température T (K en kelvin).

c_{\mathrm{gaz}} = \sqrt{\gamma \cdot R_s \cdot T}

Avec pour l'air :

  • γ = 1,4
  • Rs = 287 J/kg/K

Le coefficient adiabatique γ dépend peu de la température T, la constante R est une grandeur indépendante de la température.

Cette vitesse est corrélée à la vitesse moyenne <v> des molécules. En effet, l'équation des gaz parfaits relie p à la température T et au volume V, et l'on a

pV γ = constante

Ce qui permet d'exprimer c en fonction de T seul, et donc de <v> Dans le cas d'un gaz parfait monoatomique (γ = 5/3), on a :

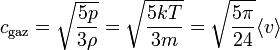
c_{\mathrm{gaz}} = \sqrt{\frac{5p}{3 \rho}} = \sqrt{\frac{5kT}{3m}} = \sqrt{\frac{5 \pi}{24}} \langle v \rangle
cgaz ≈ 0,81·<v'>

m étant la masse d'une molécule.

Cette relation indique que dans le domaine des gaz parfaits (c'est-à-dire des pressions modérées), la vitesse du son est proportionnelle à la vitesse des molécules, c'est-à-dire à la racine carrée de la température absolue.

Dans le cas de l'air (composé en majorité de gaz parfaits diatomiques), la célérité du son peut être approchée par la linéarisation suivante :

cair = (331,5 + 0,607·θ) m/s

où θ (thêta) est la température en degrés Celsius :

θ = T-273,15

T étant en K. Cette formule approchée permet d'obtenir de -20 °C à +40 °C une erreur inférieure à 0,2%.

Influence des autres facteurs

L'humidité de l'air influe peu.

Vitesse du son dans un gaz de Van der Waals

La vitesse du son dans un gaz de Van der Waals est fonction de deux variables thermodynamiques indépendantes, classiquement la température et la masse volumique, ainsi que de quatre paramètres, γ, Rs, a et b.

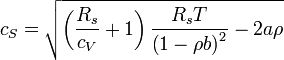
c_S = \sqrt{\left(\frac{R_s}{c_V}+1\right)\frac{R_sT}{\left(1-\rho b\right)^2}-2a\rho}

Fluides diphasique

Dans le cas d'un fluide diphasique (bulle d'air dans l'eau par exemple), la vitesse du son se trouve fortement modifiée. Le calcul de la vitesse du son est alors assez complexe et dépend notamment des relations qui unissent les deux fluides (par exemple, dans le cas d'un liquide avec des bulles de vapeur, il faudra prendre en compte les changements de phase). Néanmoins, un résultat général peut être tiré. La vitesse du son de ce mélange est bien inférieure à la plus petite des deux. Par exemple, pour un mélange eau/vapeur, la vitesse du son est autour de 30 m/s pour un taux de présence de 0,5.

Table des propriétés de l'air en fonction de la température

La table suivante présente l'évolution de quelques propriétés de l'air sous une pression d'une atmosphère en fonction de la température.

Influence de la température sur l'air
θ en °C c en m/s ρ en kg/m³ Z en N·s/m³
- 10 325,4 1,341 436,5
- 5 328,5 1,316 432,4
0 331,5 1,293 428,3
+ 5 334,5 1,269 424,5
+ 10 337,5 1,247 420,7
+ 15 340,5 1,225 417,0
+ 20 343,4 1,204 413,5
+ 25 346,3 1,184 410,0
+ 30 349,2 1,164 406,6

Méthodes expérimentales

Il existe plusieurs façons de mesurer la vitesse du son :

Par mesure d'un temps de propagation

En envoyant depuis un émetteur des impulsions sonores et en les détectant à l'aide d'un microphone, on peut mesurer le temps que met l'impulsion à parcourir la distance les séparant. Cela correspond donc à mesurer la vitesse de l'énergie sonore, c'est-à-dire la vitesse de groupe.

Par mesure de la fréquence et de la longueur d'onde

En mesurant successivement la fréquence et la longueur d'onde du son, on obtient sa vitesse en multipliant ces deux grandeurs. Cela correspond à la vitesse de phase. Il existe plusieurs méthodes permettant ces mesures :

  • Par exemple, un tube de Kundt est constitué d'un tube bouché à l'une des extrémités, et accolé à un haut-parleur à l'autre. Le son issu de ce haut-parleur est réfléchi par le côté du tube, et il s'installe une onde stationnaire dedans. En déplaçant un microphone dans le tube, on peut en détecter les ventres (maxima) et les nœuds (minima), ce qui permet de mesurer la longueur d'onde, puis la vitesse du son.
  • On peut aussi réaliser des ondes stationnaires dans les liquides, mais il est alors impossible d'utiliser un microphone pour les détecter. Cependant, ces ondes agissent sur la lumière de la même façon qu'un réseau optique. Il est donc possible, grâce à un montage optique, de mesurer la vitesse du son.

La différence principale entre ces deux méthodes est le résultat obtenu : d'une part la vitesse de phase, et d'autre part la vitesse de groupe. La différence entre ces deux grandeurs n'est cependant visible que lorsque la dispersion du milieu est importante, ce qui est rarement le cas.

Exemples de vitesses du son pour différents matériaux

Le tableau suivant donne quelques exemples pour quelques matériaux à une température de 20°C et sous une atmosphère.(En gardant la même source sonore )

Matériaux Célérité du son
(en m/s)
Air 343
Eau 1 480
Glace 3 200
Verre 5 300
Acier 5 200
Plomb 1 200
Titane 4 950
PVC (Mou) 80
PVC (Dur) 1 700
Béton 3 100
Hêtre 3 300
Granite 6 200
Péridotite 7 700
Sable sec 10 à 300

Il faut remarquer qu'il n'y a pas de vitesse du son dans le vide, puisqu'il n'y a aucune particule qui puisse servir de support aux ondes sonores.

Bibliographie

  • Michel Rival, Les grandes expériences scientifiques, dans le chapitre 1822 - Mesurer la vitesse du son, 1996 (ISBN 2-0202-2851-3)

Voir aussi

Articles connexes

Liens externes

  • Portail de la physique Portail de la physique
Ce document provient de « Vitesse du son ».

Wikimedia Foundation. 2010.

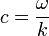Contenu soumis à la licence CC-BY-SA. Source : Article Vitesse du bruit de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • BRUIT DE FOND — En matière de transmission, on appelle bruit l’ensemble des signaux nuisibles qui se superposent au signal utile en un point quelconque d’une chaîne de mesure ou d’un système de transmission. Le signal utile représente l’information désirée alors …   Encyclopédie Universelle

  • BRUIT — Le bruit provoque, chez la plupart des gens, une sensation désagréable. Il s’agit d’un ennemi à combattre. Pourtant, sur le plan scientifique, il possède une définition très précise et représente un phénomène qui n’occasionne pas de gêne… …   Encyclopédie Universelle

  • Bruit Thermique — Le bruit thermique, également nommé bruit de résistance, ou bruit Johnson ou bruit de Johnson Nyquist est le bruit généré par l agitation thermique des porteurs de charges, c est à dire des électrons dans une résistance électrique en équilibre… …   Wikipédia en Français

  • vitesse — [ vitɛs ] n. f. • 1536; vistece « habileté » 1170; de vite 1 ♦ Le fait ou le pouvoir de parcourir un grand espace en peu de temps. ⇒ célérité, rapidité, vélocité. Se presser « pour gagner les autres de vitesse » (Renan). Lutter de vitesse avec… …   Encyclopédie Universelle

  • Bruit brownien — Mouvement brownien Mouvement brownien d une particule. Le mouvement brownien est une description mathématique du mouvement aléatoire d une « grosse » particule immergée dans un fluide et qui n est soumise à aucune autre interaction que… …   Wikipédia en Français

  • Bruit du tonnerre — Tonnerre Pour les articles homonymes, voir Tonnerre (homonymie) …   Wikipédia en Français

  • Bruit thermique — Le bruit thermique, également nommé bruit de résistance, ou bruit Johnson ou bruit de Johnson Nyquist est le bruit généré par l agitation thermique des porteurs de charges, c est à dire des électrons dans une résistance électrique en équilibre… …   Wikipédia en Français

  • Vitesse — Pour les articles homonymes, voir Vitesse (homonymie) …   Wikipédia en Français

  • Bruit radioélectrique — Compatibilité électromagnétique La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique ou électronique à fonctionner dans son environnement électromagnétique de façon satisfaisante et sans produire lui… …   Wikipédia en Français

  • Bruit électromagnétique — Compatibilité électromagnétique La compatibilité électromagnétique (CEM) est l aptitude d un appareil ou d un système électrique ou électronique à fonctionner dans son environnement électromagnétique de façon satisfaisante et sans produire lui… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”