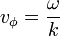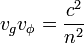- Vitesse de groupe
-
Vitesse d'une onde
 Schéma d'une onde se propageant
Schéma d'une onde se propageant
Une onde est une perturbation qui se déplace dans un milieu. Il est possible de lui associer deux vitesses d'onde.
Dans un milieu homogène, la propagation dans une direction donnée d'une onde monochromatique, ou sinusoïdale, se traduit par une simple translation de la sinusoïde à une vitesse appelée vitesse de phase ou célérité. Les ondes plus compliquées peuvent généralement être considérées comme des sommes de sinusoïdes de différentes fréquences ou pulsations (voir Analyse spectrale). Si la vitesse de phase ne dépend pas de la fréquence, l'onde résultante subit aussi une translation globale sans déformation. Dans le cas contraire, les composantes se dispersent. On peut alors souvent identifier des groupes d'ondes dont le maximum se déplace à une vitesse de groupe différente des célérités des composantes.
Sommaire
Vitesse de phase
La vitesse de phase d'une onde est la vitesse à laquelle la phase de l'onde se propage dans l'espace. Si l'on sélectionne n'importe quel point particulier de l'onde (par exemple la crête), il donnera l'impression de se déplacer dans l'espace à la vitesse de phase. La vitesse de phase s'exprime en fonction de la pulsation de l'onde ω et du vecteur d'onde k :
En effet, soit une onde monochromatique
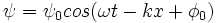 , plaçons nous sur une surface d'onde, i.e. l'ensemble des points ayant la même valeur de
, plaçons nous sur une surface d'onde, i.e. l'ensemble des points ayant la même valeur de 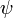 , par conséquent la même valeur de la phase
, par conséquent la même valeur de la phase 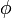 , c'est le plan de phase. Le plan de phase
, c'est le plan de phase. Le plan de phase 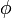 est en
est en  au temps
au temps 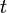 :
: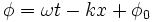
et en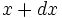 au temps
au temps 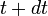 :
:
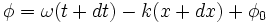
d'où par différence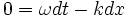
i.e.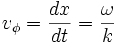
Cas des ondes électromagnétiques
Dans ce cas la vitesse de phase, égale à une constante c dans le vide, diminue dans un milieu transparent. Cette diminution est caractérisée par l'indice du milieu :
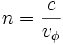
De plus, le milieu est dispersif : cet indice dépend du nombre d'onde (donc de la longueur d'onde), ce qui conduit à introduire la notion de vitesse de groupe.
La vitesse de phase d'une onde électromagnétique peut être supérieure à la vitesse de la lumière dans le vide dans certaines circonstances (en particulier lorsque l'indice de réfraction du matériaux est plus petit que 1 à certaines fréquences. Typiquement, on observe ce phénomène pour des rayons X) mais cela n'implique pas un transfert d'énergie ou d'information à une vitesse supérieure à celle de la lumière. En effet, une onde se déplace à sa vitesse de phase dans un groupe, qui lui se déplace à la vitesse de groupe de l'onde (voir ci-dessous).Les fronts d'onde se déplaçant à la vitesse de phase le font d'un front de la vitesse de groupe, au suivant. (voir l'animation dans la version anglaise de cette page.) Cependant, les fronts d'onde à la vitesse de phase ne peuvent pas exister en dehors de fronts d'onde qui voyagent à la vitesse de groupe. L'onde totale, c'est-à-dire le transfert d'information, s'effectue donc toujours à la vitesse la plus lente des deux. Or comme
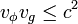 (voir plus bas) cette vitesse est inférieure à la vitesse de la lumière dans le vide. Une justification mathématique simple à cette affirmation est que l'onde totale est le produit d'une onde se déplaçant à vφ avec une onde se déplaçant à vg. Si l'un des deux est nul (par exemple si l'on se trouve dans une région ou que les fronts d'onde se déplaçant à vg n'ont pas eu le temps d'atteindre) le produit des deux, c'est à dire l'onde totale, doit aussi être nul. L'information se déplace donc toujours à la vitesse la plus lente des deux : vinformation = min(vg,vφ).
(voir plus bas) cette vitesse est inférieure à la vitesse de la lumière dans le vide. Une justification mathématique simple à cette affirmation est que l'onde totale est le produit d'une onde se déplaçant à vφ avec une onde se déplaçant à vg. Si l'un des deux est nul (par exemple si l'on se trouve dans une région ou que les fronts d'onde se déplaçant à vg n'ont pas eu le temps d'atteindre) le produit des deux, c'est à dire l'onde totale, doit aussi être nul. L'information se déplace donc toujours à la vitesse la plus lente des deux : vinformation = min(vg,vφ).On peut tenir un raisonnement similaire lorsque c'est la vitesse de groupe qui est la plus rapide, en particulier lorsque vg > c.
Vitesse de groupe
D'après ce qui précède, la vitesse de phase d'une onde monochromatique est égale au rapport de sa pulsation à son nombre d'onde. Considérons le cas le plus simple de deux ondes superposées de pulsations voisines et d'amplitude unité (les phases qui n'interviennent pas sont ignorées) :
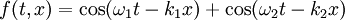
Selon la trigonométrie, une somme de cosinus se transforme en un produit de cosinus :
![f(t,x) = 2 \cos{1 \over 2}[(\omega_2 + \omega_1)t - (k_2 + k_1)x] \cos{1 \over 2}[(\omega_2 - \omega_1)t - (k_2 - k_1)x ]](/pictures/frwiki/99/ce99a8eb9dcf1865909320f29983cbd7.png)
Il apparaît un phénomène de battement dans lequel une sinusoïde de caractéristiques proches de celles des deux composantes, est modulée par une sinusoïde de plus basse fréquence dont la célérité est
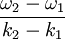 . Cette quantité représente la vitesse de groupe. Lorsque les deux fréquences de départ sont voisines, celle-ci est approximativement égale à
. Cette quantité représente la vitesse de groupe. Lorsque les deux fréquences de départ sont voisines, celle-ci est approximativement égale à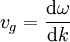
Dans le cas général de plus de deux ondes monochromatiques superposées, cette vitesse de groupe concerne une enveloppe plus compliquée qu'une sinusoïde.
La fonction qui exprime la pulsation en fonction du nombre d'onde définit la relation de dispersion. Lorsque la pulsation est directement proportionnelle au nombre d'onde, ce qui signifie que la vitesse de phase est indépendante de la pulsation, alors la vitesse de groupe est égale à cette vitesse de phase commune. Dans le cas contraire, l'enveloppe de l'onde se déforme au cours de la propagation.
Cas des ondes électromagnétiques
Dans le cas d'une onde électromagnétique, la vitesse de phase et la vitesse de groupe sont liées par la relation (qui fonctionne à basse fréquence uniquement) :
avec c vitesse de la lumière dans le vide.
La dispersion due à la vitesse de groupe est un effet important pris en compte pour la propagation d'informations par fibres optiques.
La vitesse de groupe est généralement présentée comme la vitesse à laquelle l'énergie ou l'information est transportée par une onde. Cette description est généralement valide, bien qu'il soit tout de même possible de réaliser des expériences dans lesquelles la vitesse d'impulsions laser envoyées dans des matériaux spécifiques soit supérieure à la vitesse de transmission du signal.
Voir aussi
Articles connexes
Liens externes
- Une animation sur Futura-Sciences
- Portail de la physique
Catégorie : Mécanique ondulatoire
Wikimedia Foundation. 2010.