Espace Localement Annelé

Espace Localement Annelé: Espace localement annelé

Un espace localement annelé est un espace topologique X muni d'un faisceau d'anneaux (commutatifs unitaires) O_X, appelé faisceau structural, tel qu'en tout point, l'anneau des germes de O_X soit un anneau local.

Si A est un anneau (commutatif unitaire), un espace localement annelé dont le faisceau structural est un faisceau de A-algèbres est un espace localement annelé sur A.

Soit $x$ un point de $X$ . Soit $m x$ l'idéal maximal de l'anneau local $O X, x$ . Le quotient $k (x): = O X, x / m x$ est le corps résiduel de $X$ en $x$ .

Exemples

les schémas;

les variétés différentielles, munies de leurs à valeurs dans ℂ;

les variétés complexes, munies de leurs fonctions holomorphes à valeurs dans ℂ;

les variétés algébriques.

Morphismes

Un morphisme entre deux espaces localement annelés (X, O_X) et (Y, O_Y) est la donnée d'une application continue f : X → Y et d'un morphisme de faisceaux d'anneaux f^# : O_Y → f_*O_X tel que pour tout x ∈ X, le morphisme d'anneaux O_{Y, f(x)} → O_{X, x} induit par f^# soit un morphisme d'anneaux locaux (c'est-à-dire qu'il envoie l'idéal maximal de l'anneau source dans l'idéal maximal de l'anneau but). Quand il n'y a pas d'ambiguïté possible, on note souvent le morphisme 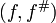$(f, f^{\#})$ par $f$ .

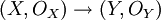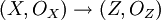Un exemple trivial de morphisme est l'identité d'un espace dans lui-même. On peut naturellement composer deux morphismes $(X, O_X) \to (Y, O_Y)$ , $(Y, O_Y) \to (Z, O_Z)$ pour obtenir un morphisme $(X, O_X) \to (Z, O_Z)$ . Un isomorphisme est un morphisme 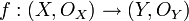$f : (X, O_X) \to (Y, O_Y)$ qui admet un morphisme inverse, c'est-à-dire dont la composition (à gauche ou à droite) avec $f$ est égale à l'identité.

Un morphisme (f, f^#) : (X, O_X) → (Y, O_Y) est une immersion si f est une immersion au sens topologique (c'est-à-dire que f induit un homéomorphisme de X sur son image), et si pour tout x ∈ X, le morphisme d'anneaux O_{Y, f(x)} → O_{X, x} est surjectif.

Exemple Soit $x$ un point de $X$ . Alors l'espace topologique ${x}$ muni du faisceau constant $k (x)$ est un espace localement annelé, et on a un morphisme 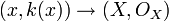$({x}, k(x)) \to (X, O_X)$ qui est l'inclusion canonique 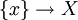$\{ x \} \to X$ au niveau du point $x$ . C'est une immersion.

Espaces tangent

Soit $x$ un point de $X$ . Soit $m x$ l'idéal maximal de l'anneau local $O X, x$ . Alors le quotient 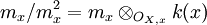$m_x/m_x^2=m_x\otimes_{O_{X,x}}k(x)$ est un espace vectoriel sur $k (x)$ . Son dual s'appelle l'espace tangent (de Zariski) de $X$ en $x$ . Dans les cas usuels (variétés différentielles, variétés analytiques complexes), cette notion coincide avec la définition standard.

Portail des mathématiques

Ce document provient de « Espace localement annel%C3%A9 ».

Catégorie : Géométrie algébrique

Contenu soumis à la licence CC-BY-SA. Source : Article Espace Localement Annelé de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Espace localement annele — Espace localement annelé Un espace localement annelé est un espace topologique X muni d un faisceau d anneaux (commutatifs unitaires) OX, appelé faisceau structural, tel qu en tout point, l anneau des germes de OX soit un anneau local. Si A est… … Wikipédia en Français
Espace localement annelé — Le concept d espace localement annelé est commun à différents domaines de géométrie, mais est plus utilisé en géométrie algébrique et en géométrie analytique complexe. Sommaire 1 Définition 1.1 Corps résiduel 2 Morphismes … Wikipédia en Français
GÉOMÉTRIE ALGÉBRIQUE — Sous sa forme actuelle, la géométrie algébrique est une branche de l’algèbre relativement récente (cf. ALGÈBRE, DEDEKIND). Pour «comprendre» les phénomènes d’intersection des courbes et des surfaces, il s’est révélé nécessaire d’élaborer des… … Encyclopédie Universelle
Géométrie algébrique — La géométrie algébrique est un domaine des mathématiques qui, historiquement, s est d abord intéressé à des objets géométriques (courbes, surfaces...) dont les coordonnées vérifiaient des équations ne faisant intervenir que des sommes et des… … Wikipédia en Français
Variete algebrique — Variété algébrique Pour les articles homonymes, voir variété. Une variété algébrique est, de manière informelle, l ensemble des racines communes d un ensemble de polynômes en plusieurs indéterminées. La géométrie algébrique est la théorie qui… … Wikipédia en Français
Variété algébrique — Pour les articles homonymes, voir variété. Une variété algébrique est, de manière informelle, l ensemble des racines communes d un nombre fini de polynômes en plusieurs indéterminées. C est l objet d étude de la géométrie algébrique. Les schémas… … Wikipédia en Français
Variété algébrique affine — Ne doit pas être confondu avec les variétés affines (ou sous espaces affines) en géométrie affine En géométrie algébrique, une variété affine est un modèle local pour les variétés algébriques, c est à dire que celles ci sont obtenues par… … Wikipédia en Français
Schéma (géométrie algébrique) — Pour les articles homonymes, voir Schéma. En géométrie algébrique, un schéma est un espace localement annelé (X,OX) localement isomorphe à un schéma affine. Le faisceau OX est appelé le faisceau structural. Un schéma affine est le spectre d un… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace Localement Annelé

Espace localement annelé

Exemples

Morphismes

Espaces tangent

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Espace Localement Annelé

Espace localement annelé

Exemples

Morphismes

Espaces tangent

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link