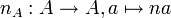Variete abelienne

En mathématiques, une variété abélienne A est, grosso modo, un groupe algébrique projectif. La projectivité (l'équivalent de compacité pour les variétés différentielles ou analytiques) donne une certaine rigidité à la strucutre. En géométrie arithmétique, c'est un objet central.

Sommaire 1 Définition 2 Propriétés basiques 3 Isogénie 4 Anneaux d'endomorphismes 5 Module de Tate 6 Référence

Définition

Une variété abélienne sur un corps k est un groupe algébrique A sur k, dont la variété algébrique sous-jacente est projective, connexe et géométriquement réduite. Cette dernière condition veut dire que lorsque l'on étend le corps de base k à une clôture algébrique de k, la nouvelle variété est réduite (cela implique que A est réduite). Si k est de caractéristique nulle, la condition "géométriquement réduite" est automatiquement satisfaite pour tout groupe algébrique sur k (Théorème de Cartier).

Exemple: Les variétés abéliennes de dimension 1 sont les courbes elliptiques.

La jacobienne d'une courbe algébrique projective non-singulière géométriquement connexe, de genre g, est une variété abélienne de dimension g.

Si A est une variété abélienne de dimension g sur ℂ, alors A(ℂ) est naturellement une variété analytique complexe, et même un groupe de Lie. C'est le quotient (au sens de la géométrie analytique complexe) de ℂ^g par un réseau, le quotient admettant un plongement dans un espace projectif.

Propriétés basiques

Une variété abélienne A est toujours non-singulière, et la loi de groupe sur A est commutative.

Si A et B sont des variétés abéliennes sur k, et si 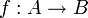est un morphisme de variétés algébriques qui envoie le zéro de A sur le zéro de B, alors f est un hommorphisme de groupes algébriques (c'est-à-dire que f est compatible avec les structures de groupes algébriques sur A et B).

Structure de la torsion Si A est une variété abélienne de dimension g définie sur un corps k et si n est un entier naturel premier à la caractéristique de k, alors l'ensemble des éléments de A à coordonnées dans une clôture algébrique 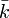de k et qui sont d'ordre divisant n (c'est donc le noyau de l'application multiplication par n dans dans le groupe 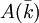) est un groupe fini, isomorphe à 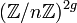. En particulier, les points de A à coordonnées dans k et qui sont d'ordre divisant n est un sous-groupe de .

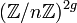Si k est de caractéristique p > 0, alors il existe un entier r compris entre 0 et g tel que pour toute puissance n de p, soit isomorphe à 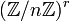. On appelle r le p-rang de A. On dit que A est ordinaire si son p-rang prend la valeur maximale, c'est-à-dire g.

Isogénie

Un homomorphisme 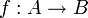de variétés abéliennes est une isogénie si A et B ont la même dimension et si le noyau de f est fini. Un exemple typique d'isogénie est la multiplication par n :

pour tout entier naturel n (même quand il est divisible par la caractéristique de k).

Théorème Si 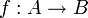est une isogénie, alors il existe une isogénie telle que fg = n_B et gf = n_A.

Définition On dit que A est simple si elle n'a pas d'autres sous-variété abélienne que {0} et elle-même. Par exemple toute courbe elliptique est simple, mais pas le produit de deux courbes elliptiques.

Théorème (irréductibilité complète de Poincaré) Si 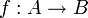est un homomorphisme de variété abéliennes surjectif, alors il existe une sous-variété abélienne C de A telle que A soit isogène à .

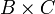On en déduit que toute variété abelienne A est isogène à un produit de variétés abeliennes simples. L'ensemble de ces facteurs simples est unique à permutations et isogénies près.

Anneaux d'endomorphismes

Soit A une variété abélienne sur k de dimension g. On note End(A) l'ensemble des endomorphismes de A.

Théorème L'ensemble End(A) est naturellement un anneau. Comme module sur ℤ, il est libre de rang au plus 4g.

La structure de l'anneau End(A) est plus simple lorsqu'on permet d'inverser les entiers naturels. On note End^0(A) le produit tensoriel sur ℤ de End(A) par le corps des rationnels Q.

Théorème Si A est isogène au produit 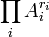avec A_i simples, 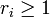, et A_i non isogène à A_j si i est différent de j, alors End⁰(A) est isomorphe au produit 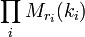, où k_i = End⁰(A_i) est un corps gauche de dimension finie sur k, et où M_n désigne l'algèbre des matrices carré d'ordre n.

Module de Tate

Nous avons vu que sur ℂ, A est un quotient (comme variété analytique) de ℂⁿ par un réseau Λ. Sur un corps k quelconque, il existe un équivalent du réseau Λ, c'est le module de Tate.

Définition Soit l un nombre premier distinct de l'exposant caractéristique de k. On a un système projectif , où les applications de transition sont la multiplication par l. Alors le module de Tate (du nom du mathématicien John Tate) de A est la limite projective, notée T_l(A), de .

Le module de Tate est naturellement un module sur l'anneau ℤ_l des entiers l-adiques.

Proposition T_l(A) est isomorphe à ℤ.

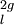Référence

• Marc Hindry and Joseph H. Silverman: Diophantine Geometry: An Introduction, Graduate Texts in Mathematics, Springer, 2000

• James Milne: Abelian varieties, in Arithmetical Geometry (edited by Cornell and Silverman), Springer, 1984

• James Milne : Abelian varieties, http://www.jmilne.org/math/CourseNotes/math731.html

• David Mumford: Abelian varieties, 1974 (ré-édité en 1985)

• André Weil: Courbes algébriques et variétés abéliennes, 1948

• Portail des mathématiques