Corps topologique

Corps topologique

Anneau topologique

En mathématiques, un anneau topologique est un anneau muni d'une topologie compatible avec les opérations internes, c'est-à-dire telle que l'addition, l'application opposée[1] et la multiplication soient continues.

Un corps topologique est un corps muni d'une topologie qui rend continues l'addition, la multiplication et l'application inverse[2].

Ces structures étendent la notion de groupe topologique.

Sommaire

Exemples

  • Tous les corps de nombres usuels (rationnels, réels, complexes, p-adiques) ont une ou plusieurs topologies classiques qui en font des corps topologiques. Il s'agit essentiellement des topologies induites par la distance usuelle ou la distance p-adique.
  • L'ensemble des applications d'un ensemble X vers un anneau topologique constitue un anneau topologique pour la topologie de la convergence simple. Lorsque l'ensemble X est lui-même un espace topologique, le sous-anneau des fonctions continues est un anneau topologique pour la topologie compact-ouvert
  • Tout sous-anneau d'un anneau topologique est un anneau topologique pour la topologie induite.
  • Tout anneau muni de la topologie discrète ou de la topologie grossière constitue un anneau topologique.

Topologie I-adique

Étant donné un anneau commutatif R et un idéal I de R, la topologie I-adique de R est définie par la base de voisinages en chaque point x de R de la forme : x + In, où n décrit tous les entiers naturels.

Cette topologie fait de l'anneau R un anneau topologique, qui est séparé si et seulement si l'intersection des puissances de l'idéal I est réduit à l'élément nul :

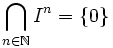\bigcap_{n \in \mathbb{N}}I^n = \{0\}.

Dans ce cas, la topologie est métrisable par une distance ultramétrique définie de la manière suivante :

pour tous x≠y éléments de R,
d(x,y) = 1 / 2k
où k est la plus grande puissance de l'idéal qui contient la différence x − y.

La topologie p-adique sur les entiers relatifs est ainsi construite avec l'idéal I des multiples entiers de p.

Complétion d'un anneau métrisable

Lorsqu'un anneau topologique est métrisable, c'est-à-dire si sa topologie peut être associée à une distance, l'ensemble de ses suites de Cauchy forme lui aussi un anneau. Le quotient de cet anneau de suites par l'idéal des suites convergeant vers 0 constitue le complété de l'anneau de départ.

Notes

  1. ↑ La continuité de l'application opposée est automatiquement vérifiée si l'anneau est unitaire.
  2. ↑ Il existe toutefois des corps muni d'une topologie qui en font des anneaux topologiques sans satisfaire cette dernière condition.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Anneau topologique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Corps topologique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • TOPOLOGIQUE (ALGÈBRE) — L’algèbre topologique est consacrée à l’étude d’ensembles munis d’une topologie et d’une structure algébrique définie par des lois de composition continues (cf. TOPOLOGIE, ALGÈBRE). Les exemples les plus importants sont les groupes topologiques,… …   Encyclopédie Universelle

  • CORPS (mathématiques) — La structure de corps n’est en fait qu’un cas particulier de la structure plus générale d’anneau [cf. ANNEAUX ET ALGÈBRES]; en plus des axiomes généraux, on stipule que le groupe multiplicatif des éléments inversibles est le complémentaire de 0.… …   Encyclopédie Universelle

  • CORPS - Le corps et la psychanalyse — Le corps est, en psychanalyse, une réalité difficile à penser, car elle défie les approches physiologiques et philosophiques, et décisive pourtant, puisque la sexualité humaine – considérée dans la jouissance ou dans des activités sublimatoires – …   Encyclopédie Universelle

  • Corps des réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… …   Wikipédia en Français

  • Anneau Topologique — En mathématiques, un anneau topologique est un anneau muni d une topologie compatible avec les opérations internes, c est à dire telle que l addition, l application opposée[1] et la multiplication soient continues. Un corps topologique est un… …   Wikipédia en Français

  • Anneau topologique — En mathématiques, un anneau topologique est un anneau muni d une topologie compatible avec les opérations internes, c est à dire telle que l addition, l application opposée[1] et la multiplication soient continues. Un corps topologique est un… …   Wikipédia en Français

  • Espace Vectoriel Topologique — Les espaces vectoriels topologiques sont une des structures de base de l analyse fonctionnelle. Ce sont des espaces munis d une structure topologique associée à une structure d espace vectoriel. Des exemples connus d espaces vectoriels… …   Wikipédia en Français

  • Espace vectoriel topologique — Les espaces vectoriels topologiques sont une des structures de base de l analyse fonctionnelle. Ce sont des espaces munis d une structure topologique associée à une structure d espace vectoriel, avec des relations de compatibilité entre les deux… …   Wikipédia en Français

  • Partie bornée d'un espace vectoriel topologique — Pour les articles homonymes, voir Partie bornée. En analyse fonctionnelle et dans des domaines mathématiques reliés, une partie d un espace vectoriel topologique est dite bornée si tout voisinage du vecteur nul peut être dilaté de manière à… …   Wikipédia en Français

  • Espace topologique — La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un cadre général pour traiter des notions de limite, de continuité, et de voisinage. Les espaces topologiques forment le socle conceptuel permettant de définir… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”