Troisième loi de Kepler

En astronomie, les lois de Kepler décrivent les propriétés principales du mouvement des planètes autour du Soleil, sans les expliquer. Elles ont été découvertes par Johannes Kepler à partir des observations et mesures de la position des planètes faites par Tycho Brahe, mesures qui étaient très précises pour l'époque.

Copernic avait soutenu en 1543 que les planètes tournaient autour du Soleil, mais il les laissait sur les trajectoires circulaires du vieux système de Ptolémée hérité de l'antiquité grecque.

Les deux premières lois de Kepler furent publiées en 1609 et la troisième en 1618. Les orbites elliptiques, telles qu'énoncées dans ses deux premières lois, permettent d'expliquer la complexité du mouvement apparent des planètes dans le ciel sans recourir aux épicycliques du modèle ptoléméen.

Peu après, Isaac Newton découvrit en 1687 la loi de l'attraction gravitationnelle (ou gravitation), induisant celle-ci, par le calcul, des trois lois de Kepler.

Sommaire 1 Énoncé des trois lois de Kepler 1.1 Première loi – Loi des orbites 1.2 Seconde loi – Loi des aires 1.3 Troisième loi – Loi des périodes 2 Forme newtonienne de la troisième loi de Kepler 3 Découverte de nouveaux corps célestes 4 Voir aussi 4.1 Articles connexes 4.2 Liens externes

Énoncé des trois lois de Kepler

Première loi – Loi des orbites

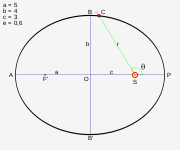
Les planètes du système solaire décrivent des trajectoires elliptiques dont le Soleil occupe l'un des foyers.

Dans le référentiel héliocentrique, le Soleil occupe toujours l'un des deux foyers de la trajectoire elliptique des planètes qui gravitent autour de lui. À strictement parler, c'est le centre de masse qui occupe ce foyer ; la plus grande différence est atteinte avec Jupiter qui, du fait de sa masse importante, décale ce centre de masse de 743 075 km ; soit 1,07 rayons solaires — des déplacements plus importants peuvent être obtenus en cumulant les effets des planètes sur leur orbite. À l'exception de Mercure, les ellipses que décrivent les centres de gravité des planètes ont une très faible excentricité orbitale, et leur trajectoire est quasi-circulaire.

De cette première loi, on déduit que le Soleil exerce sur une planète une force centripète.

Seconde loi – Loi des aires

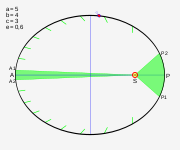
Si S est le Soleil et M une position quelconque d'une planète, l'aire balayée par le segment [SM] entre deux positions C et D est égale à l'aire balayée par ce segment entre deux positions E et F si la durée qui sépare les positions C et D est égale à la durée qui sépare les positions E et F. La vitesse d'une planète devient donc plus grande lorsque la planète se rapproche du Soleil. Elle est maximale au voisinage du rayon le plus court (périhélie), et minimale au voisinage du rayon le plus grand (aphélie).

De cette deuxième loi, on déduit que la force exercée sur la planète est constamment dirigée vers le Soleil. Kepler écrira à un collègue : Une chose est certaine : du Soleil émane une force qui saisit la planète.

Troisième loi – Loi des périodes

Le carré de la période sidérale T d'un objet (temps entre deux passages successifs devant une étoile lointaine) est directement proportionnel au cube du demi-grand axe a de la trajectoire elliptique de l'objet :

,

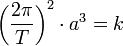avec k constant. Les lois de la gravitation universelle énoncées par Isaac Newton permettent de déterminer cette constante en fonction de la constante de gravitation G et la masse du Soleil M_⊙ selon

.

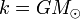De cette troisième loi (appelée aussi « loi harmonique de Kepler ») car elle exprime un invariant à travers tout le système solaire, « donc » une certaine harmonie de celui-ci (le mouvement de toutes les planètes est unifié en une loi universelle) on déduit qu'il existe un facteur constant entre la force exercée et la masse de la planète considérée, qui est la constante de gravitation universelle, ou constante gravitationnelle.

Cette formule avec celles de l'ellipse permet de calculer les différents paramètres d'une trajectoire elliptique à partir de très peu d'informations. En effet, Johann Lambert (1728 - 1777) montra que la connaissance de trois positions datées permettaient de retrouver les paramètres du mouvement (pour une discussion plus approfondie, voir Lois de Kepler, démonstration ; puis satellite, orbitographie).

Forme newtonienne de la troisième loi de Kepler

Newton comprit le lien entre les lois de la mécanique classique et la troisième loi de Kepler. Il en déduisit la formule suivante :

,

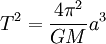où

• T est la période de l'objet,
• a est le demi grand axe de la trajectoire elliptique,
• G est la constante de la gravitation universelle,
• M est la masse de l'objet au centre (en l'occurrence le Soleil si l'on applique la loi aux planètes)

Les lois de Kepler ne sont pas seulement applicables aux planètes mais à chaque fois qu'une masse se trouve en orbite autour d'une autre masse. C'est le cas, par exemple, de la Lune et de la Terre ou d'un satellite artificiel en orbite autour de celle-ci.

Découverte de nouveaux corps célestes

Johannes Kepler découvrit ses lois grâce à un travail d'analyse considérable des tables astronomiques établies par Tycho Brahe. En particulier l'étude de Mars lui permit de montrer que le mouvement n'était pas épicyclique mais elliptique.

Ses lois ont permis, elles-mêmes, d'affiner les recherches astronomiques et de mettre en évidence des irrégularités de mouvements de corps connus, par une étonnante progression de l'analyse.

L'exemple le plus spectaculaire fut celui des irrégularités d'Uranus qui permit la « découverte » de Neptune par Le Verrier (1811 - 1877), par le calcul : découverte confirmée par l'observation de Galle (1812 - 1910) en 1846.

Voir aussi

Articles connexes

• Cinématique > Mouvement elliptique
• Équation du temps. Donne la différence entre l'heure indiquée par le Soleil et celle indiquée par une montre.
• Lois de Kepler, démonstration
• Mouvement keplerien
• Problème à deux corps
• Révolution copernicienne

Liens externes

• (fr) Activités pédagogiques Kepler
• (fr) Définition et démonstration des lois de Kepler, sur le site Astrophy
• (fr) Démonstration des trois lois de Kepler et de propriétés d'une ellipse

• Portail de l’astronomie