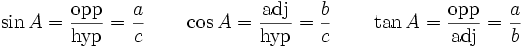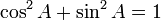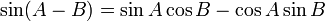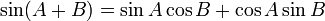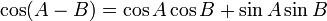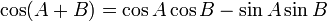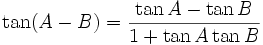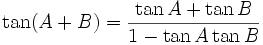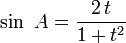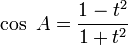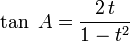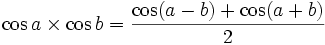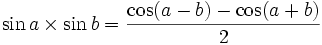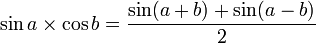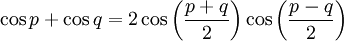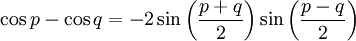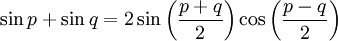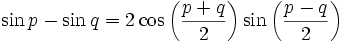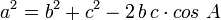Trigométrie dans un triangle

Trigonométrie

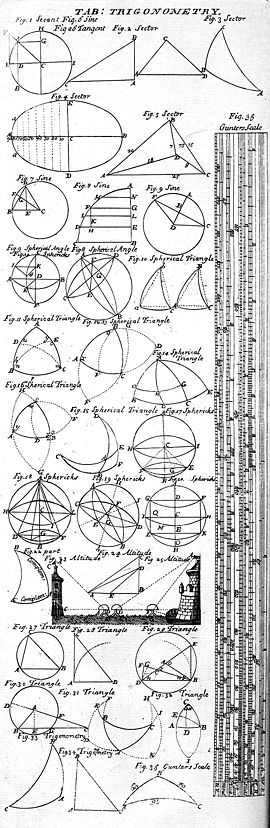
Planche sur la Trigonométrie, 1728 Cyclopaedia

La trigonométrie (du grec ancien τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.

Sommaire

1 Présentation
- 1.1 Histoire de la trigonométrie
- 1.2 Applications
2 Trigonométrie
3 Formules de trigonométrie
4 Quelques problèmes célèbres
5 Voir aussi

Présentation

Histoire de la trigonométrie

Premières techniques de mesure du triangle

Les origines de la trigonométrie remontent aux civilisations d'Égypte antique, de Mésopotamie et de la vallée de l'Indus, il y a plus de 4000 ans. Il semblerait que les Babyloniens aient basé la trigonométrie sur un système numérique à base 60. Lagadha (-1350 ; -1200) est le premier mathématicien à utiliser la géométrie et la trigonométrie pour l'astronomie. La plupart de ses travaux sont aujourd'hui détruits.

La première utilisation de sinus apparaît dans les sulba Sutras en Inde, entre 800 et 500 avant J.C., où le sinus de π/4 (45°) est correctement calculé comme 1/√2 dans un problème de construction d'un cercle de même aire qu'un carré donné (le contraire de la quadrature du cercle).

Les astronomes grecs

L'astronome et mathématicien grec Hipparque de Nicée (-190 ; -120) construisit les premières tables trigonométriques sous la forme de tables de cordes : elles faisaient correspondre à chaque valeur de l'angle au centre (avec un division du cercle en 360°), la longueur de la corde interceptée dans le cercle, pour un rayon fixe donné. Ce calcul correspond au double du sinus de l'angle moitié, et donne donc, d'une certaine façon, ce que nous appelons aujourd'hui une table de sinus. Toutefois, les tables d'Hipparque n'étant pas parvenues jusqu'à nous, elles ne nous sont connues que par le grec Ptolémée, qui les publia, vers l'an 150, avec leur mode de construction dans son Almageste. C'est ainsi qu'elles furent redécouvertes à la fin du Moyen-Âge par Georg von Purbach et son élève Regiomontanus. On attribue à Ménélaüs d'Alexandrie (fin du Ier siècle) des développements en trigonométrie sphérique, au moins partiellement présents dans l'Almageste et longtemps attribués à Ptolémée lui-même.

Le mathématicien indien Aryabhata, en 499, donne une table des sinus et des cosinus. Il utilise zya pour sinus, kotizya pour cosinus et otkram zya pour l'inverse du sinus. Il introduit aussi le sinus verse.

Un autre mathématicien indien, Brahmagupta, utilise en 628 l'interpolation numérique pour calculer la valeur des sinus jusqu'au second ordre.

Essor dans le monde musulman

Omar Khayyam (1048-1131) combine l'utilisation de la trigonométrie et la théorie de l'approximation pour fournir des méthodes de résolutions d'équations algébriques par la géométrie. Des méthodes détaillées de constructions de tables de sinus et cosinus pour tous les angles sont écrites par le mathématicien Bhaskara en 1150. Il développe aussi la trigonométrie sphérique. Au XIII^e siècle, Nasir al-Din Tusi, à la suite de Bhaskara, est probablement un des premiers à considérer la trigonométrie comme une discipline distincte des mathématiques. Enfin, au XIV^e siècle, Al-Kashi réalise des tables de fonctions trigonométriques lors de ses études en astronomie.

En Europe : redécouverte de Ptolémée

En Europe, la trigonométrie se développe vers le milieu du XIV^e siècle avec la traduction en latin des œuvres de Ptolémée. Les pionniers en ce domaine sont Georg von Purbach et surtout son étudiant Regiomontanus. Suivent au début du XVI^e siècle les traités d'Oronce Finé, Pedro Nunes et Joachim Rheticus. Le mathématicien silésien Bartholomäus Pitiscus publie un travail remarquable sur la trigonométrie en 1595, dont le titre (Trigonometria) a donné son nom à la discipline. 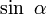C'est le mathématicien flamand Adrien Romain qui introduit la notation moderne $\sin \ \alpha$ .

Applications

Article détaillé : Applications de la trigonométrie.

Les applications de la trigonométrie sont immenses. En particulier, elle est utilisée en astronomie avec la technique de triangulation qui permet de mesurer la distance entre les étoiles. Les autres champs où la trigonométrie intervient (liste non exhaustive) : acoustique, optique, électronique, statistiques, économie, biologie, chimie, médecine, physique, météorologie, géodésie, géographie, cartographie, cryptographie, etc.

Trigonométrie

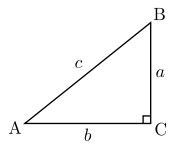
Une définition possible des fonctions trigonométriques est d'utiliser les triangles rectangles, c’est-à-dire les triangles qui possèdent un angle droit (90° (degrés) ou π/2 radians).

Et parce que la somme des angles d'un triangle fait 180° (ou π radians), l'angle le plus grand dans un tel triangle est l'angle droit. Le côté le plus long dans un triangle rectangle, c’est-à-dire le côté opposé à l'angle le plus grand (l'angle droit), s'appelle l'hypoténuse.

Dans la figure à droite, l'angle $\widehat{ACB}$ forme l'angle droit. Le côté AB l'hypoténuse.

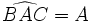Les fonctions trigonométriques se définissent ainsi, avec l'angle $\widehat{BAC} = A$ :

$\sin A = {\mbox{opp} \over \mbox{hyp}} = {a \over c} \qquad \cos A = {\mbox{adj} \over \mbox{hyp}} = {b \over c} \qquad \tan A = {\mbox{opp} \over \mbox{adj}} = {a \over b}$

Avec opp pour côté opposé, adj pour côté adjacent et hyp pour hypoténuse.

Ce sont les fonctions trigonométriques les plus importantes et il en existe beaucoup d'autres. Elles ont été définies pour les angles entre 0° et 90° (soit entre 0 et π/2 radians). En utilisant le cercle unité, on peut étendre cette définition.

Formules de trigonométrie

Pour retrouver toutes les autres formules de trigonométrie, voir l'article : Identité trigonométrique.

Identité fondamentale

Quel que soit l'angle A, on a:

$\cos^{2} A + \sin^{2} A = 1 \,$

Formules d'addition et de différence

$\sin (A - B) = \sin A \cos B - \cos A \sin B \,$

$\sin (A + B) = \sin A \cos B + \cos A \sin B \,$

$\cos (A - B) = \cos A \cos B + \sin A \sin B \,$

$\cos (A + B) = \cos A \cos B - \sin A \sin B \,$

$\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,$

$\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,$

Formules de l'arc moitié

Ces formules sont importantes à retenir car elles interviennent dans de très nombreux problèmes. En posant : 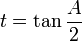$t = \tan \frac{A}{2}$ , on a alors :

$\sin\ A = {{2\,t} \over {1+t^{2}}}$

$\cos\ A = {{1-t^{2}} \over {1+t^{2}}}$

$\tan\ A = {{2\,t}\over {1-t^{2}}}$

Formules de développement et de factorisation (Formules de Simpson)

Développement

$\cos a \times \cos b = {{\cos(a-b)+\cos(a+b)} \over 2}$

$\sin a \times \sin b = {{\cos(a-b)-\cos(a+b)} \over 2}$

$\sin a \times \cos b = {{\sin(a+b) + \sin(a-b)} \over 2}$

Factorisation

$\cos p + \cos q = 2 \cos \left( {{p+q} \over 2} \right) \cos \left( {{p-q} \over 2} \right)$

$\cos p - \cos q = -2 \sin \left( {{p+q} \over 2} \right) \sin \left( {{p-q} \over 2} \right)$

$\sin p + \sin q = 2 \sin \left( {{p+q} \over 2} \right) \cos \left( {{p-q} \over 2} \right)$

$\sin p - \sin q = 2 \cos \left( {{p+q} \over 2} \right) \sin \left( {{p-q} \over 2} \right)$

Théorème d'Al-Kashi ou Loi des cosinus

$a^2 = b^2 + c^2 - 2\,b\,c \cdot cos\ A$

Cette formule a une importance particulière en triangulation et a servi à l'origine en astronomie (voir Théorème d'Al-Kashi pour plus de détails). On doit au mathématicien Ghiyath al-Kashi, de l'école de Samarcande, de mettre le théorème sous une forme utilisable pour la triangulation au cours du XV^e siècle.

Résoudre un triangle

C'est, étant donné un côté et deux angles adjacents, ou un angle et deux côtés adjacents, ou à la rigueur deux côtés b et c et l'angle B, trouver le triangle correspondant, c'est-à-dire, a, b, c, A, B, C (et vérifier une des règles non appliquée dans le processus). On résout ce genre de problème à l'aide des formules précédentes (plus la formule de projection évidente a = b.cosC +c.cosB).

Exemple : Sur l'axe Ox, OB = 1 et OC = 1.5 . OBM = 60° et OCM = 30° Trouver M :

On résout ainsi : faire l'épure ; M se trouve en (x= 0.75 ; y = 0.45) environ . Raisonner : triangle BMC : B = 120°, C = 30° donc M = 30° ; donc triangle isocèle en B : BM = 0.5 ; puis CM = 2.(0.5).cos C = sqrt(3)/2. Soit H la projection de M sur l'axe : HM = y et angle HMB = 30°. Il en résulte que y = sqrt(3)/4 = 0,433 et x = 1-(0,5)/2 = 0,75 . La distance OM = sqrt(3)/2 = MC, et azimut de M = 30°, angle OMB = 90°.

Il est rare du point de vue cadastral que les cas soient aussi simples.

En général on demande 4 à 6 ChS (chiffres significatifs) : les calculettes ont considérablement réduit le travail assez fastidieux de "réduction des triangles". Rappelons que la mesure du degré du méridien terrestre de Paris s'est effectué de la sorte entre Malvoisine et Montlhéry par l'abbé Picard, dans le milieu du XVII^e siècle.

La surface S du triangle se calcule par la formule des sinus ou la formule d'Héron (d'Alexandrie) qui s'en déduit : $S 2 = p (p - a)(p - b)(p - c).$

Article détaillé : Résolution d'un triangle

Quelques problèmes célèbres

La quadrature du cercle : construire un carré de même aire qu'un cercle donné à l'aide d'une règle et d'un compas, ce problème est insoluble.

L'approximation sin A = A - k A³ avec k = 1/6 quand A est petit (en radians !) peut se déduire de la formule sin(3A) = 3.sinA -4 sin³A : les termes en A³ donnent : -k27 = -3k -4 , CQFD.

La flèche d'une corde AB sous tendant l'arc AOB = 2 α : soit I milieu de AB et CD le diamètre passant par I : ID = flèche telle que f( 2R-f) = (R sin α)²

Aire de l'onglet : S = R²[ $α$ - sin(2. $α$ )/2] quand alpha est tout petit, on compare cette aire à celle de la parabole osculatrice 1/3 f.AB (théorème d'Archimède) : la différence est d'ordre supérieur à 3.

Formule de Machin (1706) : soit A l'arc dont la tangente est 1/5 et B celui dont l'arc est 1/239 : alors 4A -B = $π$ /4, ce qui donne une bonne approximation de Pi, "assez rapidement". Cette formule se généralise.

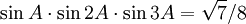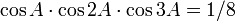Polygones réguliers constructibles : l'heptagone et le nonagone sont impossibles, mais le polygone à 17 côtés (heptadécagone) est constructible (théorème de Gauss à 19 ans : 1796) ; par contre on peut construire par pliage (cf origami) l'heptagone et le nonagone. On prouve néanmoins aisément que si A = 360°/7, alors $\sin{A}\cdot\sin{2A}\cdot\sin{3A}=\sqrt{7}/8$ et $\cos{A}\cdot\cos{2A}\cdot\cos{3A}=1/8$ . Des formules semblables existent pour le nonagone.

algorithme CORDIC de Briggs et redécouvert par Volker : ou comment votre calculette va-t-elle aussi vite ?

Voir aussi

Portail des mathématiques

Ce document provient de « Trigonom%C3%A9trie ».

Catégories : Angle | Trigonométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Trigométrie dans un triangle de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Dictionnaires et Encyclopédies sur 'Academic'

Trigométrie dans un triangle

Trigonométrie

Sommaire