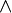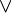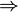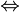- Treillis complet
-
Treillis (ensemble ordonné)
 Pour les articles homonymes, voir Treillis.
Pour les articles homonymes, voir Treillis.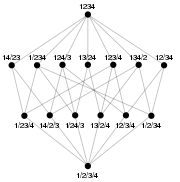 Le terme treillis provient de la forme du diagramme de Hasse associé à la relation d'ordre.
Le terme treillis provient de la forme du diagramme de Hasse associé à la relation d'ordre.
Un treillis (en anglais : lattice) est, en mathématiques, un ensemble partiellement ordonné dans lequel chaque couple d'éléments admet une borne supérieure et une borne inférieure. On parle aussi d'espace réticulé.
Il existe en réalité deux définitions équivalentes du treillis, une concernant la relation d'ordre citée précédemment, l'autre algébrique.
Sommaire
Définition algébrique
Un treillis est un ensemble E muni de deux lois internes habituellement notées
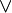 et
et  vérifiant :
vérifiant :- les deux lois sont commutatives et associatives
- pour tout a de E,
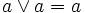 et
et 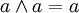 (idempotence)
(idempotence) - pour tout a et b de E:
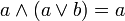 et
et 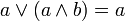 (absorption)
(absorption)
Pour démontrer que E est un treillis en tant qu'ensemble ordonné, il faut définir une relation d'ordre généralement notée
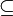 de la manière suivante :
de la manière suivante :On peut montrer que cette relation est bien une relation d'ordre (éventuellement partielle). La propriété d'associativité assure la transitivité. La propriété d'idempotence assure la réflexivité. La définition même assure l'antisymétrie. Grâce aux deux propriétés d'absorption, on peut aussi montrer que
On peut alors vérifier que,
Ce qui assure que (E ,
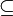 ) est bien un treillis au sens des ordres.
) est bien un treillis au sens des ordres.Définition par relation d'ordre
Un treillis est un ensemble E muni d'une relation d'ordre
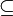 vérifiant, :
vérifiant, :- pour tous éléments a et b de E, il existe une borne supérieure et une borne inférieure à l'ensemble {a , b}
Pour montrer que E est un treillis algébrique, on remarque que la borne supérieure et la borne inférieure définissent alors deux lois internes :
Les propriétés de treillis algébrique pour ces deux lois découlent assez directement de la définition.
On définit donc indifféremment les treillis de façon algébrique ou par une relation d'ordre.
Exemples
- L'ensemble des parties d'un ensemble muni de l'inclusion forme un treillis où la borne supérieure est l'union et la borne inférieure l'intersection.
- Dans le même ordre d'idée, l'ensemble des ouverts d'un espace topologique (toujours muni de l'inclusion) forme un treillis. L'ensemble des ouverts réguliers (ouverts égaux à l'intérieur de leur adhérence) d'un espace topologique forme un treillis sans atomes (voir plus loin la définition d'atome).
- L'ensemble des entiers naturels muni de son ordre usuel est un exemple de treillis incomplet : il n'admet pas lui-même de borne supérieure.
- Soient f,g deux fonctions boréliennes sur R, intégrables pour la mesure de Lebesgue et vérifiant f<g. L'ensemble des fonctions boréliennes h comprises entre f et g est un treillis non complet qui devient complet si on identifie deux fonctions égales presque partout (attention ! la borne supérieure d'une famille de fonctions boréliennes peut être non mesurable ; lorsqu'on quotiente modulo l'égalité presque-partout, on regarde ce qu'on appelle une borne essentielle supérieure, laquelle, en revenant aux fonctions, majore presque-partout chaque élément de la famille).
Dualité
Si (E,
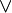 ,
,  , ≤) est un treillis, alors son treillis dual est (E,
, ≤) est un treillis, alors son treillis dual est (E,  ,
, 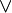 , ≥).
, ≥).Théorème de dualité : Si un théorème T est vrai pour tous les treillis alors le théorème dual de T, obtenu en remplaçant toutes les occurrences de
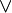 par
par  (et réciproquement) et toutes les occurrences de ≤ par ≥ (et réciproquement) est un théorème vrai pour tous les treillis.
(et réciproquement) et toutes les occurrences de ≤ par ≥ (et réciproquement) est un théorème vrai pour tous les treillis.Cas particuliers
Un ensemble ordonné dans lequel chaque couple d'éléments possède une borne supérieure (ou une borne inférieure) est un demi-treillis.
Un treillis E est complet si et seulement si pour tout sous-ensemble F de E, F possède une borne supérieure et une borne inférieure ; on dit aussi que E est un espace complètement réticulé.
Un treillis E est borné s'il possède un maximum et un minimum. En particulier tous les treillis complets sont bornés.
Si E est un treillis possédant un minimum que l'on note 0, un atome de E est un élément
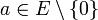 tel que pour tout
tel que pour tout 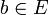 tel que
tel que 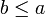 , on ait
, on ait 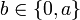 . Par exemple dans le treillis de l'ensemble des parties d'un ensemble, tous les singletons sont des atomes.
. Par exemple dans le treillis de l'ensemble des parties d'un ensemble, tous les singletons sont des atomes.Un treillis est distributif si et seulement si la loi
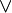 est distributive sur la loi
est distributive sur la loi  ou si la loi
ou si la loi  est distributive sur la loi
est distributive sur la loi 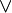 . En fait, les deux distributivités sont équivalentes, si un treillis en possède un type, il possède l'autre.
. En fait, les deux distributivités sont équivalentes, si un treillis en possède un type, il possède l'autre.Un treillis est complémenté s'il admet un plus petit élément noté 0, un plus grand élément noté 1, et si chacun de ses éléments x possède un complément y vérifiant
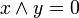 et
et 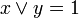 .
.Bibliographie
Ressources disponibles en ligne:
- Birkhoff, Garrett. Théorie et applications des treillis. Annales de l'institut Henri Poincaré, 11 no. 5 (1949), p. 227-240. [1]
- Burris, Stanley N., et Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.
- Jipsen, Peter, et Rose, Henry. Varieties of Lattices, Lecture Notes in Mathematics 1533, Springer Verlag, 1992. ISBN 0-387-56314-8.
Ouvrages de référence:
- Donnellan, Thomas, 1968. Lattice Theory. Pergamon.
- Grätzer, G., 1971. Lattice Theory: First concepts and distributive lattices. W. H. Freeman.
- Davey, B.A., et Priestley, H.A., 2002. Introduction to Lattices and Order. Cambridge University Press.
- Birkhoff, Garrett, 1967. Lattice Theory, 3rd ed. Vol. 25 of American Mathematical Society Colloquium Publications. American Mathematical Society.
Voir aussi
- Portail des mathématiques
Catégories : Structure algébrique | Théorie des ordres
Wikimedia Foundation. 2010.

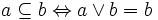
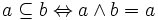
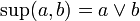
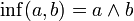
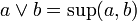
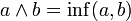
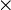
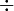

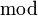
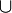
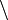
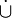
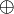
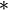
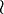 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit