Théorèmes de sylow

En théorie des groupes, les théorèmes de Sylow forment une réciproque partielle du théorème de Lagrange, d'après lequel, si H est sous-groupe d'un groupe fini G, alors l'ordre de H divise l'ordre de G. Un théorème de Sylow garantit, pour certains diviseurs de l'ordre de G, l'existence d'un sous-groupe d'ordre correspondant, et donne une information sur le nombre de ces sous-groupes.

Ils portent le nom du mathématicien norvégien Ludwig Sylow, qui les démontra en 1872.

Sommaire 1 Définition 2 Les théorèmes de Sylow 3 Exemples, applications 4 Démonstrations 5 Autres démonstrations 6 Voir aussi

Définition

Soit p un nombre premier; alors nous définissons un p-sous-groupe de Sylow de G comme un p-sous-groupe maximal de G (i.e., un sous-groupe qui est un p-groupe, et qui n'est un sous-groupe propre d'aucun autre p-sous-groupe de G). L'ensemble de tous les p-sous-groupes de Sylow pour un entier premier p donné est parfois noté Syl_p(G).

Les collections de sous-groupes maximaux, dans un sens ou un autre ne sont pas rares en théorie des groupes. Le résultat étonnant ici est que dans le cas de Syl_p(G), tous les membres sont en fait conjugués entre eux (et donc isomorphes) et cette propriété peut être exploitée pour déterminer d'autres propriétés de G.

Les théorèmes de Sylow

Les propositions suivantes furent avancées et démontrées par le mathématicien norvégien Ludwig Sylow en 1872. Soit G un groupe fini donné et p un nombre premier qui divise l'ordre de G, nous pouvons écrire l'ordre de G sous la forme (pⁿ · s), où n > 0 et p ne divise pas s. Alors:

• Il existe un p-sous-groupe de Sylow de G, d'ordre pⁿ.
• Tous les p-sous-groupes de Sylow de G sont conjugués entre eux (et ainsi sont isomorphes), i.e. si H et K sont des p-sous-groupes de Sylow de G, alors il existe un élément g dans G vérifiant g^-1H g = K.
• Soit n_p le nombre de p-sous-groupes de Sylow de G.
  • n_p divise s.
  • n_p = 1 mod p.

En particulier, les propriétés précédentes impliquent que tout p-sous-groupe de Sylow est du même ordre, pⁿ; et inversement, si un sous-groupe est d'ordre pⁿ, alors c'est un p-sous-groupe de Sylow, et ainsi est isomorphe à tous les autres p-sous-groupes de Sylow. À cause de la condition de maximalité, si H est un p-sous-groupe quelconque de G, alors H est un sous-groupe d'un p-sous-groupe d'ordre pⁿ.

Par ailleurs, le normalisateur de chaque p-Sylow de G est d'indice n_p dans G.

Exemples, applications

Soit G un groupe d'ordre 15 = 3 · 5. Nous devons avoir n₃ divise 5, et n₃ = 1 mod 3. La seule valeur satisfaisant ces contraintes est 1; ainsi, il y a un seul sous-groupe d'ordre 3, et il doit être normal (puisque il n'a pas de conjugués distincts). De façon analogue, n₅ divise 3, et n₅ = 1 mod 5; il a donc aussi un seul sous-groupe normal d'ordre 5. Puisque 3 et 5 sont premiers entre eux, l'intersection de ces deux sous-groupes est triviale, et donc G est nécessairement un groupe cyclique. Ainsi, il existe un seul groupe d'ordre 15 (à un isomorphisme près); noté .

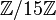Donnons un exemple plus complexe. Nous pouvons montrer qu'il n'y a pas de groupe simple d'ordre 350. Si |G| = 350 = 2 · 5² · 7, alors n₅ doit diviser 14 (= 2 · 7), et n₅ = 1 mod 5. Donc n₅ = 1 (puisque ni 6 ni 11 ne divisent 14), et ainsi G doit avoir un sous-groupe normal d'ordre 5², et donc ne peut pas être simple.

L'article groupe simple d'ordre 168 utilise un théorème de Sylow pour montrer le caractère simple d'un groupe. L'article groupe alterné utilise ces théorèmes pour montrer que le plus petit groupe simple non abélien est d'ordre 60.

Démonstrations

Les démonstrations des théorèmes de Sylow exploitent la notion d'action de groupe de diverses façons. Le groupe G agit sur lui-même ou sur l'ensemble de ses p-sous-groupes de différentes façons, et de telles actions peuvent être utilisées pour démontrer l'un des théorèmes de Sylow.

Les démonstrations reposent sur plusieurs propriétés des classes de conjugaison d'éléments et de sous-ensembles de G:

• |Cl(S)| = [G:N(S)]
  • où S est n'importe quel sous-ensemble de G, Cl(S) est la classe de conjugaison des ensembles T = g ^-1Sg pour une certaine g dans G, et N(S) est le normalisateur de S dans G.
• |Cl(x)| = [G:C(x)]
  • où x est élément quelconque de G, Cl(x) est la classe de conjugaison d'éléments y = g ^-1xg pour un certain g dans G, et C(x) est le centralisateur de x dans G.
• |G| = |Z(G)| + ∑_i [G:C(x_i)]
  • L' équation aux classes de G, où Z(G) est le centre de G, et la somme est prise sur un ensemble {x_i} représentant les classes de conjugaison de G non réduites à un singleton, cet-a-dire; non central.

D'abord, pour un groupe donné d'ordre pⁿ·s, nous pouvons démontrer par récurrence, que G a un sous-groupe K d'ordre pⁿ.

• Par récurrence sur l'ordre de G. Si G a un sous-groupe strict dont l'ordre est divisible par pⁿ alors, d'après l'hypothèse de récurrence, ce sous-groupe a un sous-groupe K d'ordre pⁿ; et, ainsi, il en est de même pour G.
• Supposons le contraire. Alors pour tout élément x qui n'est pas dans le centre de G, Z(G), nous obtenons que le centralisateur de x, C(x), est un sous-groupe strict de G; et ainsi son ordre ne sera pas divisible par pⁿ.
• D'après le théorème de Lagrange, |G| = |C(x)|·[G:C(x)]; puisque |G| est divisible par pⁿ, [G:C(x)] est divisible par p; ainsi comme nous l'avons remarqué précédemment, |Cl(x)| = [G:C(x)] est divisible par p.
• Donc, chaque |Cl(x_i)| dans l'équation aux classes est divisible par p, comme l'est |G|; il s'ensuit que, |Z(G)| est divisible par p. |Z(G)| est un groupe groupe abélien; et comme son ordre est divisible par p, il a un sous-groupe H d'ordre p (voir groupe abélien fini). En fait, H (qui est dans le centre de G) est un sous-groupe normal de G.
• Puisque H est normal, le groupe quotient G/H existe et aura un ordre divisible par p^n-1. D'après l'hypothèse de récurrence, G/H aura alors un sous-groupe L qui aura un ordre p^n-1.
• D'après le théorème des treillis, il existe un unique sous-groupe K de G tel que K/H = L; puisque H est d'ordre p, alors K est d'ordre pⁿ.

K est nécessairement maximal d'après Lagrange, donc est un p-sous-groupe de Sylow; et ainsi Syl_p(G) n'est pas vide.

Ensuite, nous utilisons l'existence de K pour démontrer que Cl(K), la classe de conjugaison de K, est en fait Syl_p(G); donc chaque p-sous-groupe de Sylow est un conjugué de K. En plus, cela démontre que n_p = 1 mod p.

• Pour l'affirmation suivante, soit H un p-sous-groupe de Sylow quelconque (pas nécessairement distinct de K). Nous pouvons partitionner Cl(K) en utilisant les automorphismes intérieurs induits par H de la manière suivante :
  • Étant donné L et M des éléments de Cl(K), M appartient à Cl(L) si et seulement s’il existe un h dans H tel que h ^-1Mh = L.
• Il est facile de voir que Cl'(L) est une classe d'équivalence; et que Cl(K) est la réunion disjointe de ces classes; ainsi |Cl(K)| = ∑_i(|Cl'(L_i)|), la somme des ordres de ces classes sur des représentants {L_i} sous-ensembles de Cl(K).
• Étant donnés a, b dans H, et un L dans Cl(K), a ^-1La = b ^-1Lb si et seulement si N_H(L)a = N_H(L)b, où N_H(L) est le normalisateur de L dans H.
• Donc |Cl'(L)| = [H:N_H(L)]. Remarquons que N_H(L) = (H ∩ N_G(L)); nous en déduisons que |Cl(L)| = [H:(H ∩ N(L))]. Puisque H est un p-groupe, (H ∩ N(L)) est aussi un p-groupe (d'après Lagrange); et ainsi pour tout L_i dans Cl(K), [H:(H ∩ N(L_i))] = |Cl'(L_i)| = p^m pour un m ≥ 0.
• À ce point, il serait intéressant d'en savoir un peu plus sur (H ∩ N(L_i)). Donnons nous un L quelconque dans Cl(K), considérons un élément x dans H, où x n'est pas dans L. Alors x n'est pas dans N(L), et ainsi H ≠ (H ∩ N(L)):
  • Supposons que x soit dans N(L). Rappelons que L est un sous-groupe normal de N(L), et considérons l'élément xL/L du groupe quotient N(L)/L.
  • Puisque H est un p-groupe, x^q = e, où q est une puissance de p. Donc, nous devons avoir que xL/L a un ordre divisant une puissance de p. Mais puisque |L| = pⁿ, p ne peut pas diviser |N(L)/L|; et ainsi xL/L est l'élément neutre de N(L)/L. Ainsi x doit être un élément de L; et donc un élément de N(L), contrairement à l'hypothèse.
• Donc, si L appartient à Cl(K) et si H ≠ L, alors |Cl'(L)| = [H:(H ∩ N(L))] = p^m pour un certain m>0. D'un autre côté, si H = L appartient à Cl(K), alors |Cl'(L)| = |Cl'(H)| = [H:(H ∩ N(H))] = [H:H] = 1.
• Puisque Cl(K) est la réunion disjointe des Cl'(L_i), |Cl(K)| = kp pour un certain k si H n'est pas dans Cl(K), et |Cl(K)|=kp+1 si H est dans Cl(K).
• Nous avions avancé au début que H n'était pas nécessairement distinct de K. Puisque K appartient à Syl_p(G), nous pouvons prendre H = K pour montrer que |Cl(K)| = 1 mod p; en même temps, ceci fournit une contradiction si nous supposons que H n'est pas dans Cl(K) (comme son ordre ne peut pas être à la fois égal à 0 et 1 mod p).
• Donc H est dans Cl(K), et ainsi Syl_p(G) = Cl(K).
• Tout p-sous-groupe de Sylow est conjugué K; et n_p = |Cl(K)| = 1 mod p.

L'autre fait concernant n_p suit presque immédiatement.

• Puisque n_p = 1 mod p, n_p ne divise pas pⁿ; puisque n_p = [G : N(K)], il divise |G|, ains’il doit diviser s.

---

Remarquons que l'argument utilisé ci-dessus concernant la conjugaison reste valable aussi longtemps que |Cl(K)| = [G:N(K)] est fini; ainsi nous pouvons énoncer de façon analogue des théorèmes de Sylow pour les groupes infinis :

• Si K est un p-sous-groupe de Sylow de G, et n_p = |Cl(K)| est fini, alors tout p-sous-groupe de Sylow est conjugué à K, et n_p = 1 mod p.

Autres démonstrations

Premier théorème

On suppose 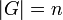(i.e. G d'ordre n) ; alors 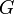est isomorphe à un sous-groupe de 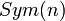qui est isomorphe à un sous-groupe de 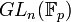qui est l'ensemble des applications linéaires d'un 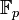-espace vectoriel 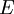de dimension 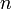. Soit 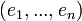une base de 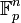, comme 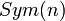est l'ensemble des permutations d'un ensemble à 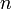éléments, par exemple 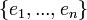, si 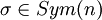, 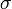permute la base, donc on peut lui faire correspondre une application linéaire bijective, i.e. un élément de 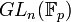. 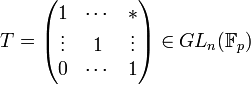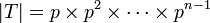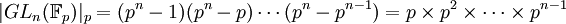Soit , et et 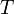est un sous-groupe de 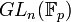, donc 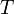est un 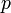-sous-groupe de Sylow de 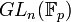et comme 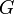est isomorphe à un sous-groupe de 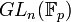, 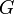admet un 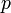-sous-groupe de Sylow

Voir aussi

Sous-groupe de Hall

• Portail des mathématiques