- Théorème du sandwich au jambon
-
En mathématiques, le théorème du sandwich au jambon en dimension trois s'exprime de façon imagée en disant qu'on peut couper en quantités égales, d'un seul coup de couteau, le jambon, le fromage et le pain d'un sandwich[1]. Il se formalise et se généralise en dimension quelconque. Ce théorème, qu'Hugo Steinhaus avait conjecturé dans le Scottish Book, a été aussitôt démontré en 1938 par Stefan Banach à l'aide du théorème de Borsuk-Ulam[2].
Énoncé
Étant données n parties[3] Lebesgue-mesurables et de mesures finies d'un espace euclidien de dimension n, il existe au moins un hyperplan affine divisant chaque partie en deux sous-ensembles de mesures égales[1].
Démonstration
Soient
 les n parties
les n parties  , de mesures finies
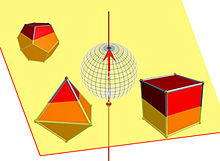
, de mesures finies  , que l'on souhaite couper en deux parties d'égale mesure (en dimension n = 3, la figure illustre la preuve, avec pour
, que l'on souhaite couper en deux parties d'égale mesure (en dimension n = 3, la figure illustre la preuve, avec pour  , des solides de Platon en orange et rouge).
, des solides de Platon en orange et rouge).Ayant fixé un vecteur x de la sphère Sn − 1, on considère, pour tout réel t, l'hyperplan affine orthogonal à x passant par tx, et le demi-espace délimité par cet hyperplan et contenant (t + 1)x. Le volume Vi(t,x) de l'intersection de Ai et de ce demi-espace est une fonction continue de (t,x) et vérifie :

Comme de plus
 est une fonction décroissante de t, qui tend vers 0 quand t tend vers
est une fonction décroissante de t, qui tend vers 0 quand t tend vers  et vers V1 quand t tend vers
et vers V1 quand t tend vers  , l'ensemble des réels t tels que V1(t,x) = V1 / 2 est un segment non vide [t'(x),t''(x)] qui vérifie [t'( − x),t''( − x)] = [ − t''(x), − t'(x)]. Son milieu
, l'ensemble des réels t tels que V1(t,x) = V1 / 2 est un segment non vide [t'(x),t''(x)] qui vérifie [t'( − x),t''( − x)] = [ − t''(x), − t'(x)]. Son milieu  est donc une fonction continue impaire de x vérifiant V1(t(x),x) = V1 / 2 pour toute direction x.
est donc une fonction continue impaire de x vérifiant V1(t(x),x) = V1 / 2 pour toute direction x.Par composition, la fonction
est également continue. On peut donc lui appliquer le théorème de Borsuk-Ulam, ce qui fournit une direction x telle que f(x) = f( − x). Pour un tel x, l'hyperplan orthogonal à x et passant par t(x)x coupe les Ai pour
 en deux morceaux de même mesure car
en deux morceaux de même mesure carAinsi, Vi(t(x),x) = Vi / 2 est vrai pour
 par choix de x et pour i = 1 par définition de t(x). Ceci achève la preuve.
par choix de x et pour i = 1 par définition de t(x). Ceci achève la preuve.Notes et références
- (en) Jiří Matoušek (de), Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry, Springer, 2003 (ISBN 978-3-54000362-5), p. 47
- (en) W. A. Beyer et Andrew Zardecki, « The early history of the ham sandwich theorem », dans Amer. Math. Monthly, vol. 111, 2004, p. 58–61
- Les n parties ne sont pas supposées connexes : dans le sandwich, les deux tranches de pain constituent une partie.
Wikimedia Foundation. 2010.