- Théorème des quatre carrés de lagrange
-
Théorème des quatre carrés de Lagrange
Le théorème des quatre carrés de Lagrange, aussi connu sous le nom de conjecture de Bachet et démontré en 1770 par le mathématicien français Joseph Louis Lagrange correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. Il s'énonce de la façon suivante :
Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que :
Le mathématicien français Adrien-Marie Legendre améliora le théorème en 1798 en affirmant qu'un entier positif peut être exprimé comme la somme d'au plus trois carrés si et seulement s'il n'est pas de la forme
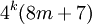 .
.
Sa démonstration était incomplète, laissant une brèche qui fut comblée plus tard par le mathématicien allemand Carl Friedrich Gauss.
Le théorème des quatre carrés de Lagrange est un cas particulier du théorème du nombre polygonal de Fermat et du problème de Waring.
La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler :
Fonctions arithmétiques
Les fonctions arithmétiques permettent d'obtenir des résultats plus généraux. Si on pose r4(n) comme étant le nombre de façon de décomposer n sous forme d'une somme de 4 carrés, on obtient le résultat suivant:
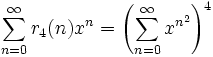 , pour | x | < 1.
, pour | x | < 1.
Moyennant l'utilisation des séries de Lambert, on en déduit le théorème suivant, dit théorème de Jacobi :
- Portail des mathématiques
Catégories : Équation diophantienne | Théorème d'algèbre | Joseph-Louis Lagrange | Arithmétique modulaire
Wikimedia Foundation. 2010.

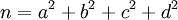
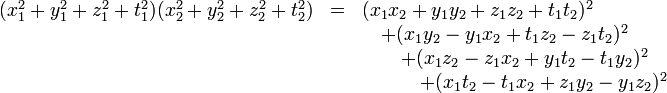
![\forall n \in \mathbb{N}^*, \ r_4(n) = 8 \sum_{d|n, d \not\equiv 0[4]}{d}](/pictures/frwiki/102/f2de8fa897b940dd87bfb7457bc12e72.png)