Théorème de wilson

Théorème de wilson

Théorème de Wilson

Alhazen (965 - 1039) est le premier mathématicien connu pour avoir énoncé le théorème de Wilson.

En mathématiques, et plus précisément, en arithmétique élémentaire, le Théorème de Wilson énonce une relation entre la fonction factorielle et une congruence modulo un nombre premier.

Il est utilisé pour résoudre des équations diophantiennes. Un exemple est donné par Leonhard Euler (1707 – 1783) dans sa démonstration du théorème des deux carrés de Fermat.

Ce théorème doit son nom à John Wilson (1741 – 1793) qui a conjecturé ce résultat à la fin du XVIIIe siècle.

Sommaire

Énoncé et exemples

Énoncé

Théorème de Wilson — Un entier p strictement plus grand que 1, est un nombre premier si et seulement s'il divise (p - 1)! + 1, c'est-à-dire si et seulement si :

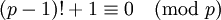
(p-1)!+1 \equiv 0 \pmod p \;

Ici, le symbole ! désigne la fonction factorielle et le symbole 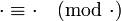\cdot \equiv \cdot \pmod \cdot désigne la congruence sur les entiers.

Remarque : La formule précédente est équivalente à :

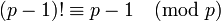
(p-1)! \equiv p-1 \pmod p \;

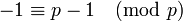
car : -1\equiv p-1 \pmod p \;

Exemples

  • Si p est égal à 3, alors (p - 1)! + 1 est égal à 3, un multiple de 3.
  • Si p est égal à 4, alors (p - 1)! + 1 est égal à 7 qui n'est pas multiple de 4.
  • Si p est égal à 5, alors (p - 1)! + 1 est égal à 25, un multiple de 5.
  • Si p est égal à 6, alors (p - 1)! + 1 est égal à 121 qui n'est pas multiple de 6.
  • Si p est égal à 17, alors (p - 1)! + 1 est égal à 20 922 789 888 001, un multiple de 17 car 17 x 1 230 752 346 353 = 20 922 789 888 001.

Histoire

Le premier texte à faire référence[1] à ce résultat est énoncé par le mathématicien arabe Alhazen (965 - 1039), démontrant une remarquable avance sur les sciences occidentales. Ce théorème est connu à partir du XVIIe siècle en Europe. Gottfried Wilhelm von Leibniz (1646 - 1716) fait référence à ce résultat. Euler le prouve[2] et l'utilise [3] pour sa démonstration du théorème des deux carrés de Fermat. Leibniz ne semble pas avoir jugé nécessaire de publier une preuve.

John Wilson redécouvre ce qu'il croit être une conjecture et en partage la découverte avec son professeur Edward Waring (1736 – 1798) qui publie ce résultat[4] en 1770. Une démonstration est présentée[5] comme nouvelle l'année suivante, elle est due à Joseph-Louis Lagrange (1736 – 1813).

La formalisation[6] des techniques de l'arithmétique modulaire de Carl Friedrich Gauss (1777 - 1855) permet une démonstration plus simple[7]. C'est elle, ou une analogue qui est maintenant généralement présentée.

Démonstrations

Arithmétique modulaire

Une démonstration moderne se fonde sur les propriétés de l'arithmétique modulaire[8]. Si p est un nombre premier, le corps Z/pZ a une structure connue, c'est celle d'un corps fini.

Le principe consiste, à regrouper deux à deux dans Z/pZ*, les éléments avec leurs inverses. Cette technique n'est possible que si un élément α de Z/pZ* est différent de son inverse, autrement dit si, et seulement si, α2 est différent de 1. Les éléments différents de leurs inverses sont racine du polynôme X2 - 1. Ce polynôme est à coefficients dans un corps et est égal à l'expression suivante (X - 1)(X + 1), ce qui revient à dire que les deux seuls éléments qui sont leurs propres inverses sont la classe de 1 et celle de -1, encore égal à p - 1. Autrement dit, il existe exactement (p - 3)/2 couples distincts composés d'un élément de Z/pZ* et de son inverse différent du premier élément du couple. Il existe aussi deux classes, celle de 1 et celle de p - 1, qui sont leurs propres inverses. Dans Z/pZ*, le calcul de la classe du produit de tous les éléments de Z/pZ*, qui correspond à la classe de (p - 1)! est le produit des produits des deux membres des (p - 3)/2 couples, égal à 1 par 1 puis par -1, qui est bien congru à -1 modulo p. Ce qui démontre le résultat.

Si p n'est pas un nombre premier, la démonstration est assez facile, et ne nécessite pas l'usage de l'arithmétique modulaire. Soit p n'est pas un carré parfait et il existe deux entiers distincts a et b, strictement plus petits que p, tels que le produit de a et de b soit égal à p. Comme a et b sont deux facteurs de (p - 1)!, cette valeur est un multiple de p, ce qui montre que (p - 1)! est un multiple de p et que théorème ne peut pas être vérifiée. Ainsi, 5! est égal à 120, un multiple de 6. Si p est un carré parfait différent de 1 et de 4, noté a2, alors a et 2.a sont deux facteurs de (p - 1)! et on conclut comme précédemment. On vérifie bien que 8!, égal à 40 320 est bien un multiple de 9. Il ne reste que le cas où p est égal à 4, qui se vérifie manuellement.

Principe de la démonstration de Gauss

Gauss raisonne de manière un peu plus astucieuse[7]. Il remarque que le groupe multiplicatif Z/pZ* est cyclique, c'est à dire engendré par une classe a particulière. Ainsi, Z/7Z* est engendré par 3, car les puissances de 3 ont pour classes respectives 3, 2, 6, 4, 5, 1. Calculer la congruence de (p - 1)!, c'est à dire le produit de tous les éléments de Z/pZ*, revient par l'isomorphisme de groupe de (Z/pZ*, .) dans (Z/(p-1)Z, +) à calculer la somme de 1 à p - 1.

Pour calculer la somme de 1 à p - 1, on remarque qu'il est possible d'ajouter 0 en première position, alors le ième terme s'annule avec le p - 1 - ième.

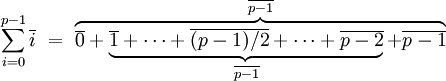
\sum_{i=0}^{p-1}\overline i \ = \ \overbrace{\overline 0+\underbrace{\overline 1+\cdots + \overline {(p-1)/2} + \cdots + \overline {p-2}}_{\overline {p-1}} + \overline {p-1} }^{\overline {p-1}}

Comme p est impair, la somme contient un nombre impair de termes, il ne reste plus que (p - 1)/2, l'unique élément d'ordre deux. Dans Z/pZ*, l'unique élément d'ordre 2 est -1, ce qui termine la démonstration.

Gauss ne raisonne pas exactement ainsi, il remarque qu'il existe un élément a générateur du groupe Z/pZ*, ce qui revient à dire que les p - 1 premières puissances de a forment les éléments du groupe et donc que la congruence de (p - 1)! est égal à celle des produits de ces différentes puissance, encore égal à une puissance de a. Plus précisément :

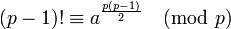
(p-1)! \equiv a^{\frac{p(p-1)}2} \pmod p

Il remarque ensuite que a(p-1)/2 est un nombre dont le carré est congru à 1 modulo p car ap-1 est congru à 1 modulo p. En effet, a engendre un groupe multiplicatif d'ordre p - 1. Comme l'ordre du groupe engendré par a est p - 1, a(p-1)/2 ne peut être congru à 1, sinon a serait d'ordre (p - 1)/2. La seule congruence différente de 1 et dont le carré est congru à 1 est -1, donc a(p-1)/2 est congru à -1, modulo p. Si p est un nombre impair, la valeur a(p-1)/2 à la puissance p est aussi congru à -1. Si p est un nombre pair, il est égal à 2 car c'est l'unique nombre pair premier et l'on vérifie manuellement que le théorème est encore vérifié. Ce qui termine le raisonnement de Gauss.

Démonstration manuelle

Alhazen, Leibniz ou Euler ne disposent pas de ce savoir. Ils connaissent la division euclidienne, le théorème des restes chinois et son équivalent algébrique le théorème de Bachet-Bézout enfin des propriétés décrites dans l'article Congruence sur les entiers à l'exception du dernier paragraphe.

Une démonstration est toujours possible, elle est en revanche plus longue et plus astucieuse. L'abstraction de l'approche modulaire est remplacée par une complexité plus grande. Celle présentée ici dérive de l'approche de Gauss[9]


Démonstration sans les outils de l'arithmétique modulaire
  • Si p n'est pas premier, p ne divise pas (p - 1)! + 1.

En effet, si p n'est pas premier, il admet un diviseur d compris entre 2 et p-1, que l'on retrouve dans un des facteurs de (p - 1)!. Si l'on suppose que p divise (p - 1)! + 1 alors d divise l'entier (p - 1)! et son successeur : c'est une contradiction.

  • Si p est premier alors la division de (p - 1)! par p donne pour reste moins un.

Procédons en plusieurs étapes. Dans un premier temps, l'objectif est de montrer que si a est un entier compris entre 1 et p - 1, il existe un entier b aussi compris entre 1 et p - 1 tel que la division euclidienne de a.b par p possède pour reste 1.

Il existe deux entiers positifs b1 et q1 tel que :
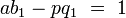
ab_1 - pq_1 \ = \ 1

En effet, le théorème de Bachet-Bézout montre l'existence de deux entiers b2 et q2 tel que a.b2 + p.q2 = 1. Si b2 est positif, la proposition est démontrée, sinon il existe un entier positif m tel que b1 = b2 + m.p soit strictement positif car l'ensemble des entiers est archimédien. On définit q1 par l'égalité q1 = q2 - m.p. Le couple b1 et q1 vérifie bien les hypothèses de la proposition.

Il existe un unique entier b compris entre 1 et p - 1 vérifiant la proposition suivante :
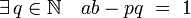
\exists \, q \in \mathbb N \quad ab - pq \ = \ 1

Il suffit, pour se persuader de son existence, de diviser b1 par p, si b est le reste d'une telle division, il correspond à la valeur recherchée.

Montrons l'unicité, si β1 et β2 sont deux valeurs vérifiant la proposition et tel que β1 est supérieur ou égal à β2, alors a.(β1 - β2) est un multiple de p, le lemme d'Euclide permet alors de conclure que β1 - β2 est nul, ce qui démontre l'unicité.

La deuxième étape consiste à regrouper les différents entiers a et b par paires. Les produits a.b donnent tous pour reste par la division euclidienne par p la valeur 1, et les produits de ces produits donnent encore 1 pour reste de la même division euclidienne. Cette propriété est démontrée dans le paragraphe Structure d'anneau de l'article Congruence sur les entiers, et étaient connues des différents mathématiciens ayant travaillé sur ce théorème.

Il reste néanmoins encore une difficulté, correspondant aux cas ou les valeurs a et b sont égales.

Les seules valeurs de a tel que a est égal à b sont 1 et p - 1.

Si a est b sont égaux, alors il existe un entier q tel que : a 2 - 1 = p.q. On reconnait une identité remarquable et :

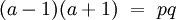
(a-1)(a+1) \ = \ pq \;

Le lemme d'Euclide permet alors de conclure que a est égal à 1 ou à p - 1.

Conclusion

En réordonnançant les différents facteurs de (p - 1)!, on obtient des paires d'entiers dont le produit possède pour reste 1 par la division euclidienne par p et 1 et p - 1, ce qui montre que le reste de la division euclidienne de (p - 1)! par p est égal à p - 1.

Si l'utilisation des notations des congruences simplifie l'exposé, la complexité reste essentiellement la même. En revanche la connaissance de la structure du groupe multiplicatif simplifie grandement la démonstration.

Généralisation

Dans un groupe abélien fini le produit des éléments est égal

  • au neutre si son ordre est impair
  • au produit des involutions ( éléments d'ordre 2 ) si son ordre est pair.

Pour le groupe 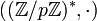((\mathbb Z/p\mathbb Z)^*, \cdot), avec p premier impair, on retrouve le version classique.

En effet, l'ordre, qui est égal à p − 1, est pair et l'unique involution est p − 1.

Notes et références

Notes

  1. ↑ Alhazen Opuscula
  2. ↑ Leonhard Euler Opusc. Anal. Tome 1 p 329
  3. ↑ G. Van Brummelen M. Kinyon Mathematics and the Historian’s Craft Springer New York 2005
  4. ↑ Edward Waring Edward Waring Meditationes Cambridge J. Archdeacon 1770
  5. ↑ Joseph-Louis Lagrange Démonstration d'un théorème nouveau concernant les nombres premiers Nouv. Mem. de l'Académie des sciences et belles lettres S 125-137 1771
  6. ↑ Carl Friedrich Gauss , Disquisitiones arithmeticae, 1801 Traduction M. Poullet-Delisle Ed. Courcier 1807
  7. ↑ a  et b  Carl Friedrich Gauss, Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Ed. Courcier p 55 1807
  8. ↑ Celle proposée ici s'inspire de : S. Mehl Démonstration du théorème de Wilson par le site Chronomath.com
  9. ↑ La démonstration proposée ici est classique, on la trouve posée sous forme d'exercice avec la correction par le site maths-express.com

Liens externes

Références

  • D Weeks Meditationes algebraicae Traduction anglaise des travaux d'Edward Waring Providence RI, 1991
  • R Rashed, Entre arithmétique et algèbre: Recherches sur l'histoire des mathématiques arabes Paris, 1984
  • Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Wilson ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de wilson de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Theoreme de Wilson — Théorème de Wilson Alhazen (965 1039) est le premier mathématicien connu pour avoir énoncé le théorème de Wilson. En mathématiques, et plus précisément, en arithmétique élémentaire, le Théorème de Wilson énonce une relation entre la fonction… …   Wikipédia en Français

  • Théorème de Wilson — Alhazen (965 1039) est le premier mathématicien connu pour avoir énoncé le théorème de Wilson. En mathématiques, plus précisément en arithmétique élémentaire, le théorème de Wilson énonce qu un entier p plus grand que 1 est premier si et… …   Wikipédia en Français

  • Wilson — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Étymologie historique 2 Patronyme 3 …   Wikipédia en Français

  • Theoreme de Stokes — Théorème de Stokes Pour les articles homonymes, voir Stokes. Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de stokes — Pour les articles homonymes, voir Stokes. Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de Wick — Le théorème de Wick est un outil particulièrement important de la physique statistique, dans la mesure où il permet de calculer des valeurs moyennes d observables compliquées, par exemple des corrélations ou des interactions à plusieurs… …   Wikipédia en Français

  • Théorème de Stokes — Pour les articles homonymes, voir Stokes. En géométrie différentielle, le théorème de Stokes est un résultat central sur l intégration de formes différentielles, qui généralise nombre de théorèmes sur l analyse vectorielle. Après l énoncé et la… …   Wikipédia en Français

  • Wilson's theorem — In mathematics, Wilson s theorem states that a natural number n > 1 is a prime number if and only if (see factorial and modular arithmetic for the notation). Contents 1 History 2 Proofs …   Wikipedia

  • John Wilson (mathématicien) — Pour les articles homonymes, voir Wilson. John Wilson (1741–1793) est un mathématicien britannique qui a conjecturé un théorème, dont il ignorait qu il était déjà connu mais qui porte aujourd hui son nom : le théorème de Wilson. John Wilson… …   Wikipédia en Français

  • Nombre De Wilson — En mathématiques, un nombre premier de Wilson est une certaine catégorie de nombre premier. Un nombre premier p est appelé un nombre premier de Wilson si divise , où ! désigne la fonction factorielle ; comparer ceci avec le théorème de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”