Théorème de tychonov

Théorème de tychonov: Théorème de Tychonov

Le théorème de Tychonov est un théorème de topologie qui affirme qu'un produit d'espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï Nikolaïevitch Tikhonov. Il a plusieurs applications en topologie algébrique et différentielle, particulièrement en analyse fonctionnelle, pour la preuve du théorème de Banach-Alaoglu-Bourbaki et le compactifié de Stone-Čech.

Si ce théorème ne choque pas l'intuition dans le cas d'un produit fini, sa validité dans le cas d'un produit quelconque est plus étonnante, et se démontre par une méthode non constructive faisant appel à l'axiome du choix. On notera qu'il est aussi possible de se passer de l'axiome du choix dans le cas d'un produit dénombrable d'espaces métriques compacts, ce que nous montrons dans la première partie de cet article, la deuxième étant consacrée à la démonstration dans le cas général.

Sommaire

1 Démonstration dans le cas d'un produit dénombrable de métriques

2 Démonstration dans le cas général

3 Remarque

4 Equivalence avec l'axiome du choix

5 Notes

6 Voir aussi

Démonstration dans le cas d'un produit dénombrable de métriques

Dans le cas du produit dénombrable de métriques, l'idée essentielle est de faire de ce produit un espace lui aussi métrique en le munissant d'une distance appropriée, ce qui permet ensuite d'utiliser le théorème de Bolzano-Weierstrass: le produit X sera compact si et seulement si de toute suite d'éléments de X on peut extraire une sous-suite convergente.

Démonstration

Soit donc 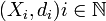$(X_i,d_i)i\in\mathbb{N}$ une famille de métriques compacts. On se ramène à des distances $d i$ plus petites que 1: pour chaque $i$ , la distance $d' i = M i n (d i,1)$ définit la même topologie que la distance $d i$ . Définissons sur 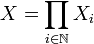$X=\prod_{i\in\mathbb{N}}X_i$ l'application $d$ par: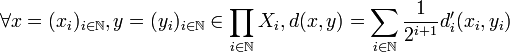

$\forall x=(x_i)_{i\in\mathbb{N}}, y=(y_i)_{i\in\mathbb{N}} \in \prod_{i\in\mathbb{N}}X_i, d(x,y)=\sum_{i\in\mathbb{N}}\frac{1}{2^{i+1}}d'_i(x_i,y_i)$

On vérifiera aisément que c'est bien une distance sur $X$ . Montrons qu'elle définit les mêmes ouverts de la topologie produit.

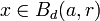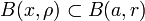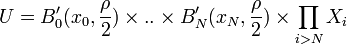Soit $x\in B_d(a,r)$ , montrons que x appartient à un ouvert pour la topologie produit contenu dans $B d (a, r)$ . Par l'inégalité triangulaire, il existe $ρ > 0$ tel que $B(x,\rho)\subset B(a,r)$ . La série $\sum \frac{1}{2^{i+1}}$ est absolument convergente: son reste tend donc vers 0. Soit donc $N$ tel que $\sum_{i\ge N}\frac{1}{2^{i+1}}<\frac{\rho}{2}$ . 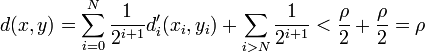On considère alors l'ouvert $U=B'_0(x_0,\frac{\rho}{2})\times ..\times B'_N(x_N,\frac{\rho}{2})\times\prod_{i>N}X_i$ , si $y\in U$ alors $d(x,y)=\sum_{i=0}^N \frac{1}{2^{i+1}}d'_i(x_i,y_i) +\sum_{i> N}\frac{1}{2^{i+1}} < \frac{\rho}{2}+\frac{\rho}{2}=\rho$ donc $U$ voisinage au sens de la topologie produit de $x$ inclus dans $B d (a, r)$ : la topologie produit contient donc la topologie métrique.

Réciproquement, soit U ouvert de la topologie produit, soit 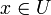$x\in U$ , alors il existe 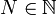$N\in \mathbb{N}$ et $r 0 .. r N > 0$ tels que 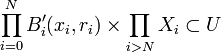$\prod_{i=0}^{N} B'_i(x_i,r_i)\times\prod_{i>N}X_i \subset U$ . 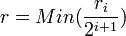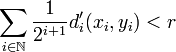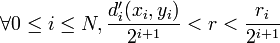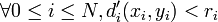On considère alors le rayon $r=Min(\frac{r_i}{2^{i+1}})$ : la boule pour $d$ de centre $x$ et de rayon r est alors incluse dans $U$ : en effet si $d (x, y) < r$ , alors $\sum_{i\in\mathbb{N}} \frac{1}{2^{i+1}}d'_i(x_i,y_i)<r$ , comme la somme est à termes positifs chaque terme est donc plus petit que r: $\forall 0\le i\le N, \frac{d'_i(x_i,y_i)}{2^{i+1}}<r<\frac{r_i}{2^{i+1}}$ donc $\forall 0\le i\le N, d'_i(x_i,y_i)<r_i$ , donc $y\in u$ . 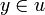U est donc voisinage de chacun de ses points au sens de la topologie métrique: c'est donc un ouvert de la topologie métrique: la topologie métrique contient la topologie produit.

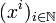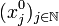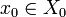Ainsi, la topologie métrique et la topologie produit sont égales. On peut alors utiliser pour la compacité de $X$ la caractérisation séquentielle par un procédé diagonal: soit $(x^i)_{i\in\mathbb{N}}$ une suite d'éléments de X (une suite de suites). La suite $(x^0_j)_{j\in\mathbb{N}}$ admet une suite extraite $(x^0_{n_0(j)})_{j\in\mathbb{N}}$ qui converge vers $x_0\in X_0$ par compacité de $X 0$ . 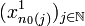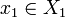Alors la suite $(x^1_{n_0(j)})_{j\in\mathbb{N}}$ admet une suite extraite $(x^1_{n_1(j)})_{j\in\mathbb{N}}$ qui converge vers $x_1\in X_1$ par compacité de $X 1$ , et $n 1$ est une sous suite de $n 0$ donc 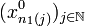$(x^0_{n_1(j)})_{j\in\mathbb{N}}$ converge vers $x 0$ . 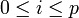Par récurrence, supposons qu'il existe une extractrice $n p$ telle que pour tout $0\le i\le p$ , $(x^i_{n_p(j)})_{j\in\mathbb{N}}$ converge vers $x i$ . 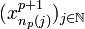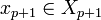$(x^{p+1}_{n_{p}(j)})_{j\in\mathbb{N}}$ suite d'éléments de $X p + 1$ , donc admet une sous suite $(x^{p+1}_{n_{p+1}(j)})_{j\in\mathbb{N}}$ convergeant vers $x_{p+1}\in X_{p+1}$ , avec $n p + 1$ extraite de $n p$ , ce qui prouve la récurrence, or la propriété est vérifiée pour p=0 donc par récurrence on a l'existence d'éléments $x i$ tels que pour tout $p$ , il existe une extractrice $n p$ avec que pour tout 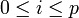$0\le i\le p$ , $(x^i_{n_p(j)})_{j\in\mathbb{N}}$ converge vers $x i$ .

L'extractrice 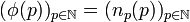$(\phi(p))_{p\in\mathbb{N}}=(n_p(p))_{p\in\mathbb{N}}$ donne alors une suite extraite de 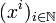$(x^i)_{i\in\mathbb{N}}$ qui converge vers 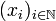$(x_i)_{i\in\mathbb{N}}$ par construction, ce qui achève la preuve puisqu'on est dans un métrique.

Démonstration dans le cas général

On va utiliser la propriété de Borel-Lebesgue pour les fermés: un espace $X$ est compact si seulement si il est séparé et pour toute famille 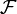$\mathcal{F}$ de fermés de $X$ dont l'intersection finie d'éléments est non vide, alors: 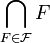$\bigcap_{F \in \mathcal{F}} F$ est non vide. Comme tout produit de séparés est séparé pour la topologie produit, il reste à prouver que le produit de compacts vérifie la propriété de Borel-Lebesgue, et ce en utilisant le lemme de Zorn.

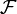Soit donc $(X_\alpha)_{\alpha \in A}$ une famille de compacts, et soit $\mathcal{F}$ une famille de fermés de 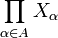$\prod_{\alpha \in A} X_\alpha$ dont l'intersection finie d'éléments est non vide. On notera $p α$ la projection sur $X α$ .

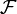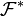On va considérer l'ensemble des familles contenant (au sens de l'inclusion) $\mathcal{F}$ et dont les intersections finie d'éléments sont non vides: c'est un ensemble ordonné par l'inclusion et inductif: il vérifie donc les hypothèses du lemme de Zorn, et admet donc un élément maximal $\mathcal{F}^*$ .

Soit 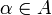$\alpha \in A$ fixé. Comme l'intersection finie d'éléments de 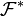$\mathcal{F}^*$ est non vide, c'est aussi le cas de l'intersection finie de projections sur $X α$ d'éléments de 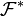$\mathcal{F}^*$ , donc de l'adhérence de tels éléments: ainsi la famille 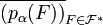$\overline {(p_\alpha(F))}_{F\in \mathcal{F}^*}$ vérifie les hypothèses de la propriété de Borel-Lebesgue dans $X α$ compact, donc 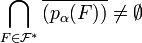$\bigcap_{F\in \mathcal{F}^*} \overline {(p_\alpha(F))} \ne \empty$ : soit donc $x α$ élément de cette intersection.

On va alors considérer l'élément 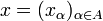$x=(x_\alpha)_{\alpha \in A}$ du produit et montrer qu'il est bien dans l'intersection des éléments de 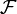$\mathcal{F}$ , qui sera alors non vide ce qui achèvera la preuve.

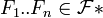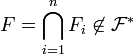On remarque tout d'abord que par maximalité, (L1): $\mathcal{F}*$ est stable par intersection finie: sinon il existe $F_1..F_n \in \mathcal{F}*$ tels que $F=\bigcap_{i=1}^n F_i \not\in \mathcal{F}^*$ , alors l'intersection d'éléments de 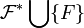$\mathcal{F}^*\bigcup \{F\}$ est non vide, et il contient 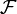$\mathcal{F}$ tout en étant strictement plus grand que 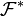$\mathcal{F}^*$ : absurde par maximalité de celui-ci.

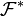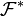Par un argument similaire, on en déduit que (L2): si un ensemble intersecte tous les éléments de $\mathcal{F}^*$ , alors il appartient à $\mathcal{F}^*$ .

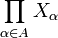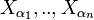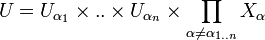Soit $U$ ouvert de $\prod_{\alpha \in A} X_\alpha$ contenant $x$ : il existe $U_{\alpha_1} , .., U_{\alpha_n}$ ouverts respectifs de $X_{\alpha_1},.., X_{\alpha_n}$ tels que $U=U_{\alpha_1} \times .. \times U_{\alpha_n}\times \prod_{\alpha \ne \alpha_{1..n}}X_\alpha$ .

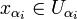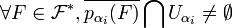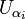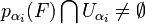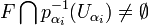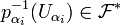Alors soit $1\le i\le n$ , on a $x_{\alpha_i} \in U_{\alpha_i}$ , ainsi $\forall F \in \mathcal{F}^*, \overline{p_{\alpha_i}(F)} \bigcap U_{\alpha_i}\ne \empty$ , or $U_{\alpha_i}$ ouvert donc $p_{\alpha_i}(F) \bigcap U_{\alpha_i}\ne \empty$ , donc $F \bigcap p_{\alpha_i}^{-1}(U_{\alpha_i})\ne \empty$ . Alors par (L2), $p_{\alpha_i}^{-1}(U_{\alpha_i})\in\mathcal{F}^*$ .

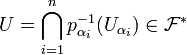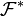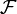Donc par (L1), $U=\bigcap_{i=1}^n p_{\alpha_i}^{-1}(U_{\alpha_i})\in\mathcal{F}^*$ , donc $U$ intersecte tous les éléments de $\mathcal{F}^*$ , a fortiori de $\mathcal{F}$ .

Ainsi x est dans l'adhérence de tous les éléments de 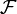$\mathcal{F}$ qui sont fermés, donc x appartient à tous les éléments de 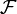$\mathcal{F}$ dont l'intersection est donc non vide, ce qui achève la preuve.

Remarque

On peut donner une démonstration élégante ^[1] de ce théorème en utilisant la théorie des filtres

Equivalence avec l'axiome du choix

Nous avons précedemment évoqué l'équivalence du théorème de Tychonov avec l'axiome du choix. Cette équivalence, bien qu'a priori surprenante, se comprend mieux en remarquant que l'on peut définir une topologie sur un ensemble quelconque. En l'occurrence, nous allons utiliser une légère variante de la topologie cofinie, qui possède une propriété très intéressante: tout espace est compact pour la topologie cofinie.

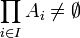Soit donc $(A_i)_{i\in I}$ une famille d'ensemble, nous voulons montrer $\prod_{i\in I} A_i \ne \empty$ . On suppose, quitte à réindexer par un ensemble $I'$ que 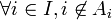$\forall i \in I, i\not\in A_i$ . Alors, on pose 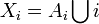$X_i=A_i\bigcup {i}$ , et on munit $X i$ de la topologie $τ i$ formée de l'ensemble vide, de tous les ensembles de complémentaire fini, et du singleton ${i}$ (On vérifiera qu'on a alors bien une topologie, et que $X i$ est alors compact). Par Tychonov, le produit $X$ des $X i$ est compact.

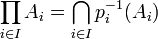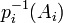On remarque que, en notant $p i$ la projection sur $X i$ , on a: $\prod_{i\in I} A_i =\bigcap_{i\in I} p_i^{-1}(A_i)$ . Or X est compact: pour montrer que $\bigcap_{i\in I} p_i^{-1}(A_i)\ne\empty$ on va se servir de la contraposée de la propriété de Borel-Lebesgue pour les fermés: si chaque $p_i^{-1}(A_i)$ est fermé et que toute intersection finie de 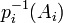$p_i^{-1}(A_i)$ est non vide, alors l'intersection des 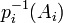$p_i^{-1}(A_i)$ est non vide, ce qui achèvera la preuve.

Or 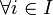$\forall i \in I$ comme $A i$ est le complémentaire de ${i}$ ouvert, $A i$ est fermé. Donc par continuité de la projection $p i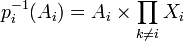$ , $p_i^{-1}(A_i)=A_i\times\prod_{k\ne i} X_i$ est fermé. De plus soit 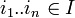$i_1..i_n\in I$ , alors $\bigcap_{k=1}^n p_{i_k}^{-1}(A_{i_k})=A_{i_1}\times ..\times A_{i_n} \times \prod _{i\not\in \{i_1..i_n\}}X_i$ qui est non vide: en effet en choisissant $a 1 .. a n$ éléments respectifs de $A 1 .. 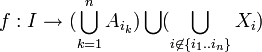A n$ on peut définir $f:I\rightarrow (\bigcup_{k=1}^n A_{i_k})\bigcup (\bigcup_{i\not\in \{i_1..i_n\}}X_i)$ par $f (i 1) = a 1 .. f (i n) = a n$ et $f (i) = i$ si $i\not\in\{i_1..i_n\}$ : on a donc bien la propriété annoncée.

Notes

↑ Olivier Brinon, LE THEOREME DE TYCHONOFF

Voir aussi

Théorème de Tychonov dans les ensembles flous

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Tychonov ».

Catégories : Théorème de mathématiques | Compacité

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de tychonov de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Theoreme de Tychonov — Théorème de Tychonov Le théorème de Tychonov est un théorème de topologie qui affirme qu un produit d espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï… … Wikipédia en Français
Théorème de Tychonov — Le théorème de Tychonov est un théorème de topologie qui affirme qu un produit d espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï Nikolaïevitch Tikhonov. Il a… … Wikipédia en Français
Théorème de Tychonoff — Théorème de Tychonov Le théorème de Tychonov est un théorème de topologie qui affirme qu un produit d espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï… … Wikipédia en Français
Theoreme d'Ascoli — Théorème d Ascoli En analyse fonctionnelle, le théorème d Ascoli est un puissant résultat caractérisant les parties relativement compactes de l espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se … Wikipédia en Français
Théorème d'Arzelà-Ascoli — Théorème d Ascoli En analyse fonctionnelle, le théorème d Ascoli est un puissant résultat caractérisant les parties relativement compactes de l espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se … Wikipédia en Français
Theoreme de Banach-Alaoglu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Théorème de Banach-Alaoglu — Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie… … Wikipédia en Français
Théorème de Banach-Alaoğlu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Théorème de banach-alaoglu — Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie… … Wikipédia en Français
Théorème de Borel-Lebesgue — Ne doit pas être confondu avec Théorème de Borel. En topologie de , le théorème de Borel Lebesgue ou de Heine Borel établit l équivalence entre les deux propriétés suivantes d un ensemble A de vecteurs : A est fermé et borné (A est … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts