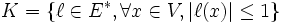Théorème de Banach-Alaoglu
- Théorème de Banach-Alaoglu
-
Théorème de Banach-Alaoglu-Bourbaki
Le théorème de Banach-Alaoglu-Bourbaki est un résultat de compacité en analyse fonctionnelle.
Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par
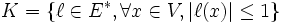
est une partie compacte pour la topologie faible-*.
La démonstration du théorème fait intervenir le Théorème de Tychonov.
Il résulte de ce théorème que si E est un espace vectoriel normé, la boule unité de l'espace dual (muni de la norme de la topologie forte) est *-faiblement compacte.
Dans un espace de Banach réflexif (en particulier un espace de Hilbert) toute suite bornée admet une sous-suite faiblement convergente.
Références
- Walter Rudin, Analyse fonctionnelle [détail des éditions]
Liens externes
 Portail des mathématiques
Portail des mathématiques
Catégories : Espace vectoriel topologique | Espace de Hilbert | Théorème de mathématiques | Compacité
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Banach-Alaoglu de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme de Banach-Alaoglu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Théorème de Banach-Alaoğlu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Théorème de banach-alaoglu — Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie… … Wikipédia en Français
Théorème de Banach-Alaoglu-Bourbaki — Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie faible *.… … Wikipédia en Français
Theoreme de Banach-Schauder — Théorème de Banach Schauder En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces… … Wikipédia en Français
Théorème de banach-schauder — En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces vectoriels normés complets est … Wikipédia en Français
Theoreme de Banach-Steinhaus — Théorème de Banach Steinhaus Le théorème de Banach Steinhaus (aussi appelé Principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn Banach et le théorème de Banach Schauder, des résultats fondamentaux de l analyse… … Wikipédia en Français
Théorème de banach-steinhaus — Le théorème de Banach Steinhaus (aussi appelé Principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn Banach et le théorème de Banach Schauder, des résultats fondamentaux de l analyse fonctionnelle. Il a été publié en… … Wikipédia en Français
Theoreme de Banach-Mazur — Théorème de Banach Mazur Le théorème de Banach Mazur est un outil d analyse fonctionnelle. De manière très approximative, il exprime que les espaces vectoriels normés vérifiant des conditions raisonnables du point de vue de l analyse sont des… … Wikipédia en Français
Théorème de banach-mazur — Le théorème de Banach Mazur est un outil d analyse fonctionnelle. De manière très approximative, il exprime que les espaces vectoriels normés vérifiant des conditions raisonnables du point de vue de l analyse sont des sous espaces fermés de l… … Wikipédia en Français