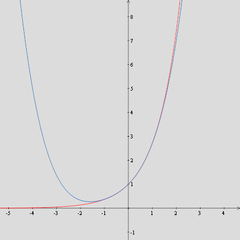
Théorème de Taylor-Lagrange

Théorème de Taylor

Pour les articles homonymes, voir Taylor.

En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l'établit en 1712, permet l'approximation d'une fonction plusieurs fois dérivable au voisinage d'un point par une fonction polynôme dont les coefficients dépendent uniquement des dérivées de la fonction en ce point.

On pose pour l'article :

I est un intervalle de 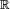$\scriptstyle\R$ , non vide et non réduit à un point.
E un espace vectoriel normé de dimension finie.

De manière plus précise : si $n$ est un entier naturel et $f$ définie sur I à valeur dans E, alors pour tout 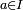$\scriptstyle a\in I$ telle que $f (n) (a)$ existe,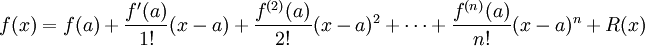

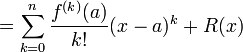
$f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \frac{f^{(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R(x)$ $= \sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x - a)^k + R(x)$

La fonction exponentielle (en rouge) et le polynôme de Taylor d'ordre 4 au point 0 (en bleu)

Ici, $n!$ désigne la factorielle de $n$ , et $R (x)$ est un reste qui dépend de $x$ et est d'autant plus petit que $x$ est proche de $a$ .

Lorsque la formule de Taylor est appliquée avec $a = 0$ , on l'appelle formule de Mac Laurin.

Sommaire

1 Traitement du reste
2 Formule de Taylor pour les fonctions de plusieurs variables
3 Sources
4 Articles connexes

Traitement du reste

Taylor ne s'est pas vraiment préoccupé de la forme du reste, il faut attendre ses successeurs pour voir se développer une maîtrise du reste dans certaines conditions plus précises.

On pose dans la suite 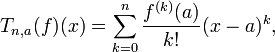$T_{n,a}(f)(x)=\sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k,$ de sorte que la formule devient $f (x) = T n, a (f)(x) + R (x).$

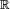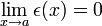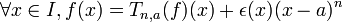
Formule de Taylor-Young : Soit f une fonction à valeurs dans E définie sur un intervalle I contenant le réel a, et possédant en a une dérivée nième (n entier strictement positif) Alors il existe une fonction $ε$ définie sur I et à valeurs dans $\scriptstyle \R$ vérifiant $\lim_{x\to a}\epsilon (x)=0$ et telle que : $\forall x\in I, f(x)=T_{n,a}(f)(x)+\epsilon(x)(x-a)^n$
Formule de Taylor-Lagrange : pour une fonction n + 1 fois dérivable sur I
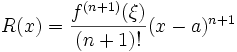
- $R(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} (x-a)^{n+1}$
  où $ξ$ est un nombre compris strictement entre $a$ et $x$
- S'il existe M tel que 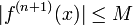$|f^{(n+1)}(x)| \leq M$ pour tout $x$ de $I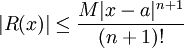$ : $|R(x)| \leq \frac{M|x-a|^{n+1}}{(n+1)!}$ (inégalité de Taylor-Lagrange)
Formule de Taylor avec reste de Laplace (ou reste intégral) : pour une fonction n+1 fois continûment dérivable sur I
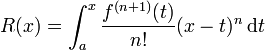
- $R(x) = \int_a^x \frac{f^{(n+1)} (t)}{n!} (x - t)^n \,\mathrm dt$
- l'inégalité de Taylor-Lagrange peut aussi être obtenue à partir de cette expression
Formule de Taylor-Maclaurin : lorsque $a = 0$ , la formule devient plus simple

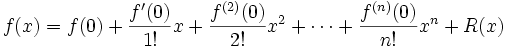
$f(x) = f(0) + \frac{f'(0)}{1!}x + \frac{f^{(2)}(0)}{2!}x^2 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + R(x)$

Si $R$ est exprimé sous la seconde forme, appelée forme de Lagrange, le théorème de Taylor représente une généralisation du théorème des accroissements finis (qui peut être utilisé pour démontrer cette version), tandis que la troisième expression de $R$ montre que le théorème est une généralisation du théorème fondamental du calcul différentiel et intégral (qui est utilisé dans la démonstration de cette version).

Pour certaines fonctions $f$ , nous pouvons montrer que le reste $R$ tend vers zéro quand $n$ tend vers l'infini ; ces fonctions peuvent être développées en série de Taylor dans un voisinage du point $a$ et sont appelées des fonctions analytiques.

Le théorème de Taylor (avec reste intégral) est aussi valable si la fonction $f$ est à valeurs complexes ou dans un espace vectoriel. Ce n'est pas le cas de l'égalité de Taylor-Lagrange.

Démonstration de la formule de Taylor avec reste intégral

Montrons le résultat par récurrence sur $n$ .

La propriété est vraie au rang 0. En effet, selon le théorème fondamental de l'analyse on a bien que si $f$ est de classe 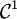$\mathcal{C}^1$ sur $[a, x]$ alors: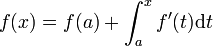

$f(x)=f(a)+\int_a^xf'(t)\mathrm{d}t$

Supposons la formule vraie au rang $n$ . Alors pour $f$ de classe 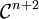$\mathcal{C}^{n+2}$ sur $[a, x]$ on obtient, par intégration par parties:

$\begin{align} \int_a^x \frac{(x-t)^n}{n!} f^{(n+1)}(t)\mathrm{d}t &= \left[-\frac{(x-t)^{n+1}}{(n+1)!}f^{(n+1)}(t)\right]_a^x-\int_a^x -\frac{(x-t)^{n+1}}{(n+1)!}f^{(n+2)}(t)\mathrm{d}t \\ &= \frac{(x-a)^{n+1}}{(n+1)!}f^{(n+1)}(a)+\int_a^x \frac{(x-t)^{n+1}}{(n+1)!}f^{(n+2)}(t)\mathrm{d}t \end{align}$

Et comme par hypothèse de récurrence

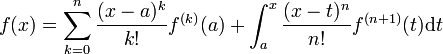
$f(x)=\sum_{k=0}^n \frac{(x-a)^k}{k!}f^{(k)}(a)+\int_a^x \frac{(x-t)^n}{n!} f^{(n+1)}(t)\mathrm{d}t$

on obtient :

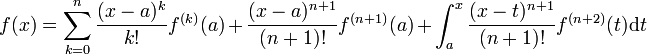$f(x)=\sum_{k=0}^n \frac{(x-a)^k}{k!}f^{(k)}(a)+\frac{(x-a)^{n+1}}{(n+1)!}f^{(n+1)}(a)+\int_a^x \frac{(x-t)^{n+1}}{(n+1)!}f^{(n+2)}(t)\mathrm{d}t$ .

On obtient

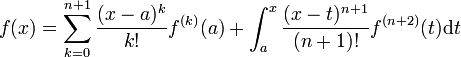$f(x)=\sum_{k=0}^{n+1} \frac{(x-a)^k}{k!}f^{(k)}(a)+\int_a^x \frac{(x-t)^{n+1}}{(n+1)!} f^{(n+2)}(t)\mathrm{d}t$ ,

ce qui montre que notre propriété est vraie au rang $n + 1$ .∎

Démonstration de la formule de Taylor-Young pour une fonction de classe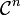 $\mathcal{C}^n$

Nous reprenons f, a et b telles que définies dans l'énoncé de la formule de Taylor-Young.

Pour $n = 0$ , on a 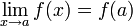$\lim_{x\to a}f(x)=f(a)$ car f est continue en a. D'où $\forall x\in[a,b], f(x)=f(a)+\underbrace{(f(x)-f(a))}_{\to 0 \mbox{ lorsque } x\to a}\cdot (x-a)^0$

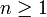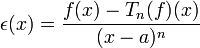Pour $n\geq 1$ , Pour $x\in]a,b]$ , on pose $\epsilon(x)=\frac{f(x)-T_n(f)(x)}{(x-a)^n}$ .

On pose $ε(a) = 0$ .

On a bien $\forall x\in[a,b], f(x)=T_n(f)(x)+\epsilon(x)(x-a)^n$

On introduit la fonction g définie sur $[a, b]$ par $\forall x\in[a,b],g(x)=f(x)-\frac{(x-a)^n}{n!}f^{(n)}(a)$

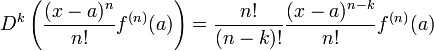
- Pour $k\in[0..n-1]$ , $g (k) (a) = f (k) (a)$ car $D^k\left(\frac{(x-a)^n}{n!}f^{(n)}(a)\right)=\frac{n!}{(n-k)!}\frac{(x-a)^{n-k}}{n!}f^{(n)}(a)$
- $g (n) (a) = 0$

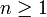
On a donc $g\in\mathcal{C}^n([a,b],\R)$ avec $n\geq 1$

En appliquant la formule de Taylor avec reste intégral à l'ordre n-1, on obtient $\forall x\in[a,b], g(x)=\sum^{n-1}_{k=0}\frac{(x-a)^k}{k!}g^{(k)}(a)+\int^x_a\frac{(x-t)^{n-1}}{(n-1)!}g^{(n)}(t)\mathrm{d}t$

On remarque par ailleurs que $\forall x\in[a,b], f(x)-T_n(f)(x)=g(x)-\sum^{n-1}_{k=0}\frac{(x-a)^k}{k!}g^{(k)}(a)$

On a ensuite : soit $ε > 0$ , il existe $\eta\in]0,b-a[$ tel que $\forall t\in[a,a+\eta], |g^{(n)}(t)|\leq\epsilon$

Alors $\forall x\in[a, a+\eta], \left|\int_a^x\frac{(x-t)^{n-1}}{(n-1)!}g^{(n)}(t)\mathrm{d}t\right|\leq\epsilon\int_a^x\frac{(x-t)^{n-1}}{(n-1)!}\mathrm{d}t=\epsilon\frac{(x-a)^n}{n!}$

D'où $\forall x\in[a, a+\eta], \left|\epsilon(x)\right|\leq\frac{\epsilon}{n!}$

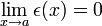Donc $\lim_{x\to a}\epsilon(x)=0$ ∎

Démonstration de la formule de Taylor-Lagrange

Nous allons prouver la formule de Taylor-Lagrange directement, par application du théorème de Rolle.

Pour tout réel x de l'intervalle I, on introduit la fonction définie par

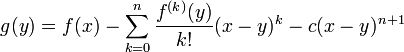
$g(y) = f(x) - \sum_{k = 0}^n \frac{f^{(k)}(y)}{k!}(x-y)^k - c (x - y)^{n+1}$

où $c$ est choisi de telle façon que $g (a) = 0$ , c'est-à-dire :

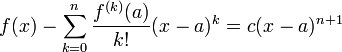$f(x) - \sum_{k = 0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k = c (x - a)^{n+1}$ .

Il est clair, vu la définition de $g$ , que $g (x) = 0$ .

Vu les hypothèses de la formule, nous pouvons appliquer le théorème de Rolle pour trouver $ξ$ entre $a$ et $x$ tel que $g'(ξ) = 0$ .

Comme

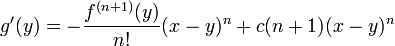
$g'(y) = -\frac{f^{(n+1)}(y)}{n!}(x -y)^{n} + c (n+1)(x -y)^n$ ,

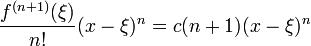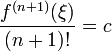nous voyons que : $\frac{f^{(n+1)}(\xi)}{n!}(x -\xi)^{n} = c (n+1)(x - \xi)^n$ soit $\frac{f^{(n+1)}(\xi)}{(n+1)!} = c$ qui implique :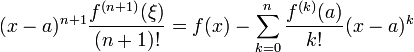

$(x-a)^{n+1} \frac{f^{(n+1)}(\xi)}{(n+1)!} = f(x) - \sum_{k = 0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k$

qui est bien la formule proposée.

Formule de Taylor pour les fonctions de plusieurs variables

Il existe des formules analogues pour des fonctions n fois différentiables en 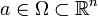$a\in\Omega\subset\R^{n}$ à valeur dans 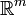$\R^{m}$ mais l'expression est assez lourde compte tenu des coefficients multinomiaux qui interviennent.

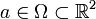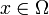En particulier, pour une fonction $f$ , $2$ -fois différentiable en $a\in\Omega\subset\R^2$ à valeur dans $\R$ , on peut écrire pour tout $x\in\Omega$ :

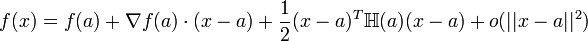
$f(x) = f(a)+\nabla f(a) \cdot (x-a) + \frac{1}{2}(x-a)^T \mathbb{H}(a) (x-a)+ o(||x-a||^{2})$

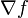où $\nabla f$ est le gradient de $f$ et 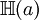$\mathbb{H}(a)$ est la matrice Hessienne de $f$ évaluée en $a$ .

Exemple :

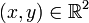
Soit une fonction $f$ 2-fois différentiable en $(a, b)$ à valeur dans $\R$ , alors pour tout $(x,y)\in\R^{2}$

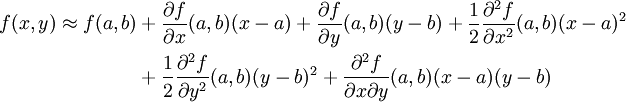
$\begin{align} f(x,y)\approx f(a,b) &+ \frac{\partial f}{\partial x}(a,b) (x-a) + \frac{\partial f}{\partial y}(a,b) (y-b) + \frac{1}{2}\frac{\partial^2 f}{\partial x^2}(a,b)(x-a)^2\\ &+ \frac{1}{2}\frac{\partial^2 f}{\partial y^2}(a,b)(y-b)^2 + \frac{\partial^2 f}{\partial x \partial y}(a,b)(x-a)(y-b) \end{align}$

Sources

J. Lelong Ferrand et J-M Arnaudiès, Cours de mathématiques (T2 : Analyse), Bordas (1977)
Claude Deschamps et André Warusfel, J'intègre: Mathématiques première année, Dunod (1999)

Articles connexes

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Taylor ».

Catégories : Théorème d'analyse | Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Taylor-Lagrange de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Taylor-Lagrange — Théorème de Taylor Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par … Wikipédia en Français
Theoreme de Taylor — Théorème de Taylor Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par … Wikipédia en Français
Théorème de taylor — Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par une fonction… … Wikipédia en Français
Théorème de Taylor — Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1715[1], montre qu une fonction plusieurs fois dérivable au voisinage d un point peut être approximée par une… … Wikipédia en Français
Formule de Taylor-Lagrange — Théorème de Taylor Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par … Wikipédia en Français
Taylor-Young — Théorème de Taylor Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par … Wikipédia en Français
TAYLOR (B.) — TAYLOR BROOK (1685 1731) Mathématicien anglais, né à Edmonton et mort à Londres, célèbre pour ses contributions au développement du calcul infinitésimal. Taylor fit ses études au collège Saint John, à Cambridge, et étudia les mathématiques sous… … Encyclopédie Universelle
Lagrange — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronymes 1.1 Lagrange 1.2 … Wikipédia en Français
Théorème de Glaeser — Le théorème de Glaeser, en analyse mathématique, est une caractérisation de la continuité de la dérivée de la racine carrée des fonctions de classe C2. Il a été publié en 1963 par Georges Glaeser[1], puis simplifié par Jean Dieudonné[2]. Énoncé… … Wikipédia en Français
Développement de Taylor — Théorème de Taylor Pour les articles homonymes, voir Taylor. En analyse, le théorème de Taylor, du nom du mathématicien Brook Taylor qui l établit en 1712, permet l approximation d une fonction plusieurs fois dérivable au voisinage d un point par … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Taylor-Lagrange