Théorème d'Al-Kashi

Fig. 1 - Notations usuelles dans un triangle quelconque.

Le théorème d'Al-Kashi, en France, loi des cosinus dans les autres pays francophones et dans d'autres langues, ou encore théorème de Pythagore généralisé, est un théorème de géométrie couramment utilisé en trigonométrie, qui relie dans un triangle la longueur d'un côté à celles des deux autres et au cosinus de l'angle formé par ces deux côtés. Il généralise ainsi le théorème de Pythagore aux triangles non rectangles. Le nom francisé du mathématicien perse Ghiyath al-Kashi (1380 - 1429) lui a été attribué en France dans les années 1990, les appellations théorème de Pythagore généralisé ou loi des cosinus étant utilisées jusque-là.

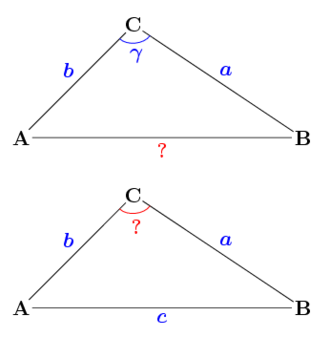
Le théorème d'al-Kashi s'énonce de la façon suivante :

Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure 1 : d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les longueurs des côtés respectivement opposés à ces angles.

$c^2 = a^2 + b^2 - 2ab\ \cos\ \gamma.$

Sommaire

1 Histoire
2 Le théorème et ses applications
3 Démonstrations
4 Généralisation aux géométries non euclidiennes
- 4.1 Géométrie sphérique
- 4.2 Géométrie hyperbolique
5 Généralisation à l'espace euclidien
6 Notes et références
7 Voir aussi

Histoire

Fig. 2 - Triangle ABC avec hauteur BH.

Les Éléments d'Euclide datant du III^e siècle av. J.‑C., contenaient déjà une approche géométrique de la généralisation du théorème de Pythagore : les propositions 12 et 13 du livre II, traitent séparément le cas d'un triangle obtusangle et celui d'un triangle acutangle. La formulation de l'époque est pédestre, car l'absence de fonction trigonométrique et d'algèbre oblige à raisonner en termes de différences d'aires. Aussi la proposition 12 utilise-t-elle ces termes :

« Dans les triangles obtusangles, le carré du côté qui soutient l'angle obtus est plus grand que la somme des carrés des deux autres côtés, de la quantité de deux fois le rectangle formé d'un des côtés contenant l'angle obtus, à savoir celui sur le prolongement duquel tombe la hauteur, et de la ligne prise en dehors entre [le pied de] la hauteur et l'angle obtus. »

— Euclide, Les Éléments^[1]

En notant ABC le triangle d'angle obtus A et H le pied de la hauteur issue de B (cf. Fig. 2 ci-contre), les notations modernes permettent de résumer l'énoncé ainsi :

AB² = CA² + CB² + 2 CA CH.

Il fallut attendre la trigonométrie arabo-musulmane au Moyen Âge pour voir le théorème évoluer dans sa forme et dans sa portée : l'astronome et mathématicien al-Battani généralisa le résultat d'Euclide à la géométrie sphérique au début du X^e siècle^[2], ce qui permit d'effectuer des calculs de distance angulaire entre étoiles. C'est durant la même période que se sont établies les premières tables trigonométriques, pour les fonctions sinus et cosinus. Cela permit à Ghiyath al-Kashi, mathématicien de l'école de Samarcande, de mettre le théorème sous une forme utilisable pour la triangulation au cours du XV^e siècle. La propriété a été popularisée en occident par François Viète qui l'a, semble-t-il, redécouverte indépendamment^[3].

C'est au début du XIX^e siècle que les notations algébriques modernes permettent d'écrire le théorème sous sa forme actuelle et qu'il prend dans de nombreuses langues le nom de loi (ou théorème) des cosinus.

Le théorème et ses applications

Le théorème d'Al-Kashi est également connu sous le nom de théorème de Pythagore généralisé^[4], car le théorème de Pythagore en est un cas particulier :

L'angle

γ

est droit (autrement dit lorsque cos γ = 0) si et seulement si $c^2=a^2+b^2, \,$ d'après le théorème d'Al-Kashi.

Fig. 3 - Utilisation du théorème d'Al-Kashi : angle ou côté inconnu.

Le théorème s'utilise en triangulation (voir Fig. 3) pour résoudre un triangle, à savoir déterminer

le troisième côté d'un triangle dont on connaît un angle et les côtés adjacents :

$c = \sqrt{a^2+b^2-2ab\cos\gamma}; \,$

les angles d'un triangle dont on connaît les trois côtés :

$\gamma = \arccos \dfrac{a^2+b^2-c^2}{2ab}.$

Ces formules sont instables numériquement dans le cas de triangles en épingle, c'est-à-dire lorsque c est petit devant a et b — ou, de façon équivalente, lorsque γ est petit devant 1.

Il existe un corollaire du théorème d'al-Kashi : pour deux triangles directement semblables ABC et A'B'C'

$cc' = aa' + bb' - (ab'+a' b)\cos \gamma. \,$

Démonstrations

Tout comme le théorème de Pythagore, le théorème d'Al-Kashi possède de nombreuses démonstrations, certaines utilisant des propriétés sur les aires comme celles d'Euclide ou d'Al-Kashi, d'autres utilisant des propriétés trigonométriques ou liées au cercle. Enfin, le théorème d'Al-Kashi peut être vu comme une application des propriétés sur le produit scalaire^[5].

Démonstration d'Euclide

Fig. 4 - Démonstration du théorème d'Al-Kashi pour un angle obtus : « selon Euclide ».

La démonstration d'Euclide^[6] par la proposition 12 (angle obtus) et 13 (angle aigu) s'appuie sur le théorème de Pythagore et fait intervenir le point H pied de la hauteur issue de B. Pour Euclide cette propriété est une propriété sur des aires. Pour l'angle obtus (proposition 12), Euclide remarque que

$CH^2+CA^2+2\times CH \times AC=AH^2$

Il lui suffit alors d'ajouter l'aire du carré de côté HB

$HB^2 + CH^2 + CA^2+2\times CH \times AC=AH^2+ HB^2$

et d'utiliser le théorème de Pythagore

$CB^2+CA^2 + 2\times CH \times CA= AB^2$

Une démonstration analogue est réalisable pour l'angle aigu.

Démonstration d'Al-Kashi

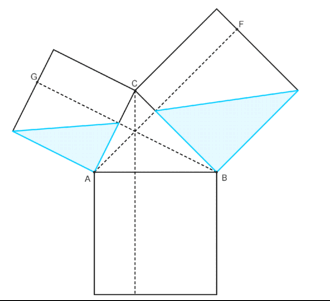
Fig. 5 - Démonstration du théorème d'Al-Kashi pour un triangle acutangle : « selon Al-Kashi ».

Dans son livre Clé de l'arithmétique en 1429^[7], Al-Kashi généralise le théorème de Pythagore et introduit dans l'égalité la trigonométrie. Pour lui aussi, cette propriété est liée aux aires. Ainsi dans un triangle aigu ABC, il mène par A et par B les hauteurs du triangle qui découpent dans les carrés s'appuyant sur CB et CA des rectangles. La somme des aires des rectangles de diagonales BF et AG correspond à l'aire du carré sous AB et les rectangles de diagonales CF et CG ont une même aire égale à CB × CA × cos(C) Ce qui donne effectivement

$CA^2+CB^2=AB^2+2 CB\times CA \times \cos(C)$

Une démonstration analogue est envisageable pour un triangle obtusangle en opérant par soustraction d'aires.

Par un découpage d'aires

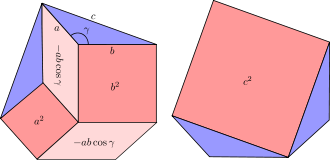
Fig. 6a - Démonstration du théorème d'Al-Kashi pour les triangles à angles aigus : « méthode du découpage ».

Fig. 6b - Démonstration du théorème d'Al-Kashi dans le cas d'un angle obtus : « méthode du découpage »

Un certain nombre des démonstrations du théorème font intervenir un calcul d'aires^[8]. Il convient en effet de remarquer que

$a 2$ , $b 2$ et $c 2$ sont les aires de carrés de côtés respectifs $a$ , $b$ et $c$ ;
$a b | cos γ |$ est celle d'un parallélogramme de côtés $a$ et $b$ formant un angle $π / 2 - γ$ , le changement de signe de $cos γ$ lorsque l'angle $γ$ devient obtus rendant une étude par cas obligatoire.

La figure 6a (ci-contre) découpe un heptagone de deux manières différentes de sorte à démontrer le théorème d'Al-Kashi dans le cas d'un angle aigu. Interviennent :

en rose, les aires $a 2$ , $b 2$ à gauche, et les aires $2 a b cos γ$ et $c 2$ à droite ;
en bleu, le triangle ABC, à droite comme à gauche ;
en gris, quelques triangles supplémentaires, identiques au triangle ABC et en même nombre dans les deux découpages.

L'égalité des aires de droite et de gauche donne

$\,a^2+b^2 = c^2+2ab \cos\gamma$ .

La figure 6b (ci-contre) découpe un hexagone de deux manières différentes de façon à démontrer le théorème d'Al-Kashi dans le cas d'un angle obtus. La figure montre

en rose, les aires $a 2$ , $b 2$ et $- 2 a b cos γ$ à gauche, et l'aire $c 2$ à droite ;
en bleu, deux fois le triangle ABC, à droite comme à gauche.

L'égalité des aires à droite et à gauche donne

$\,a^2+b^2-2ab\cos\gamma = c^2$ .

Une démonstration rigoureuse nécessiterait de prouver que les deux découpages sont effectivement identiques, ce qui utilise principalement les cas d'égalité des triangles.

Par le théorème de Pythagore

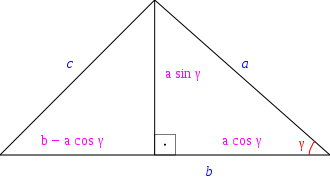
Fig. 7 - Démonstration du théorème d'Al-Kashi en utilisant les relations trigonométriques.

La figure 7 (ci-contre) indique la manière de procéder pour démontrer le théorème d'Al-Kashi dans le cas d'un triangle à angles aigus en utilisant le théorème de Pythagore sur un sous-triangle rectangle formé en prenant le pied de la hauteur^[9] . Seule la dernière étape n'est pas indiquée sur la figure : le théorème de Pythagore s'applique au triangle rectangle dont le côté c est l'hypoténuse :

$\,c^2 = (a\sin\gamma)^2 + (b-a\cos\gamma)^2$ ,

ce qui donne le résultat escompté, après simplification.

La méthode est en tous points similaire pour les angles obtus.

En utilisant la puissance d'un point par rapport à un cercle

Fig. 8 - Démonstration du théorème d'Al-Kashi en utilisant la puissance d'un point par rapport à un cercle.

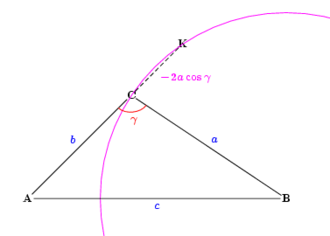
On considère le cercle de centre B et de rayon [BC] (cf. figure ci-contre). Il coupe la droite (AC) en C et K. La puissance du point A par rapport au dit cercle est :

$\mathrm{AB}^2 - \mathrm{BC}^2 = \overline{\mathrm{AC}}\cdot\overline{\mathrm{AK}} = \overline{\mathrm{AC}}\cdot(\overline{\mathrm{AC}}+\overline{\mathrm{CK}})$

d'où

$c^2-a^2 = b\,(b-2a\ \cos\ \gamma)$ .

Contrairement aux précédentes, pour cette démonstration, il n'est pas nécessaire de recourir à une étude par cas. En effet, les mesures algébriques permettent de traiter pareillement un angle aigu ( $\overline{\mathrm{CK}} < 0$ ) et un angle obtus ( $\overline{\mathrm{CK}} > 0$ ).

On trouve trace de l'utilisation de la puissance d'un point par rapport à un cercle pour déterminer tous les angles d'un triangle dont les longueurs sont connues, dans l'œuvre de Nicolas Copernic, Des révolutions des sphères célestes. Il présente ainsi deux algorithmes l'un utilisant le théorème de Pythagore généralisé présent dans l'œuvre d'Euclide^[10], l'autre utilisant la puissance d'un point par rapport à un cercle^[11].

Ainsi dans une figure analogue à celle ci-contre, il fait remarquer que, a et c étant connu, la puissance du point A par rapport au cercle tracé est connue

en langage mathématique actuel, elle vaut

c 2 - a 2

Il en déduit que, puisque b est connu, AK est connu

en effet $AK \times b = c^2-a^2$ donc $AK=\frac{c^2-a^2}{b}$

Puisque AK est connu, alors CK est connu.

en effet, dans la figure ci-contre, $CK= AK-b=\frac{c^2-a^2-b^2}{b}$

Enfin, il fait remarquer que CK étant connu, l'angle KCB est connu

en effet, $\cos(KCB)=\frac{CK}{2a}=\frac{c^2-a^2-b^2}{2ab}$

Et puisque l'angle KCB est connu, il en est de même de l'angle ACB

Ainsi, on retrouve la règle du cosinus : $\cos(\gamma)=\frac{a^2+b^2-c^2}{2ab}$

Ne manipulant pas les mesures algébriques, Nicolas Copernic présente deux cas de figure pour l'angle obtus et l'angle aigu, travaille sur un cercle dont le rayon correspond au plus petit côté, et ne présente pas de formule, mais un algorithme de calcul. Une utilisation analogue de la puissance d'un point par rapport à un cercle pour retrouver la règle du cosinus est faite par Pitiscus^[12]

À l'aide du produit scalaire

En utilisant le calcul vectoriel, plus précisément le produit scalaire, il est possible de retrouver le théorème d'Al-Kashi en quelques lignes^[5] :

$c^2\,$	$=\lVert\overrightarrow{\mathrm{AB}}\lVert^2$
	$= \lVert\overrightarrow{\mathrm{CB}}-\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\lVert\overrightarrow{\mathrm{CB}}\lVert^2-2\cdot\overrightarrow{\mathrm{CB}}\cdot\overrightarrow{\mathrm{CA}}+\lVert\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\mathrm{CB}^2-2\cdot\left\|\mathrm{CB}\right\|\cdot\left\|\mathrm{CA}\right\|\cos\widehat{\mathrm{ACB}}+\mathrm{CA}^2$
	$=a^2+b^2-2ab \cos\gamma\,.$

Généralisation aux géométries non euclidiennes

Pour une surface non euclidienne de courbure K, on note R le rayon de courbure. Il vérifie

$\,R = 1/\sqrt{|K|}$ .

On définit alors les dimensions réduites du triangle :

$\,a = BC/R$ ,

$\,b = AC/R$ ,

$\,c = AB/R$ .

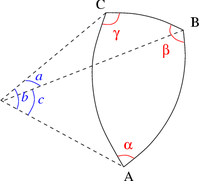
Dans le cas d'un triangle sphérique, a, b et c correspondent à la mesure angulaire des segments de grand arc [BC], [AC] et [AB] (voir Fig. 7).

Géométrie sphérique

Fig. 9 - Triangle sphérique : dimensions réduites a, b et c ; angles α, β et γ.

Dans un triangle sphérique ABC (Fig. 9), le théorème d'Al-Kashi s'écrit^[13]

$\cos c = \cos a \, \cos b + \sin a \, \sin b \, \cos\gamma.$

Lorsque le rayon de courbure est très grand devant les dimensions du triangle, c’est-à-dire lorsque

$\,a <\!\!< 1,\ \,b <\!\!< 1,\ \,c <\!\!< 1,\$

cette expression se simplifie pour donner la version euclidienne du théorème d'Al-Kashi. Pour le montrer, on utilise les développements limités suivants :

$\,\sin a = a + O(a^3),$

$\,\cos a = 1 - a^2/2 + O(a^3).$

Il existe une identité similaire qui relie les trois angles :

$\cos\gamma = - \cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta\,\cos c$

Géométrie hyperbolique

Dans un triangle hyperbolique ABC, le théorème d'Al-Kashi s'écrit^[14]

$\cosh c = \cosh a\,\cosh b - \sinh a\,\sinh b\,\cos\gamma$ .

Lorsque le rayon de courbure devient très grand devant les dimensions du triangle, on retrouve le théorème d'Al-Kashi euclidien à partir des développements limités

$\,\sinh a = a + O(a^3)$ ,

$\,\cosh a = 1 + a^2/2 + O(a^3).$

Généralisation à l'espace euclidien

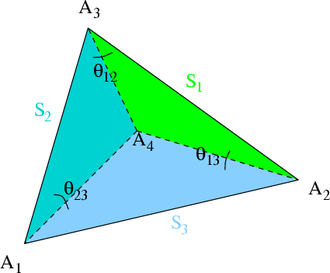
Fig. 10 - Tétraèdre : faces et angles diédraux.

On considère un tétraèdre A₁A₂A₃A₄ de l'espace euclidien. La figure 10 ci-contre présente les notations concernant les sommets, faces et angles dans le tétraèdre :

$S k$ la face opposée au sommet $\mathrm A_k\$ ;
$s k$ la surface de $\mathrm S_k\$ ;
$Δ k$ le plan dans lequel $\mathrm S_k\$ est plongée ;
$θ i j$ l'angle diédral $(Δ i,Δ j)$ .

Alors, surfaces et angles vérifient^[15] :

$s_4^2 = s_1^2+s_2^2+s_3^2 - 2s_1s_2\cos\theta_{12} - 2s_1s_3\cos\theta_{13} - 2s_2s_3\cos\theta_{23}.\,$

Notes et références

↑ Pour une version en ligne de cette proposition (mais en anglais), voir le site de David E. Joyce (en), ou le texte intégral de la traduction de 1632
↑ (en) Yasmeen Mahnaz Faruqi, « Contributions of Islamic scholars to the scientific enterprise », dans International Education Journal, vol. 7, n^o 4, 2006, p. 391-399 (ISSN 1443-1475) [texte intégral (page consultée le 22 décembre 2009)]
↑ Youssef Guergour, Le roi de Saragosse Al-Mutaman Ibn Hud et le théorème de Pythagore : ses sources et ses prolongements, LLULL, vol 28,2005, p 432.
↑ Renée Honvault : Une approche possible de la géométrie plane page 41
↑ ^{a et b} La formule d'Al-Kashi, vue comme application du produit scalaire, est présente dans les programmes de mathématiques de première S de l'enseignement français (voir BO du 31 aout 2000)
↑ Élements d'Euclide selon la traduction d'Henrion (1632) pp 99-104
↑ Selon Youssef Guergour, Le roi de Saragosse Al-Mutaman Ibn Hud et le théorème de Pythagore : ses sources et ses prolongements, LLULL, vol 28,2005, 415-434, la démonstration se trouve dans KASHI (al) (1967): Miftam al-misab [Clé de l'Arithmétique], al-Damardache, A. S. & al-Manfi al-Shikh, M. M. (Edit.), Le Caire, Dar al-Kitab al-cArabi li at-tibaqa wa an-Nashr, pp 130-138
↑ Voir par exemple Nelsen, Roger B. (2000), Proofs without Words II: More Exercises in Visual Thinking, p.9 (publié par la Mathematical Association of America), et plus généralement cet article sur les preuves sans mots (en)
↑ Küstner, Hellwitch, Kästner, Petite encyclopédie des mathématiques, Édition Didier, 1980, ch 11-2, p 265
↑ N. Copernic, De révolutionibus orbium coelestium, Livre I, Chapitre XII, paragraphe VII, p 20 (Lire en ligne)
↑ N. Copernic, De révolutionibus orbium coelestium, Livre I, Chapitre XII, paragraphe VII, p 21 (Lire en ligne)
↑ David Eugene Smith, A source book in mathematics, Volume 1, p 435
↑ Voir l'article trigonométrie sphérique, et pour des démonstrations, par exemple, le "cours" de cartographie de David Madore
↑ Voir l'article géométrie hyperbolique ; pour des démonstrations de ces formules, on pourra par exemple se référer à ce TD de DEA (mais qui utilise des connaissances assez avancées)
↑ (en) Lee, J. R. "The Law of Cosines in a Tetrahedron." J. Korea Soc. Math. Ed. Ser. B: Pure Appl. Math. 4, 1-6, 1997.

Voir aussi

Articles connexes

Trigonométrie	Géométrie du triangle	Mathématiciens
triangulation	théorème de Pythagore	Euclide
trigonométrie sphérique	Livre II des Éléments d'Euclide	al-Battani
fonction trigonométrique	loi des sinus	Ghiyath al-Kashi
	loi des tangentes	François Viète

Liens externes

Ces liens ont servi de sources de l'article

Les Éléments, tome II, Euclide, sur la Bibliothèque nationale française en ligne.
Law of cosines, sur le site Math World (en anglais)

Bibliographie

N. Éfimov,Géométrie Supérieure, Moscou, Éditions MIR, 1981
Collectif, Petite Encyclopédie des Mathématiques, Paris, Éditions K. Pagoulatos, 1980
Antoine Arnauld, Nouveaux éléments de géométrie, Paris, Charles Savreux, 1667,p295-296 (Sixième théorème)
Amiot, Eléments de géométrie, Paris, Delagrave, 14e édition, 1870, p109-111
Cirodde, Leçons de géométrie, Paris, Hachette, 3e édition, 1858, p111-112 (théorème XI)

Cet article est reconnu comme « article de qualité » depuis sa version du 14 février 2005 (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu.

Catégories :

Géométrie du triangle
Mathématiques élémentaires
Trigonométrie
Théorème de géométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'Al-Kashi de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme d'Al-Kashi — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Théorème d'Al-kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème d'Al Kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème d'al-kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème de Pythagore généralisé — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Théorème du cosinus — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Theoreme de Pythagore — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de l'hypoténuse — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de pythagore — Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit)… … Wikipédia en Français
Theoreme de Morley — Théorème de Morley Le théorème de Morley, découvert par Frank Morley en 1898, est un théorème de géométrie plane. Il s énonce comme suit : « Les intersections des trissectrices des angles d un triangle forment un triangle… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème d'Al-Kashi

Sommaire

Histoire

Le théorème et ses applications