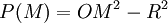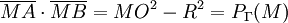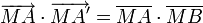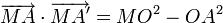Puissance d'un point par rapport a un cercle

Puissance d'un point par rapport a un cercle

Puissance d'un point par rapport à un cercle

En géométrie euclidienne du plan, la puissance d'un point M par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de M par rapport à ce cercle. Elle peut être définie comme

P(M)=OM^2-R^2\,

Sommaire

Propriété fondamentale et définition

Si M est un point et Γ est un cercle de centre O et de rayon R, alors, pour toute droite passant par M et rencontrant le cercle en A et B, on a :
MA × MB = |MO² - R²|. Cette valeur ne dépend pas de la droite choisie, mais seulement de la position de M par rapport au cercle.

On peut remarquer que :

  • si M est à l’extérieur du cercle, MA × MB = MO² - R²
  • si M est à l’intérieur du cercle , OM² - R² = - MA × MB . Ce produit correspond au produit des mesures algébriques de MA et MB

Théorème et définition — Soient M un point, Γ un cercle de centre O et de rayon R et (d) une droite passant par M et rencontrant le cercle en A et B. On appelle alors puissance du point M par rapport au cercle Γ le produit des mesures algébriques de MA et MB. Ce produit est indépendant de la droite choisie et vaut toujours :

\overline{MA}\cdot\overline{MB} = MO^2-R^2 = P_\Gamma(M)\,
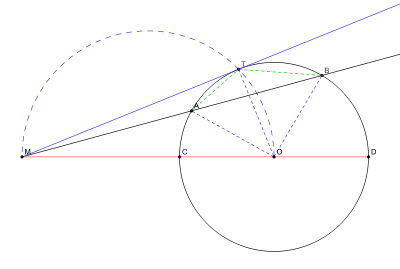
Puissance point ext.svg

Lorsque le point M est à l'extérieur du cercle, il est possible de mener des tangentes au cercle. En appelant T le point de contact du cercle avec une de ces tangentes, la puissance de M est PΓ(M) = MT2 (théorème de Pythagore).


Démonstrations

Cas où M est à l'extérieur du cercle On utilise ici la propriétés des angles inscrits et les triangles semblables

L'angle inscrit 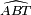\scriptstyle \widehat {ABT} interceptant l'arc AT est égal à l'angle 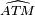\scriptstyle\widehat {ATM} de la corde [AT] et de la tangente [MT). Les triangles MBT et MTA ont cet angle égal et l'angle 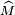\scriptstyle \widehat M en commun : ils sont donc semblables.
Des rapports de similitude égaux 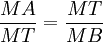\frac {MA} {MT} = \frac {MT} {MB} on déduit, avec l'égalité des produits des extrêmes et des moyens, que MA × MB = MT2.
l résulte que le produit MA × MB ne dépend pas de la sécante, mais seulement du point M.
En particulier pour la sécante (MO) la puissance du point M est aussi MC × MD = (MO - OC) × (MO + OD) = MO2 - OD2 = MO2 - R2.

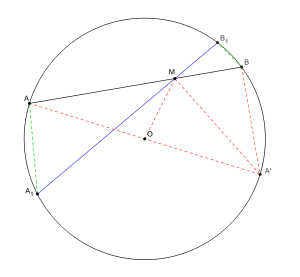
Cas où M est intérieur au cercle Une démonstration analogue peut être faite pour démontrer que le produit est indépendant de la sécante. Il suffit de prouver que les triangles MAA1 et MB1B sont semblables. Mais on peut aussi présenter une démonstration faisant appel au produit scalaire ce qui illustre que de nombreux outils différents permettent de démontrer une même propriété.

Puissance point int.svg
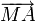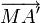Dans la figure ci-jointe, le point A' est le symétrique du point A par rapport à O. Le calcul du produit scalaire des vecteurs \scriptstyle \overrightarrow{MA} et \scriptstyle \overrightarrow{MA'} sous deux formes différentes conduit à l'égalité cherchée.
En projetant orthogonalement A' sur (MA) en B
\overrightarrow{MA}\cdot \overrightarrow{MA'} = \overline{MA}\cdot \overline{MB}
En utilisant un théorème de la médiane dans le triangle (MAA')
\overrightarrow{MA}\cdot \overrightarrow{MA'} = MO^2-OA^2

L'égalité MA × MB = MT2 est suffisante pour affirmer que la droite (MT) est tangente au cercle.

La puissance d'un point permet de vérifier que quatre points sont cocycliques : en effet, si A, B, C, D sont quatre points tels que(AB) et (CD) se coupent en M et si 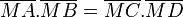\overline{MA} . \overline{MB} = \overline{MC} . \overline{MD} (ce sont les mesures algébriques) alors les quatre points sont cocycliques.

Axe radical de deux cercles

L'axe radical de deux cercles, de centres distincts, est l'ensemble des points ayant même puissance par rapport à ces deux cercles.

Axe radical.svg

On considère deux cercles c(O, R) et c'(O', R') avec O et O' distincts. L'ensemble des points M de mêmes puissances par rapport aux deux cercles vérifie :

pc(M) = MO2 - R2 = pc'(M) = MO'2 - R'2, soit MO2 - MO'2 = R2 - R'2.

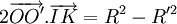Soit I le milieu de [OO'] et K la projection de M sur (OO'). D'après le troisième théorème de la médiane dans le triangle MOO', on a : 2\overrightarrow{OO'}.\overrightarrow{IK} = R^2 - R'^2.
Tous ces points M ont le même projeté orthogonal sur la droite (OO’), et la formule obtenue ci-dessus permet de construire ce projeté K.
L'axe radical est donc la droite perpendiculaire à ligne des centres passant par K.

Si les cercles sont sécants, l'axe radical est la droite joignant les points d'intersection.

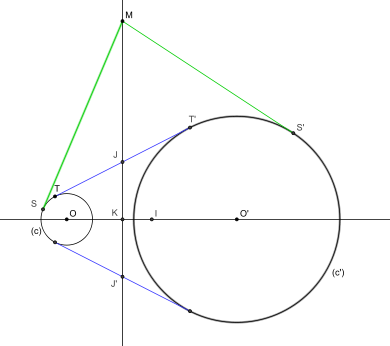
L'axe radical (éventuellement en dehors du segment intérieur aux deux cercles) est aussi l'ensemble des points desquels on peut mener, aux deux cercles, des segments tangents de même longueur (MS = MS' dans la figure ci-contre).

En particulier si les cercles sont extérieurs et admettent une tangente commune (TT'), le milieu J de [TT'] appartient à l'axe radical. Cette propriété permet de construire l'axe radical.

Centre radical de trois cercles

Les axes radicaux de trois cercles de centres non alignés concourent en un point appelé centre radical des trois cercles.

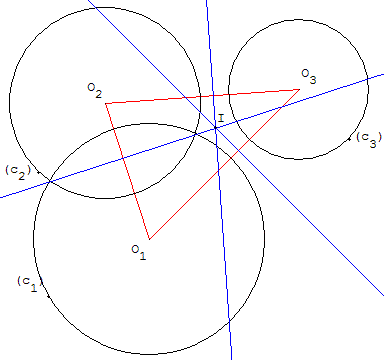
Centre radical.gif

Voir : cercle orthogonal à trois cercles

Voir aussi

Articles connexes

Liens externes

"Avec GéoPlan" : la géométrie du cercle

"Avec Cabri" : puissance d'un point par rapport à un cercle

  • Portail de la géométrie Portail de la géométrie

Ce document provient de « Puissance d%27un point par rapport %C3%A0 un cercle ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Puissance d'un point par rapport a un cercle de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Puissance d'un point par rapport à un cercle — En géométrie euclidienne du plan, la puissance d un point M par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de M par rapport à ce cercle. Elle peut être définie comme Sommaire 1 Propriété fondamentale et… …   Wikipédia en Français

  • puissance — [ pɥisɑ̃s ] n. f. • 1150; de puissant I ♦ (Sens faible) 1 ♦ Vx Puissance de... : moyen ou droit grâce auquel on peut (faire qqch.). ⇒ capacité. « La puissance de bien juger [...] est égale en tous les hommes » (Descartes). 2 ♦ Mod. Philos.… …   Encyclopédie Universelle

  • Cercle — Pour les articles homonymes, voir cercle (homonymie). Un cercle est une courbe plane fermée constituée des points situés à égale distance d un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Celui ci étant infiniment… …   Wikipédia en Français

  • point — 1. point [ pwɛ̃ ] n. m. • 1175 « endroit, moment »; lat. punctum « piqûre », de pungere → poindre I ♦ A ♦ Portion de l espace déterminée avec précision. 1 ♦ Endroit, lieu. En divers, en plusieurs points. « il relevait la tête et fixait son regard …   Encyclopédie Universelle

  • Puissance — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Puissance », sur le Wiktionnaire (dictionnaire universel) Le mot puissance est employé dans plusieurs… …   Wikipédia en Français

  • Arc de cercle — Cercle Pour les articles homonymes, voir cercle (homonymie). Un cercle est une courbe plane fermée constituée des points situés à égale distance d un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Celui ci étant… …   Wikipédia en Français

  • Équation d'un cercle — Cercle Pour les articles homonymes, voir cercle (homonymie). Un cercle est une courbe plane fermée constituée des points situés à égale distance d un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Celui ci étant… …   Wikipédia en Français

  • point — 1. (poin ; le t se lie : un poin t important ; au pluriel, l s se lie : des points z importants) s. m. 1°   Douleur qui point, qui pique. 2°   Piqûre que l on fait dans l étoffe avec une aiguille enfilée d un fil. 3°   Nom donné à certains… …   Dictionnaire de la Langue Française d'Émile Littré

  • Cercle Bruges KSV —  Ne pas confondre avec le Club Bruges KV, un autre club de la ville de Bruges avec lequel le Cercle entretient une rivalité depuis sa création. Infobox club sportif Cercle Brugge K.S.V …   Wikipédia en Français

  • Puissance du libéralisme — Libéralisme Pour les articles homonymes, voir Libéralisme (homonymie).  Ne doit pas être confondu avec Libertaire ou Libertarianisme. Le libéralisme est un courant de pensée de philosophie politique, né d une opposition à l absolutisme et au …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”