Theoreme du moment cinetique

Theoreme du moment cinetique

Théorème du moment cinétique

En mécanique classique, le théorème du moment cinétique est un résultat fondamental, corollaire utile des lois du mouvement de Newton. Il se révèle très pratique dans l'étude des problèmes à deux corps et en mécanique du solide.

Le théorème du moment cinétique est notamment utilisé dans l'étude des mouvements à force centrale, car celles-ci ont une contribution nulle au moment cinétique pris en un point particulier, ce qui simplifie parfois grandement l'analyse. C'est ainsi qu'il est utilisé pour démontrer la seconde loi de Kepler décrivant les mouvements des planètes autour du Soleil. D'un point de vue plus fondamental, le théorème du moment cinétique est une" des applications directes d'un théorème mathématique appelé théorème de Noether.

Le théorème du moment cinétique relie deux quantités physiques : le moment cinétique et l'ensemble des moments des forces s'exerçant sur un objet donné..

Sommaire

Mécanique du point

Énoncé

On se place dans un référentiel galiléen[1]. On considère un point fixe, de rayon vecteur r'. Soit un point matériel repéré par le rayon vecteur r, de masse m, de vitesse v et de quantité de mouvement p. Le moment cinétique du point matériel par rapport au point r' est défini par :

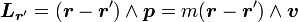\boldsymbol L_{\boldsymbol r'} = (\boldsymbol r - \boldsymbol r') \wedge \boldsymbol p = m (\boldsymbol r - \boldsymbol r') \wedge \boldsymbol v,

où le symbole ∧ représente le produit vectoriel usuel. En notant F l'ensemble des forces s'appliquant sur le point matériel, on définit le moment de F en r' par :

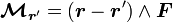\boldsymbol {\mathcal M}_{\boldsymbol r'} = (\boldsymbol r - \boldsymbol r') \wedge \boldsymbol F.

Le théorème du moment cinétique énonce que :

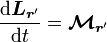\frac{{\rm d}\boldsymbol L_{\boldsymbol r'}}{{\rm d} t} = \boldsymbol {\mathcal M}_{\boldsymbol r'}.

Démonstration

En effectuant l'opération de dérivation sur le moment cinétique, on a :

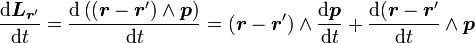\frac{\mathrm d \boldsymbol L_{\boldsymbol r'}}{\mathrm dt} = \frac{\mathrm d \left( (\boldsymbol r - \boldsymbol r') \wedge \boldsymbol p \right)}{\mathrm dt} = (\boldsymbol r - \boldsymbol r') \wedge \frac{\mathrm d \boldsymbol p }{\mathrm dt} + \frac{\mathrm d (\boldsymbol r - \boldsymbol r' }{\mathrm dt} \wedge \boldsymbol p.

D'après le principe fondamental de la dynamique, la dérivée de la quantité de mouvement est égale à la somme des forces. D'autre part, la quantité de mouvement est colinéaire à la vitesse, donc le second produit vectoriel est nul. On a ainsi

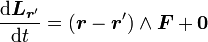\frac{\mathrm d \boldsymbol L_{\boldsymbol r'}}{\mathrm dt} = (\boldsymbol r - \boldsymbol r') \wedge \boldsymbol F + \boldsymbol 0,

soit

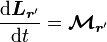\frac{\mathrm d \boldsymbol L_{\boldsymbol r'}}{\mathrm dt} = \boldsymbol{\mathcal M}_{\boldsymbol r'}.

Utilisation : équation du pendule simple

Article détaillé : Pendule simple.
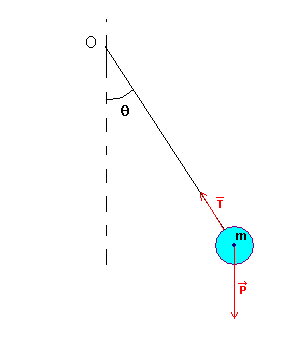Le cas du pendule simple est facilement traité par le théorème du moment cinétique.

On considère un pendule simple, constitué d'une masse m, repéré par sa position en coordonnées polaires (r, θ) et accrochée par un fil inextensible parfait de longueur l à un point fixe O correspondant à l'origine du système de coordonnées. Le pendule est supposé soumis uniquement au champ de pesanteur, considéré uniforme et égal à g, de direction et de module constant. Le fil forme un angle θ avec la verticale.

Le moment des forces autre que le poids (réaction au niveau de la liaison pivot et force de tension du fil) pris au point d'attache du fil au support O est nul. Le moment exercé par le poids à ce point d'attache est :

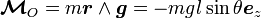\boldsymbol {\mathcal M}_{O} = m \boldsymbol r \wedge \boldsymbol g = - mgl \sin \theta \boldsymbol e_z.

Le moment cinétique de la masse en O s'écrit :

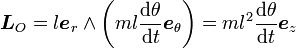\boldsymbol L_O = l \boldsymbol e_r \wedge \left(m l \frac{\mathrm d \theta}{\mathrm dt} \boldsymbol e_\theta \right) = ml^2 \frac{\mathrm d \theta}{\mathrm dt} \boldsymbol e_z.

En dérivant cette dernière relation, et en projetant le long de l'axe ez, on a, d'après le théorème du moment cinétique :

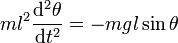ml^2 \frac{\mathrm d^2 \theta}{\mathrm dt^2} = - mgl \sin \theta,

ou bien, la dérivée par rapport au temps par un point :

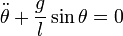\ddot{\theta} + \frac{g}{l} \sin \theta = 0.

C'est la formule bien connue de l'équation du pendule plan simple.

Note

  1. ↑ L'utilisation d'un référentiel non-galiléen a pour effet la violation du principe fondamental de la dynamique, à moins qu'on y introduise les forces d'inertie. Le théorème du moment cinétique reste valable dans un tel référentiel si on prend en compte l'effet de ces deux forces virtuelles.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Th%C3%A9or%C3%A8me du moment cin%C3%A9tique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme du moment cinetique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Théorème du moment cinétique — En mécanique classique, le théorème du moment cinétique est un résultat fondamental, corollaire utile des lois du mouvement de Newton. Il se révèle très pratique dans l étude des problèmes à deux corps et en mécanique du solide. Le théorème du… …   Wikipédia en Français

  • Moment cinetique — Moment angulaire Pour les articles homonymes, voir Moment. Un gyroscope tournant sur un clou En physique, le moment angulaire ou mom …   Wikipédia en Français

  • Moment cinétique — Moment angulaire Pour les articles homonymes, voir Moment. Un gyroscope tournant sur un clou En physique, le moment angulaire ou mom …   Wikipédia en Français

  • Moment Angulaire — Pour les articles homonymes, voir Moment. Un gyroscope tournant sur un clou En physique, le moment angulaire ou mom …   Wikipédia en Français

  • Moment angulaire — Pour les articles homonymes, voir Moment. Un gyroscope tournant sur un clou En physique, le moment angulaire ou moment cinétique est la grandeur physique qui joue dans le ca …   Wikipédia en Français

  • CINÉTIQUE — La cinétique, théorie partielle de la mécanique, fait appel aux notions de longueur, de temps et de masse. Elle est le prolongement de la cinématique, puisque son élaboration ne demande que l’introduction d’une nouvelle notion: celle de masse. On …   Encyclopédie Universelle

  • Moment D'inertie — Pour les articles homonymes, voir Moment. Lequel de ces mouvements est le plus difficile ? Le moment d inertie quantifie la résistance d un …   Wikipédia en Français

  • Théorème de Huygens — Moment d inertie Pour les articles homonymes, voir Moment. Lequel de ces mouvements est le plus difficile ? Le moment d inertie quantifie la résistance d un …   Wikipédia en Français

  • Theoreme de Siacci — Théorème de Siacci Le théorème de Siacci est un théorème de cinématique qui s applique aux courbes planes paramétrées par la distance à l origine et la distance de l origine à la podaire. Il peut servir utilement dans le cas de force centrale.… …   Wikipédia en Français

  • Théorème de Sciacci — Théorème de Siacci Le théorème de Siacci est un théorème de cinématique qui s applique aux courbes planes paramétrées par la distance à l origine et la distance de l origine à la podaire. Il peut servir utilement dans le cas de force centrale.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”