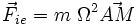Forces D'inertie

Forces D'inertie

Force d'inertie

Une force d'inertie, ou inertielle, ou force fictive, est une force apparente qui agit sur les masses lorsqu'elles sont observées à partir d'un référentiel non inertiel, autrement dit d'un point de vue en mouvement accéléré ou en rotation. Une telle force n'est pas le résultat d'une interaction physique, mais plutôt de l'inertie s'opposant à l'accélération du référentiel lui-même.

Les principales forces fictives sont la force centrifuge et la force de Coriolis.

Sommaire

Exposé

La mécanique classique fait intervenir les lois de Newton, et celles-ci ne sont valables que dans un référentiel galiléen.

Si l'on se place dans un référentiel non inertiel ayant un mouvement accéléré par rapport à un référentiel galiléen (par exemple accélération linéaire ou bien rotation), les lois de Newton ne peuvent plus s'écrire, sauf en ajoutant des forces fictives: les forces d'inertie.

Pour l'observateur extérieur (situé dans le référentiel galiléen), il n'y a pas de force d'inertie. Il n'y a qu'un effet de l'inertie, c'est-à-dire que les phénomènes observés proviennent du fait qu'il faut fournir un effort pour modifier le mouvement initial d'un objet (« tout corps jeté dans l'espace tend à reproduire son mouvement à l'infini ».

Par exemple, une personne est dans une voiture, et cette voiture démarre brusquement. La personne sent une force qui la plaque contre le dossier, elle subit la force d'inertie. Considérons maintenant un observateur extérieur : il verra juste un effet de l'inertie : lorsque la voiture démarre, la personne assise est immobile et est donc « rattrapée » par son dossier, et c'est la pression exercée par le dossier sur la personne qui va mettre celle-ci en mouvement, qui va la pousser et faire qu'elle se déplace à la même vitesse que le reste de la voiture.

Expressions

Soit (R) un référentiel galiléen centré en 0, et (R') un référentiel non galiléen centré en A, dont la rotation autour de (R) est donnée par le vecteur 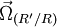\vec{\Omega}_{(R'/R)}. Soit un point M mobile de masse m subissant des forces de résultante \vec{F}.

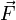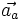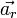Alors, d'après la loi de composition des mouvements, en notant \vec{a_a} l'accélération de M dans (R), \vec{a_r} l'accélération de M dans (R'), 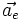\vec{a_e} l'accélération d'entraînement et enfin 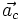\vec{a_c} l'accélération de Coriolis, on a :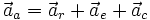

\vec{a}_a=\vec{a}_r+\vec{a}_e+\vec{a}_c

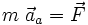
Or, d'après le principe fondamental de la dynamique, on a : m\ \vec{a}_a=\vec{F}

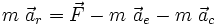
D'où, dans (R'): m\ \vec{a}_r=\vec{F}-m\ \vec{a}_e-m\ \vec{a}_c

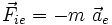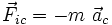En définissant les forces d'inertie \vec{F}_{ie}=-m\ \vec{a}_e et \vec{F}_{ic}=-m\ \vec{a}_c, on peut alors écrire le PFD dans le référentiel (R') non galiléen :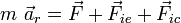

m\ \vec{a}_r=\vec{F}+\vec{F}_{ie}+\vec{F}_{ic}

La force 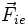\vec{F}_{ie} est appelée force d'inertie d'entrainement, et son expression développée est :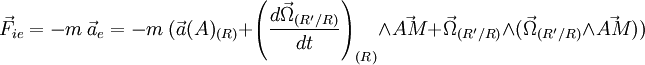

\vec{F}_{ie}=-m\ \vec{a}_e=-m\ ( \vec{a}(A)_{(R)}+\left ( \frac{d\vec{\Omega}_{(R'/R)}}{dt} \right )_{(R)}\wedge \vec{AM}+\vec{\Omega}_{(R'/R)}\wedge(\vec{\Omega}_{(R'/R)}\wedge\vec{AM}))

La force 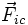\vec{F}_{ic} est appelée force d'inertie de Coriolis, et son expression développée est :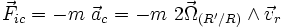

\vec{F}_{ic}=-m\ \vec{a}_c=-m\ 2\vec{\Omega}_{(R'/R)}\wedge \vec{v}_r

Quelques cas d'application simples

Référentiel en accélération constante dans un référentiel galiléen

Supposons que (R') subisse une accélération constante 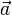\vec{a} dans (R). (R') est donc animé d'un mouvement linéaire uniformément accéléré dans R.

Dans R, il faut ajouter la force d'inertie d'entrainement 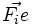\vec{F_ie} qui vaut alors simplement :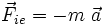 \vec{F}_{ie} = -m \ \vec{a}

C'est ce qui se passe par exemple dans une voiture en ligne droite : la force d'inertie s'oppose à l'accélération de la voiture.

Référentiel en rotation uniforme

Dans un manège tournant à la vitesse angulaire Ω, nous avons tendance à nous éloigner du centre de rotation noté A: cela est du à la force d'inertie d'entrainement qui vaut alors :

\vec{F}_{ie}=m\ \Omega^2\vec{AM}

Cette force est encore appelée force centrifuge car elle a tendance à éloigner un objet de l'axe de rotation.

« Vraies » ou « fausses » forces ?

Une force est un modèle destiné à représenter une interaction ; quelle que soit la nature de l'interaction, celle-ci est représentée par un vecteur ayant un point d'application, une direction, un sens et une intensité (en newton). C'est le cas des interactions de contact (pression, frottement) ou à distance (poids, force électrostatique, force de Lorentz).

En ce sens, les forces d'inertie ne résultent pas d'une interaction (c'est-à-dire de l'action d'un l'objet sur un autre) mais juste du choix du référentiel, ce ne sont donc pas à proprement parler des forces mais un simple artifice de calcul.

Cependant, si l'on définit une force par son effet, c'est-à-dire par l'accélération ou la déformation qu'elle produit, alors les forces d'inertie sont bien des forces.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Force d%27inertie ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Forces D'inertie de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Forces d'inertie — Force d inertie Une force d inertie, ou inertielle, ou force fictive, est une force apparente qui agit sur les masses lorsqu elles sont observées à partir d un référentiel non inertiel, autrement dit d un point de vue en mouvement accéléré ou en… …   Wikipédia en Français

  • inertie — [ inɛrsi ] n. f. • inhertie « atonie », h. v. 1370; lat. inertia ♦ État de ce qui est inerte. 1 ♦ Résistance des objets pesants au mouvement qui leur est imposé. L inertie de la matière. Centre d inertie. ⇒ gravité; barycentre. Force d inertie… …   Encyclopédie Universelle

  • Forces de marée — Force de marée La comète Shoemaker Levy 9 en 1994 après avoir été brisée par les forces de marée de Jupiter au cours d un passage précédent, en 1992. La force de marée est une conséquence de la non uniformité de la force de gravitation exercée… …   Wikipédia en Français

  • Forces de gravitation — Gravitation « Gravitation » redirige ici. Pour les autres significations, voir Gravitation (homonymie). La gravitation est le phénomène d interaction physique qui cause l attraction réciproque des corps massifs entre eux, sous l effet… …   Wikipédia en Français

  • Inertie — Pour les articles homonymes, voir Inertie (homonymie). En physique, et dans un référentiel galiléen (dit inertiel), l inertie d un corps est sa résistance à une variation de vitesse. L inertie est fonction de la masse du corps : plus celle… …   Wikipédia en Français

  • Centre d'inertie — Le centre d inertie d un objet, ou centre de masse, est le point de l espace où l on applique les effets d inertie, c est à dire le vecteur variation de quantité de mouvement . Si la masse du système est constante, ce que nous supposerons pour… …   Wikipédia en Français

  • Force d'inertie — Une force d inertie, ou inertielle, ou force fictive, est une force apparente qui agit sur les masses lorsqu elles sont observées à partir d un référentiel non inertiel, autrement dit d un point de vue en mouvement accéléré ou en rotation. Une… …   Wikipédia en Français

  • Échauffement dû aux forces de marées — Force de marée La comète Shoemaker Levy 9 en 1994 après avoir été brisée par les forces de marée de Jupiter au cours d un passage précédent, en 1992. La force de marée est une conséquence de la non uniformité de la force de gravitation exercée… …   Wikipédia en Français

  • Référentiel d'inertie — Référentiel galiléen En physique, un référentiel galiléen, ou inertiel, est un référentiel dans lequel un objet isolé (sur lequel ne s’exerce aucune force ou sur lequel la résultante des forces est nulle) est soit immobile, soit en mouvement de… …   Wikipédia en Français

  • Principe d’inertie — Lois du mouvement de Newton Les deux premières lois de Newton en latin dans l édition originale du Principia Mathematica de 1687. Les lois du mouvement de Newton sont en fait des principes à la base de la grande théorie de Newton concernant le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”