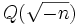Nombre d'Heegner
- Nombre d'Heegner
-
Nombre de Heegner
En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique
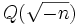
possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d'entiers possède une factorisation unique. Voir le théorème de Stark-Heegner pour la démonstration qui indique que de tels n qui sont sans carré sont en nombre fini.
Les nombres de Heegner sont: 1, 2, 3, 7, 11, 19, 43, 67 et 163.
Ce dernier a l'étonnante propriété de faire de 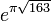 un nombre presque entier, puisqu'il vaut : 262537412640768743,999999999999250072...
un nombre presque entier, puisqu'il vaut : 262537412640768743,999999999999250072...
Anecdote
En 1975, Martin Gardner proposa dans la revue Scientific American un poisson d'avril, dans lequel il prétendait que 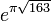 était un entier puisque les calculatrices de l'époque n'avaient pas une grande précision.
était un entier puisque les calculatrices de l'époque n'avaient pas une grande précision.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Propriété numérique | Entier quadratique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Nombre d'Heegner de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Nombre De Heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… … Wikipédia en Français
Nombre de heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… … Wikipédia en Français
Nombre de Heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… … Wikipédia en Français
Nombre chanceux d'Euler — Ne doit pas être confondu avec nombre chanceux. En mathématiques, un nombre chanceux d Euler est un entier A > 1 tel que : PA(n) = n2 + n + A est un nombre premier pour tout n = 0,1,...,A − 2[1 … Wikipédia en Français
Nombre de classes — Groupe des classes d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des… … Wikipédia en Français
Nombre presque entier — En mathématiques récréatives, un nombre presque entier est un nombre irrationnel qui est de façon surprenante très proche d un entier. Sommaire 1 Quelques cas 1.1 Puissances du nombre d or 1.2 Constante de Ramanujan … Wikipédia en Français
Problème du nombre de classes pour les corps quadratiques imaginaires — En mathématiques, le problème du nombre de classes de Gauss pour les corps quadratiques imaginaires, au sens usuel, est de fournir pour chaque entier n ≥ 1, la liste complète des corps quadratiques imaginaires dont le nombre de classes vaut n. C… … Wikipédia en Français
Probleme du nombre de classes pour les corps quadratiques imaginaires — Problème du nombre de classes pour les corps quadratiques imaginaires En mathématiques, le problème du nombre de classes de Gauss pour les corps quadratiques imaginaires, comme il est généralement compris, est de fournir pour chaque une liste… … Wikipédia en Français
11 (nombre) — « Onze » redirige ici. Cet article concerne le nombre 11. Pour l année, voir 11. 11 … Wikipédia en Français
19 (nombre) — « Dix neuf » redirige ici. Cet article concerne le nombre 19. Pour l année, voir 19. 19 … Wikipédia en Français
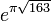 un nombre presque entier, puisqu'il vaut : 262537412640768743,999999999999250072...
un nombre presque entier, puisqu'il vaut : 262537412640768743,999999999999250072...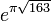 était un entier puisque les calculatrices de l'époque n'avaient pas une grande précision.
était un entier puisque les calculatrices de l'époque n'avaient pas une grande précision.