Probleme du nombre de classes pour les corps quadratiques imaginaires

Probleme du nombre de classes pour les corps quadratiques imaginaires

Problème du nombre de classes pour les corps quadratiques imaginaires

En mathématiques, le problème du nombre de classes de Gauss pour les corps quadratiques imaginaires, comme il est généralement compris, est de fournir pour chaque 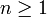n \ge 1\, une liste complète de corps quadratiques imaginaires avec un nombre de classes n. C'est une question de calcul. Le résultat de base qui fut donna l'assurance qu'une telle liste serait finie fut, dans la forme démontrée autour de 1930, permit même en principe de la calculer. Voir Résultats effectifs en théorie des nombres.

Dans les développements ultérieurs, le cas n = 1 fut en premier développé par Kurt Heegner, en utilisant les formes modulaires et les équations modulaires. Ce travail ne fut pas accepté initialement; la situation fut clarifiée seulement après le travail ultérieur d'Harold Stark, et le travail d'Heegner fut compris. Voir le théorème de Stark-Heegner, les nombre d'Heegner. Le cas n = 2 fut abordé peu après, au moins en principe, en application du travail d'Alan Baker.

Le cas général attendit la découverte de Dorian Goldfeld, que le problème du nombre de classes puisse être relié aux fonctions L des courbes elliptiques. Ceci réduisit la question, en principe, à une détermination efficiente, pour qu'on établisse l'existence d'un zéro multiple d'une telle fonction L. Ceci pouvait être fait sur la base du théorème de Gross-Zagier ultérieur. Ainsi, à ce point, on peut préciser un calcul fini, le résultat de ce qui serait une liste complète pour un nombre de classes donné. En fait, en pratique, de telles listes qui sont probablement complètes peuvent être faites par des méthodes relativement simples; dont l'issue est certaine. Les cas plus élevés que n = 100 ont été réalisés maintenant (2004) [1].

Le cas contrastant des corps quadratiques réels est très différent, et est beaucoup moins connu. Ceci car ce que l'on entre dans la formule analytique pour la classe de nombres n'est pas h, le nombre de classes, mais 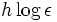h \log \epsilon\,, où \epsilon\, est une unité fondamentale. Ce facteur supplémentaire est difficile à contrôler. Il peut très bien être le cas où le nombre de classes 1 pour les corps quadratiques apparaît infiniment souvent.

Ce document provient de « Probl%C3%A8me du nombre de classes pour les corps quadratiques imaginaires ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Probleme du nombre de classes pour les corps quadratiques imaginaires de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Problème du nombre de classes pour les corps quadratiques imaginaires — En mathématiques, le problème du nombre de classes de Gauss pour les corps quadratiques imaginaires, au sens usuel, est de fournir pour chaque entier n ≥ 1, la liste complète des corps quadratiques imaginaires dont le nombre de classes vaut n. C… …   Wikipédia en Français

  • QUADRATIQUES (FORMES) — La notion de forme quadratique intervient dans toutes les parties des mathématiques. Elle est à la base de la géométrie euclidienne et de la mécanique classique (énergie cinétique), et aussi de la notion d’espace de Hilbert, de la théorie… …   Encyclopédie Universelle

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e …   Wikipédia en Français

  • Theoreme de Stark-Heegner — Théorème de Stark Heegner Le théorème de Stark Heegner est un théorème de la théorie des nombres qui indique précisément quel corps de nombres quadratique imaginaire admet une décomposition en facteurs premiers unique dans leur anneau d entiers.… …   Wikipédia en Français

  • Théorème de stark-heegner — Le théorème de Stark Heegner est un théorème de la théorie des nombres qui indique précisément quel corps de nombres quadratique imaginaire admet une décomposition en facteurs premiers unique dans leur anneau d entiers. Il résout un cas… …   Wikipédia en Français

  • Théorème de Fermat sur les sommes de deux carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • NOMBRES (THÉORIE DES) - Nombres algébriques — Les mathématiciens grecs avaient découvert que certains rapports de grandeurs ne sont pas rationnels, c’est à dire qu’ils ne sont pas égaux au rapport de deux entiers: il en est ainsi du rapport de la diagonale d’un carré à son côté, puisque… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”