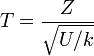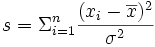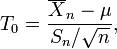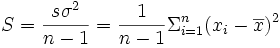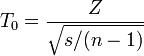- Test de Student
-
Loi de Student
Loi de Student Densité de probabilité / Fonction de masse
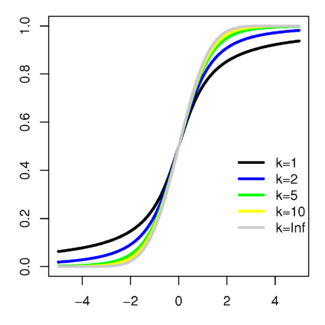
Fonction de répartition
Paramètres k ≥ 1 degrés de liberté, Support ![x \in ]-\infty; +\infty[\,](/pictures/frwiki/97/af0a1a7b903258416f3ac7ff74924900.png)
Densité de probabilité (fonction de masse) 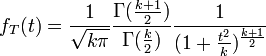
Fonction de répartition 1-γ = ƒ(tγk ), voir tableau en fin d'article Espérance si k = 1 : non définie si k > 1 : 0
Médiane (centre) 0 Mode 0 Variance si k ≤ 2 : 
si k > 2 :
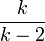
Asymétrie (statistique) 0 pour k > 3 Kurtosis (non-normalisé) Entropie Fonction génératrice des moments Fonction caractéristique La loi de Student est une loi de probabilité, faisant intervenir le quotient entre une variable suivant une loi normale centrée réduite et la racine carrée d'une variable distribuée suivant la loi du χ².
Soit Z une variable aléatoire de loi normale centrée et réduite et soit U une variable indépendante de Z et distribuée suivant la loi du χ² à k degrés de liberté. Par définition la variable
suit une loi de Student à k degrés de liberté.
La densité de
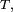 notée
notée 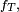 est donnée par :
est donnée par :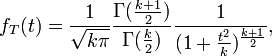 pour k ≥ 1.
pour k ≥ 1.
où Γ est la fonction Gamma d'Euler.
La densité
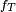 associée à la variable
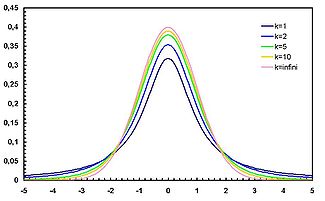
associée à la variable 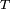 est symétrique, centrée sur 0, en forme de cloche.
est symétrique, centrée sur 0, en forme de cloche.Son espérance ne peut pas être définie pour k = 1, et est nulle pour k > 1.
Sa variance est infinie pour k ≤ 2 et vaut
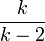 pour k > 2.
pour k > 2.Sommaire
Histoire
Le calcul de la distribution de Student a été publié en 1908 par William Gosset pendant qu'il travaillait à la brasserie Guinness à Dublin. Il lui était interdit de publier sous son propre nom, c'est pour cette raison qu'il publia sous le pseudonyme de Student. Le test-t et de la théorie est devenue célèbre grâce aux travaux de Ronald Fisher, qui a qualifié cette distribution de « distribution de Student ».
Comportement limite
Lorsque k est grand, la loi de Student peut être approchée par la loi normale centrée réduite.
Application : intervalle de confiance associé à l’espérance d’une variable de loi normale de variance inconnue
Ce chapitre présente une méthode pour déterminer l'intervalle de confiance de l'estimateur de l’espérance μ d’une loi normale dont la variance σ² est inconnue.
Théorème — L'intervalle de confiance de μ au seuil de confiance α est donné par:
![\left[\,\overline{x} - t_{(1 - \alpha)/2}^{n-1}\sqrt{\frac{S}{n}\,}, \overline{x} + t_{(1 - \alpha)/2}^{n-1}\sqrt{\frac{S}{n}}\,\right]](/pictures/frwiki/100/dd353edec4bfa9392cae238affce7f77.png) ,
,avec
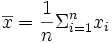 , l'estimateur de l'espérance.
, l'estimateur de l'espérance.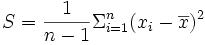 , l'estimateur non-biaisé de la variance.
, l'estimateur non-biaisé de la variance.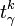 le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (dont la définition exacte est donnée ci-dessus).
le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (dont la définition exacte est donnée ci-dessus).
DémonstrationSoient x1, …, x n n variables indépendantes distribuées suivant une même loi normale d’espérance μ (à déterminer) et de variance σ² (inconnue).
Afin de parvenir au résultat, il est nécessaire d’introduire les variables
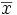 et s.
et s.Soit
La variable
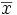 suit la loi normale d’espérance μ et de variance
suit la loi normale d’espérance μ et de variance 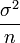 .
.Soit
La variable aléatoire s suit la loi du χ² à n - 1 degrés de liberté.
Remarque : ce résultat utile se démontre à partir de la propriété définissant la loi du χ² en tant que somme des carrés de variables normales centrées et réduites indépendantes 2 à 2, mais il n’en est pas pour autant la conséquence directe : en particulier les variables
 ne sont pas indépendantes entre elles.
ne sont pas indépendantes entre elles.Pour n grand, la variance
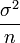 de
de 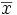 tend vers 0, et la valeur d’une réalisation de
tend vers 0, et la valeur d’une réalisation de 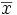 constitue ainsi une estimation de l’espérance μ, qui est également l’espérance de la loi normale suivie par les variables x1, …, x n. Néanmoins, seule la connaissance préalable de la variance σ² de cette loi permet de caractériser un intervalle de confiance pour la variable
constitue ainsi une estimation de l’espérance μ, qui est également l’espérance de la loi normale suivie par les variables x1, …, x n. Néanmoins, seule la connaissance préalable de la variance σ² de cette loi permet de caractériser un intervalle de confiance pour la variable 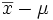 .
.Par contre, il est possible de caractériser un intervalle de confiance rigoureux pour la variable suivante :
avec
En effet, moyennant quelques simplifications, la variable T0 peut se réécrire comme
avec
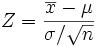 .
.
la variable Z suit la loi normale centrée et réduite, et nous avons vu ci-dessus que la variable s suit la loi du χ² à n - 1 degrés de liberté. De plus, il est possible de démontrer que Z et s sont indépendantes. Par définition, T0 suit donc la loi de Student à k = n - 1 degrés de liberté.
La distribution de la variable T0 est donc connue indépendamment de σ², et par conséquent les intervalles de confiance qui lui sont associés sont également connus. Ainsi, il est possible d’obtenir un intervalle de confiance pour μ à partir d’une réalisation des variables x1, …, xn, de laquelle on déduit des valeurs de
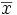 et S. La suite de ce chapitre détaille la procédure permettant la détermination de cet intervalle de confiance.
et S. La suite de ce chapitre détaille la procédure permettant la détermination de cet intervalle de confiance.Pour une variable T suivant la loi de Student à k degrés de liberté, on définit tγk comme
- la quantité telle que la probabilité d’obtenir T > tγk soit égale à γ.
Ceci revient à imposer que 1-γ soit l'image de tγk par la fonction de répartition de la loi de Student. La quantité tγk est également appelé le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (voir tableau des valeurs de tγk ci-dessous).
Dans ce cadre, si tγk > 0, alors la probabilité d’obtenir -tγk < T0 < tγk est égale à 1-2γ.
Or on a
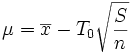 .
.
La probabilité d’obtenir
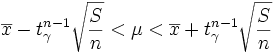 est elle aussi égale à 1-2γ. Le niveau de confiance α associé à cet intervalle est donc α = 1-2γ.
est elle aussi égale à 1-2γ. Le niveau de confiance α associé à cet intervalle est donc α = 1-2γ.Le niveau de confiance α correspond à la probabilité que l’espérance μ de la loi normale se trouve à l’intérieur de l’intervalle de confiance. Par exemple pour α = 0,95, on a un niveau de confiance de 95 %, correspondant à γ = (1-α)/2 = 0,025.
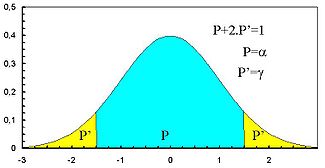
La courbe ci-dessous illustre la notion de niveau de confiance en représentant celui-ci comme une intégrale (aire de la zone en bleu).
Dans la courbe ci-dessus, les frontières entre la zone centrale et les deux zone latérales identiques correspondent à t = tγk et t = -tγk .
En résumé, l’intervalle de confiance de l’espérance μ d’une loi normale de variance quelconque inconnue peut être déterminé à partir des valeurs de n variables indépendantes x1, …, xn suivant toutes cette même loi. Pour un niveau de confiance donné α, cet intervalle est le suivant :
![\left[\,\overline{x} - t_{(1 - \alpha)/2}^{n-1}\sqrt{\frac{S}{n}}, \overline{x} + t_{(1 - \alpha)/2}^{n-1}\sqrt{\frac{S}{n}}\,\right]](/pictures/frwiki/54/6855c76af40da02ac624da9a82e8d259.png) ,
,
avec
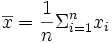 ,
,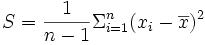 ,
,
et
- tγk le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (dont la définition exacte est donnée ci-dessus).
Distributions apparentées
- X˜t(k = 1) suit une Loi de Cauchy: X˜Cauchy(0,1).
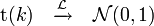 La loi de Student converge en distribution vers la loi normale.
La loi de Student converge en distribution vers la loi normale.- Si
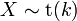 suit une loi de Student alors X2 suit une loi de Fisher:
suit une loi de Student alors X2 suit une loi de Fisher: 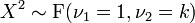
- X˜t(k) a une distribution de Student si
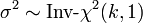 suit une scale-inverse-chi-square distribution (en) et
suit une scale-inverse-chi-square distribution (en) et 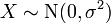 suit une loi normale.
suit une loi normale.
Tableau des valeurs du quantile
Un tableau des valeurs du quantile en fonction de γ et k est fourni ci-dessous.
ν 75% 80% 85% 90% 95% 97.5% 99% 99.5% 99.75% 99.9% 99.95% 1 1.000 1.376 1.963 3.078 6.314 12.71 31.82 63.66 127.3 318.3 636.6 2 0.816 1.061 1.386 1.886 2.920 4.303 6.965 9.925 14.09 22.33 31.60 3 0.765 0.978 1.250 1.638 2.353 3.182 4.541 5.841 7.453 10.21 12.92 4 0.741 0.941 1.190 1.533 2.132 2.776 3.747 4.604 5.598 7.173 8.610 5 0.727 0.920 1.156 1.476 2.015 2.571 3.365 4.032 4.773 5.893 6.869 6 0.718 0.906 1.134 1.440 1.943 2.447 3.143 3.707 4.317 5.208 5.959 7 0.711 0.896 1.119 1.415 1.895 2.365 2.998 3.499 4.029 4.785 5.408 8 0.706 0.889 1.108 1.397 1.860 2.306 2.896 3.355 3.833 4.501 5.041 9 0.703 0.883 1.100 1.383 1.833 2.262 2.821 3.250 3.690 4.297 4.781 10 0.700 0.879 1.093 1.372 1.812 2.228 2.764 3.169 3.581 4.144 4.587 11 0.697 0.876 1.088 1.363 1.796 2.201 2.718 3.106 3.497 4.025 4.437 12 0.695 0.873 1.083 1.356 1.782 2.179 2.681 3.055 3.428 3.930 4.318 13 0.694 0.870 1.079 1.350 1.771 2.160 2.650 3.012 3.372 3.852 4.221 14 0.692 0.868 1.076 1.345 1.761 2.145 2.624 2.977 3.326 3.787 4.140 15 0.691 0.866 1.074 1.341 1.753 2.131 2.602 2.947 3.286 3.733 4.073 16 0.690 0.865 1.071 1.337 1.746 2.120 2.583 2.921 3.252 3.686 4.015 17 0.689 0.863 1.069 1.333 1.740 2.110 2.567 2.898 3.222 3.646 3.965 18 0.688 0.862 1.067 1.330 1.734 2.101 2.552 2.878 3.197 3.610 3.922 19 0.688 0.861 1.066 1.328 1.729 2.093 2.539 2.861 3.174 3.579 3.883 20 0.687 0.860 1.064 1.325 1.725 2.086 2.528 2.845 3.153 3.552 3.850 21 0.686 0.859 1.063 1.323 1.721 2.080 2.518 2.831 3.135 3.527 3.819 22 0.686 0.858 1.061 1.321 1.717 2.074 2.508 2.819 3.119 3.505 3.792 23 0.685 0.858 1.060 1.319 1.714 2.069 2.500 2.807 3.104 3.485 3.767 24 0.685 0.857 1.059 1.318 1.711 2.064 2.492 2.797 3.091 3.467 3.745 25 0.684 0.856 1.058 1.316 1.708 2.060 2.485 2.787 3.078 3.450 3.725 26 0.684 0.856 1.058 1.315 1.706 2.056 2.479 2.779 3.067 3.435 3.707 27 0.684 0.855 1.057 1.314 1.703 2.052 2.473 2.771 3.057 3.421 3.690 28 0.683 0.855 1.056 1.313 1.701 2.048 2.467 2.763 3.047 3.408 3.674 29 0.683 0.854 1.055 1.311 1.699 2.045 2.462 2.756 3.038 3.396 3.659 30 0.683 0.854 1.055 1.310 1.697 2.042 2.457 2.750 3.030 3.385 3.646 40 0.681 0.851 1.050 1.303 1.684 2.021 2.423 2.704 2.971 3.307 3.551 50 0.679 0.849 1.047 1.299 1.676 2.009 2.403 2.678 2.937 3.261 3.496 60 0.679 0.848 1.045 1.296 1.671 2.000 2.390 2.660 2.915 3.232 3.460 80 0.678 0.846 1.043 1.292 1.664 1.990 2.374 2.639 2.887 3.195 3.416 100 0.677 0.845 1.042 1.290 1.660 1.984 2.364 2.626 2.871 3.174 3.390 120 0.677 0.845 1.041 1.289 1.658 1.980 2.358 2.617 2.860 3.160 3.373 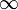
0.674 0.842 1.036 1.282 1.645 1.960 2.326 2.576 2.807 3.090 3.291 Remarque : la dernière ligne du tableau ci-dessus correspond aux grandes valeurs de k. Il s’agit d’un cas limite pour lequel la loi de Student est équivalente à la loi normale centrée et réduite.
Notes
Voir aussi
Articles connexes
Liens externes
- [pdf] La Loi du khi-2, la loi de Student, la loi de Fisher, Université Laval, Département de mathématiques et de statistique
- Ce document en français contient en particulier la dérivation de l'expression de la densité de probabilité ƒT, la démonstration de la distribution de la variable s suivant la loi de Student à n-1 degrés de liberté, ainsi que la démonstration de l'indépendance de s et Z.
- Portail des probabilités et des statistiques
Catégorie : Loi de probabilité
Wikimedia Foundation. 2010.