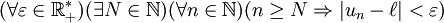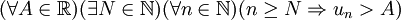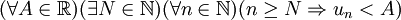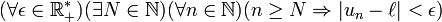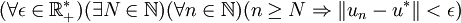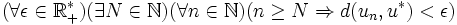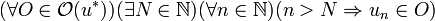Suite convergente

Limite de suite

De manière intuitive, la limite d'une suite est l'élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n'est guère exploitable car il faudrait pouvoir définir le sens de "se rapprocher". Cette notion sous-entend l'existence d'une distance (la valeur absolue dans R, la norme dans C) mais on verra que l'on peut même s'en passer pourvu qu'on ait une topologie. Dans cet article seront présentées d'abord la notion de limite de suite réelle, puis celle de suite complexe et seulement après, quitte à être redondant, celle de limite sur un espace topologique.

Un peu d'histoire

Si la formalisation de la limite d'une suite vient assez tard, son utilisation intuitive date de plus de 2 000 ans. Dans les Éléments d'Euclide (X.1) on peut lire : Étant données deux grandeurs inégales, si, de la plus grande on retranche plus que la moitié, et que du reste on retranche plus que la moitié et si l'on continue toujours ainsi, nous aboutirons à une grandeur inférieure à la plus petite des grandeurs donnée. En langage actuel, cela donnerait :

soit

(u n)

une suite de réels positifs tel que , pour tout n, 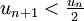$u_{n + 1}<\tfrac{u_n}{2}$ , alors , pour tout réel positif e, il existe un indice n tel que

u n < e

. Ce qui est presque la définition d'une suite ayant pour limite 0.

D'aucuns pourraient croire que cette interprétation du dixième élément d'Euclide est une modernisation fallacieuse, il suffit pour les détromper de regarder l'utilisation qu'en fait Archimède dans ses méthode de quadrature. Cherchant à calculer l'aire du disque ou l'aire sous une parabole, par exemple, il cherche à l'approcher par des aires de polygones et observe alors la différence entre l'aire cherchée et l'aire du polygone. Il démontre qu'à chaque étape, cette différence a été réduite de plus de la moitié et c'est ainsi qu'il conclut qu'en continuant indéfiniment le processus on sera aussi proche qu'on le souhaite de l'aire cherchée. C'est la méthode dite de l'exhaustion.

Cette intuition de la limite mal formalisée ne permettra cependant pas de lever le paradoxe de Zénon d'Élée : Achille part avec un handicap A et court deux fois plus vite que la tortue. Quand il arrive au point de départ de la tortue, celle-ci a déjà parcouru la distance A/2, Achille parcourt alors la distance A/2 mais la tortue a parcouru la distance A/4, à ce train là Achille ne rattrape la tortue qu'au bout d'un nombre infini de processus c'est-à-dire jamais.

Il faut attendre ensuite 1600 ans et les travaux de Grégoire de Saint-Vincent pour entrevoir une tentative de formalisation imparfaite, puis le calcul infinitésimal de Newton et Leibniz.

Limite d'une suite réelle

Suite convergente

On dit qu'une suite converge vers un réel $\ell$ si et seulement si

pour tout intervalle ouvert I , si I contient la limite $\ell$ alors I contient aussi tous les termes de la suite sauf un nombre fini d'entre eux (i.e. contient tous les termes de la suite à partir d'un certain rang).

Cette définition se traduit mathématiquement par :

$(\forall \varepsilon \in \mathbb R_+^*)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow |u_n - \ell| <\varepsilon)$

On écrit alors

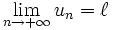$\lim_{n \to + \infty}u_n = \ell$ ou plus simplement, quand il n'y a pas ambiguïté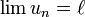 $\lim u_n = \ell$

De cette définition, on peut déduire que

la limite est unique (car les termes de la suite ne peuvent pas se trouver dans deux intervalles disjoints)
toute suite convergente est bornée
une suite encadrée par deux suites convergeant vers la même limite $\ell$ converge aussi vers $\ell$ , c'est le théorème des gendarmes.

Les propriétés de complétude de $\R$ permettent aussi d'affirmer que

Toute suite monotone bornée est convergente.
toute suite de Cauchy est une suite convergente.
Deux suites adjacentes convergent et ont la même limite.

Exemples de suites convergentes

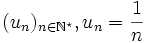La suite : $(u_n)_{n\in\mathbb N^\star}, u_n={1\over n}$ converge vers $0$ .
Si $| q | < 1$ alors la suite : $(u_n)_{n\in\mathbb N}, u_n={q^n}$ converge vers $0$ .
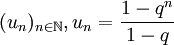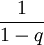Si $| q | < 1$ alors la suite $(u_n)_{n\in\mathbb N}, u_n={1-q^n\over{1 - q}}$ (somme des termes de la suite géométrique de raison $q$ ) converge vers $1\over{1-q}$ .

Une suite qui ne converge pas est appelée suite divergente.

Limite infinie

On dit qu'une suite tend vers $+\infty$ si et seulement si

pour tout intervalle ouvert I , si $I = ]A , +\infty[$ alors I contient aussi tous les termes de la suite sauf un nombre fini d'entre eux (i.e. contient tous les termes de la suite à partir d'un certain rang)

Cette définition se traduit mathématiquement par :

$(\forall A \in \mathbb R)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow u_n > A)$

On écrit alors

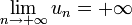$\lim_{n \to + \infty}u_n =+ \infty$ ou plus simplement, quand il n'y a pas ambiguïté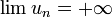 $\lim u_n = +\infty$

On dit qu'une suite tend vers $-\infty$ si et seulement si

pour tout intervalle ouvert I , si $I = ] -\infty, A[$ alors I contient aussi tous les termes de la suite sauf un nombre fini d'entre eux (i.e. contient tous les termes de la suite à partir d'un certain rang)

Cette définition se traduit mathématiquement par :

$(\forall A \in \mathbb R)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow u_n < A)$

On écrit alors

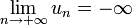$\lim_{n \to + \infty}u_n = -\infty$ ou plus simplement, quand il n'y a pas ambiguïté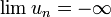 $\lim u_n = -\infty$

L'exemple fondamental d'une suite tendant vers l'infini est celui de l'inverse d'une suite de signe constant et tendant vers 0:

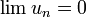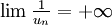S'il existe N tel que, pour tout n > N, $u n > 0$ et si $\lim u_n = 0$ alors $\lim \tfrac{1}{u_n} = +\infty$ .
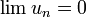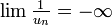S'il existe N tel que, pour tout n > N, $u n < 0$ et si $\lim u_n = 0$ alors $\lim \tfrac{1}{u_n} = -\infty$ .

Deux résultats sont assez faciles à obtenir :

toute suite croissante non majorée tend vers $+ \infty$ et toute suite décroissante non minorée tend vers $- \infty$
toute suite supérieure à une suite tendant vers $+ \infty$ tend vers $+ \infty$ et toute suite inférieure à une suite tendant vers $- \infty$ tend vers $- \infty$

Exemples de suites n'admettant pas de limite

Certaines suites, non seulement sont divergentes mais n'admettent pas de limite. C'est le cas, par exemple,

des suites géométriques de raison inférieure à -1 : la suite (1, -2, 4, -8, 16, -32...) diverge et ne tend ni vers $-\infty$ ni vers $+ \infty$
de la suite (sin(n)), suite bornée n'admettant pas de limite
d'un certain nombre de suites logistiques au comportement chaotique

Opérations sur les limites

Article détaillé : opérations sur les limites.

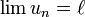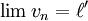On démontre que les opérations sur les suites convergentes se transmettent à leurs limites pour peu que l'opération ait un sens. Mathématiquement parlant, cela signifie que si $\lim u_n = \ell$ et si $\lim v_n = \ell '$ alors

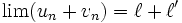
$\lim (u_n +v_n) = \ell + \ell '$
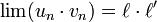
$\lim (u_n \cdot v_n) = \ell \cdot \ell '$
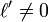
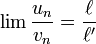
Si $\ell' \neq 0$ $\lim \frac{u_n}{v_n} = \frac{\ell}{\ell '}$

De plus, si f est une fonction continue en $\ell$ et si $f (u n)$ est définie alors 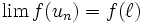$\lim f(u_n) = f(\ell)$

L'intervention de suites tendant vers 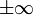$\pm \infty$ rend les calculs un peu plus compliqués:

Somme :
- si une suite converge et l'autre tend vers l'infini, la somme a même limite que la suite tendant vers l'infini.
- si les deux suites tendent vers le même infini, il en est de même de leur somme
- si les deux suites tendent vers deux infinis différents, on ne peut pas conclure directement, on dit alors que l'on tombe sur une forme indéterminée
Produit: on pourra, à condition qu'une limite existe, appliquer la règle des signes
- Si une suite converge vers un réel non nul et l'autre tend vers l'infini, le produit tendra vers un infini dont le signe se détermine par la règle des signes
- Si les deux suites tendent vers l'infini, il en sera de même de leur produit.
- Si une des suites tend vers 0 et l'autre vers l'infini, on ne peut pas conclure directement, c'est une seconde forme indéterminée.
Inverse
- Si une suite tend vers l'infini alors son inverse converge vers 0
- Si une suite, de signe constant, converge vers 0 alors son inverse tend vers l'infini

Limite d'une suite complexe

On dit qu'une suite converge vers un complexe $\ell$ si et seulement si

$(\forall \epsilon \in \mathbb R_+^*)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow |u_n - \ell| <\epsilon)$

On remarque qu'il s'agit de la même définition que dans $\R$ , au détail près qu'il ne s'agit plus de valeur absolue mais de module.

On écrit alors

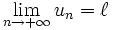$\lim_{n \to + \infty}u_n = \ell$ ou plus simplement, quand il n'y a pas ambiguïté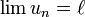 $\lim u_n = \ell$

On retrouve pour les suites complexes convergentes, les mêmes propriétés que pour les suites réelles, exceptées celles liées à la relation d'ordre : la limite est unique, une suite convergente est de module borné, toute suite de Cauchy converge (en effet $\mathbb C$ est aussi complet), les différentes opération comme somme, produit, quotient se transmettent bien à la limite.

Autres espaces

Espace vectoriel normé

Dans un espace vectoriel normé, on dit qu'une suite $(u n)$ converge vers $u *$ si et seulement si

$(\forall \epsilon \in \mathbb R_+^*)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow \|u_n - u^*\| <\epsilon)$

On remarque qu'il s'agit de la même définition que dans $\R$ , au détail près qu'il ne s'agit plus de valeur absolue mais de norme.

On écrit alors

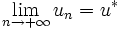$\lim_{n \to + \infty}u_n = u^*$ ou plus simplement, quand il n'y a pas ambiguïté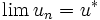 $\lim u_n = u^*$

L'unicité de la limite est conservée ainsi que la transmission à la limite de la somme et de la multiplication par k. Ce n'est que dans un espace vectoriel normé complet que l'on pourra affirmer que toute suite de Cauchy converge.

Espace métrique

Dans un espace métrique, on dit qu'une suite $(u n)$ converge vers $u *$ si et seulement si

$(\forall \epsilon \in \mathbb R_+^*)(\exists N \in \mathbb N) (\forall n \in \mathbb N) (n \geq N \Rightarrow d(u_n,u^*) <\epsilon)$

On remarque qu'il s'agit de la même définition que dans $\R$ , au détail près qu'il ne s'agit plus de valeur absolue d'une différence mais de distance.

On écrit alors

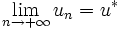$\lim_{n \to + \infty}u_n = u^*$ ou plus simplement, quand il n'y a pas ambiguïté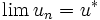 $\lim u_n = u^*$

Seule l'unicité de la limite est conservée. Il faudra être dans un espace métrique complet pour pouvoir dire que toute suite de Cauchy converge. Si une opération existe sur l'espace en question, il faudra qu'elle soit continue pour se transmettre à la limite.

Espace topologique

Toutes les définitions précédentes se rejoignent dans la définition de la convergence dans un espace topologique.

Soit $E\,$ un espace muni d'une topologie 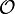$\mathcal O$ . On note 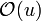$\mathcal O(u)$ l'ensemble des ouverts contenant $u\,$ .
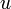On dira que la suite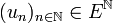 $(u_n)_{n\in\mathbb N}\in E^{\mathbb N}$ est une suite convergente vers 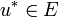$u^*\in E$ si

$(\forall O\in\mathcal O(u^*))(\exist N\in \mathbb N)(\forall n \in \mathbb N)(n > N \Rightarrow u_n \in O)$

Il faudra être dans un espace topologique séparé pour pouvoir affirmer que la limite est unique.

Valeurs d'adhérence

Cette section ne traite que le cas des suites à valeurs dans un espace métrique

Article détaillé : Valeur d'adhérence.

Définitions

Soit 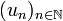$(u_n)_{n \in \mathbb N }$ une suite à valeurs dans un espace métrique $(E, d)$ .
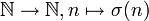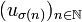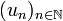Si $\mathbb N \rightarrow \mathbb N , n \mapsto \sigma(n)$ est une fonction strictement croissante (une telle fonction s'appelle une extractrice), on dit que la suite $(u_{\sigma(n)})_{n \in \mathbb N }$ est une suite extraite (ou sous-suite) de la suite $(u_n)_{n \in \mathbb N }$ .
Grosso modo, c'est la suite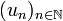 $(u_n)_{n \in \mathbb N }$ pour laquelle on n'a gardé que certains termes (une infinité quand même).

On dit que la valeur l est une valeur d'adhérence de la suite 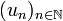$(u_n)_{n\in \mathbb N}$ si et seulement s’il existe une suite extraite de 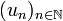$(u_n)_{n\in \mathbb N}$ qui converge vers l.
Pour se faire une idée, une valeur d'adhérence est un élément « près duquel la suite passe souvent », c'est-à-dire qu'aussi loin qu'on aille, on trouvera toujours un terme de la suite près de cet élément.

Propriétés

Propriété 1

Soit 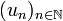$(u_n)_{n \in \mathbb N}$ une suite à valeurs dans E.
Si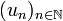 $(u_n)_{n \in \mathbb N}$ converge vers 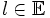$l \in \mathbb E$ , l est l'unique valeur d'adhérence de 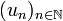$(u_n)_{n \in \mathbb N}$ , c'est-à-dire que toutes les suites extraites 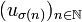$(u_{\sigma(n)})_{n \in \mathbb N }$ convergent vers $l$

Dans le cas où E est un espace compact, on dispose même d'une réciproque:

Propriété 2

Soit 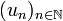$(u_n)_{n \in \mathbb N}$ une suite à valeurs dans un espace métrique compact, qui ne possède qu'une unique valeur d'adhérence l. Alors 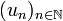$(u_n)_{n \in \mathbb N}$ est convergente de limite l.

Propriété 3

Soit 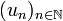$(u_n)_{n \in \mathbb N}$ une suite à valeurs dans E.
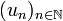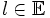$(u_n)_{n \in \mathbb N}$ converge vers $l \in \mathbb E$ si et seulement si :

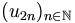$(u_{2n})_{n \in \mathbb N}$ converge vers $l$
$(u_{2n+1})_{n \in \mathbb N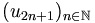}$ converge vers $l$

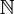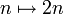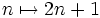On voit d'ailleurs bien comment généraliser ce résultat: il faut en fait que les images des extractrices considérées recouvrent entièrement $\mathbb N$ (par exemple, ici, $n \mapsto 2n$ et $n \mapsto 2n+1$ ).

Remarque

Cette propriété est utile pour démontrer la non-convergence d'une suite :
si on considère une suite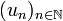 $(u_n)_{n \in \mathbb N}$ à valeurs dand E et si :

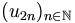$(u_{2n})_{n \in \mathbb N}$ converge vers $l 1$
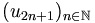$(u_{2n+1})_{n \in \mathbb N}$ converge vers $l 2$ avec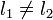 $l_1 \ne l_2$

Alors 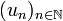$(u_n)_{n \in \mathbb N}$ ne converge pas

Exemple La suite : 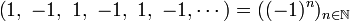$\left(1, \ -1, \ 1, \ -1, \ 1, \ -1, \cdots\right)= ((-1)^n)_{n\in\mathbb N}$ est décomposable en deux sous-suites :

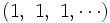$\left(1, \ 1, \ 1, \cdots\right)$ converge vers 1
$\left(-1, \ -1, \ -1, \cdots\right)$ converge vers -1

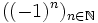
Les deux sous-suites convergeant vers des limites différentes, la suite initiale ne converge pas. Par contre, -1 et 1 sont des valeurs d'adhérence de $((-1)^n)_{n\in\mathbb N}$

Théorème de Bolzano-Weierstrass

Toujours lorsque E est un espace compact, on dispose du puissant théorème de Bolzano-Weierstrass. Il s'applique, par exemple, si 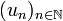$(u_n)_{n \in \mathbb N}$ est à valeurs dans un segment de $\mathbb R$ (autrement dit si c'est une suite réelle bornée):

Si 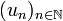$(u_n)_{n\in \mathbb N}$ est une suite à valeurs dans un espace métrique compact E, alors $(u_n)_{n\in \mathbb N}$ admet une valeur d'adhérence dans E.

Portail des mathématiques

Ce document provient de « Limite de suite ».

Catégories : Analyse réelle | Suite

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Suite convergente de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Suite de cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une … Wikipédia en Français
suite — [ sɥit ] n. f. • XIIIe; siute « poursuite en justice » 1080; a. p. p. de suivre; lat. pop. sequitus I ♦ A ♦ Action de poursuivre. 1 ♦ Dr. Droit de suite : droit qui permet au créancier hypothécaire de suivre l immeuble hypothéqué dans les mains… … Encyclopédie Universelle
Suite bornee — Suite bornée Une suite réelle est dite bornée si : ou de façon équivalent si : Autrement dit, l ensemble des ses termes est compris entre une borne supérieure et une borne inférieure. On peut déduire de façon immédiate qu une suite… … Wikipédia en Français
Suite (mathématiques) — Pour les articles homonymes, voir Suite. En mathématiques, une suite[1] est une famille d éléments indexée par les entiers naturels. Une suite finie est une famille indexée par les entiers strictement positifs inférieurs ou égaux à un certain… … Wikipédia en Français
Suite divergente — Limite de suite De manière intuitive, la limite d une suite est l élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n est guère exploitable car il faudrait pouvoir définir le… … Wikipédia en Français
Suite de Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une suite de réels, de complexes, de points d … Wikipédia en Français
Suite logistique — En mathématiques, une suite logistique est un exemple simple de suite dont la récurrence n est pas linéaire. Souvent citée comme exemple de la complexité pouvant surgir de simple relation non linéaire, cette suite fut popularisée par le… … Wikipédia en Français
Suite bornée — Une suite réelle est dite bornée si : ou de façon équivalent si : Autrement dit, l ensemble de ses termes est compris entre une borne supérieure et une borne inférieure. On peut déduire de façon immédiate qu une suite bornée ne diverge… … Wikipédia en Français
Suite extraite — Sous suite En mathématiques, une sous suite (ou une suite extraite) est une suite obtenue en ne prenant que certains éléments (une infinité) d une suite de départ. Cette opération est parfois appelée extraction. Formellement, une suite est une… … Wikipédia en Français
convergente — ● convergent, convergente adjectif (latin convergens) Qui converge, tend vers un point unique : Rayons convergents. Se dit d actions qui tendent vers le même but, le même résultat, ou de données abstraites présentant de l analogie : Points de vue … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Suite convergente

Limite de suite

Sommaire

Un peu d'histoire