Quadrature de la parabole

Segment de parabole

La quadrature de la parabole est le calcul de l'aire d'un segment de parabole, surface délimitée par une parabole et une droite. Elle est réalisée par Archimède (-287 à -212), d'une part en utilisant la méthode d'exhaustion d'Eudoxe (-406 à -355) en approximant la surface du segment par des triangles, d'autre part par une méthode originale par pesée, figurant dans un palimpseste découvert seulement en 1906.

C'est un des premiers calculs d'intégration en mathématiques. Il apparaît dans une lettre d'Archimède à Dositée.

Sommaire

1 Calcul moderne
2 Calcul d'Archimède par la méthode d'exhaustion
- 2.1 Principe
- 2.2 Développement
3 Quadrature par la méthode des pesées
4 Voir aussi
5 Sources

Calcul moderne

Soit $y = \dfrac{x^2}{2p}$ , l'équation de la parabole.

L'aire de la surface située sous l'arc projeté en abscisse sur l'intervalle $[0, x 0]$ est par intégration:

$A = \int_0^{x_0}\dfrac{x^2}{2p}\,dx = \left[\dfrac{1}{3}\dfrac{x^3}{2p}\right]_0^{x_0}= \dfrac{1}{3} \dfrac{x_0^3}{2p} = \dfrac{1}{3}y_0 x_0$ avec $y_0 = \dfrac{x_0^2}{2p}$

Calcul d'Archimède par la méthode d'exhaustion

Principe

En mathématiques grecques, les calculs d'aire se font essentiellement par approximation au moyen d'une méthode dite par exhaustion, reposant sur un double raisonnement par l'absurde. On approche la surface du segment de parabole par des triangles intérieurs à la parabole, cette approximation pouvant être rendue aussi précise que désirée.

Développement

Archimède cherche à calculer l'aire P du triangle curviligne entre les points d'abscisse a et d'abscisse b, l'axe de la parabole étant l'axe des ordonnées. Il dessine alors un triangle passant par les points d'abscisse a, d'abscisse b et d'abscisse $\dfrac{a + b }{2}$ . Il décide donc d'approcher P par l'aire S de ce grand triangle. Puis il recommence dans les petits triangles curvilignes laissés pour compte.

Il démontre que l'aire de chaque petit triangle est égal au huitième de l'aire du grand triangle, en démontrant que la distance horizontale a été divisée par deux, tandis que la flèche a été divisée par 4. Il peut alors approcher P par l'aire du grand triangle et des deux petits : $S + \dfrac S4$ , puis, continuant ainsi, il approche l'aire de la parabole par $S n$ .

$S_n= S + \dfrac S4 + \dfrac{S}{16} + ...+ \dfrac{S}{4^n}$ .

On sait, dès cette époque, que $S n$ peut s'écrire

$S_n=\dfrac 43 S - \dfrac 13 \dfrac{S}{4^n}$

mais on ne sait pas passer à la limite. On sait seulement utiliser le principe d'exhaustion, en s'appuyant sur l'axiome d'Archimède :

Axiome d'Archimède : étant données deux grandeurs inégales, si de la plus grande on retranche plus que sa moitié puis du reste ainsi obtenu on retranche encore plus que sa moitié et si l'on continue toujours ainsi, nous aboutirons finalement à une grandeur inférieure à la plus petite des grandeurs données.

Archimède envisage alors 3 possibilités : ou bien P est plus grande que $\dfrac 43 S$ , ou bien P est plus petite que $\dfrac 43 S$ , ou bien P égale $\dfrac 43 S$

Si P était plus grande que $\dfrac 43 S$

Il démontre que la différence entre P et

S n

peut être rendue aussi petite que l'on souhaite. En effet, à l'aire de la parabole, on retranche l'aire du triangle qui représente plus de la moitié de l'aire de la parabole car l'aire du triangle vaut exactement la moitié de l'aire du parallélogramme dessiné, aire plus grande que l'aire de la parabole. Et ainsi de suite à chaque étape. Il peut donc rendre

P - S n

plus petite que $P - \dfrac 43 S$ . Ce qui voudrait dire que

S n

serait supérieure à $\dfrac 43 S$ . Impossible d'après l'expression de

S n

Si P est inférieure à $\dfrac 43 S$

Selon le même principe d'exhaustion, on peut rendre la différence $\dfrac 43 S - S_n$ aussi petite que l'on veut, puisque à chaque étape on retranche les 3/4 de ce qui reste. On pourrait donc la prendre plus petite que $\dfrac 43 S - P$ . Ce qui voudrait dire que

S n

serait plus grande que P. Impossible puisque les triangles sont intérieurs au segment de parabole.

Les deux cas étant éliminés, il ne reste plus que le cas $P = \dfrac 43 S$

Il est intéressant de voir que le terme "aussi petite qu'on le souhaite" est très proche de la notion de limite qu'Archimède ne connaît pas. Il est donc contraint de raisonner par l'absurde pour prouver son égalité.

Quadrature par la méthode des pesées

Archimède propose dans le même ouvrage une présentation mécanique de la quadrature qui démontre son génie mécanique . Cette démarche figure dans un unique manuscrit du texte d'Archimède, découvert dans un palimpseste en 1906.

Il décide de peser la parabole par un système de levier.

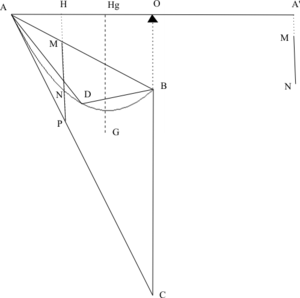
La figure présentée ici est une simplification de celle figurant dans l'ouvrage d'Archimède. La droite (AC) est tangente en A à la parabole, le segment [BC] est parallèle à l'axe de la parabole. Le point D se projette, parallèlement à l'axe de la parabole, sur le milieu de [AB].

L'idée est d'équilibrer le triangle ABC, suspendu en son centre de gravité G par une masse placée en A'.

Archimède procède par segment. Le triangle ABC suspendu en Hg peut être remplacé par une multitude de segments MP suspendus en H. Archimède a déjà démontré (traité sur les paraboles) que MN est à MP ce que BM est à BA. On dirait maintenant :

$\dfrac{MN}{MP}=\dfrac{BM}{BA}$ . (1)

Grâce au théorème de Thalès, on a aussi l'égalité

$\dfrac{BM}{BA}= \dfrac{OH}{OA}$ (2)

Donc

$\dfrac{MN}{MP}=\dfrac{OH}{OA} = \dfrac{OH}{OA'}$

Puis :

$OH \times MP = OA' \times MN$

Le segment [MN] placé en A' équilibre donc le segment [MP] placé en H.

Segment par segment, il équilibre donc le triangle ABC placé en Hg par la portion de parabole placée en A' . Donc

Aire de la parabole $\times$ OA' = Aire du triangle $\times$ OHg.

Comme $OHg = \dfrac 13 OA$ alors

Aire de la parabole = $\dfrac 13$ aire de ABC.

Enfin, dans le même traité sur les paraboles, Archimède a déjà démontré que l'aire de ABC vaut 4 fois l'aire de ABD.

L'aire de la parabole vaut donc $\dfrac 43$ de l'aire du triangle ABD

Voir aussi

La quadrature de la parabole pour le traité d'Archimède

Sources

Histoire des mathématiques, routes et dédales, Dahan-Dalmédico et Pfeiffer, ed. Point-sciences.
La démonstration mathématique dans l'histoire, ed. Irem de Lyon
[PDF]Quadrature de la parabole
[PDF]Quadrature par la méthode des pesées, séminaire de mathématiques, IUFM de La Réunion.

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Quadrature de la parabole de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

La quadrature de la parabole — Un segment de parabole Sur les autres projets Wikimedia : « La quadrature de la parabole », sur le Wiktionnaire (dictionnaire universel) La quadrature de la parabole est un traité de géo … Wikipédia en Français
Quadrature (mathematiques) — Quadrature (mathématiques) Pour les articles homonymes, voir Quadrature. En mathématiques, la quadrature d une surface est la recherche d un carré ayant même aire que la surface en question. Si dans le langage courant le terme de quadrature revêt … Wikipédia en Français
PARABOLE — PARABOLE, religion Récit allégorique, habituellement assez bref, sous lequel, dans les textes néo testamentaires et spécialement dans les Évangiles, se cache un enseignement, selon un procédé populaire et oriental consistant à faire passer un… … Encyclopédie Universelle
quadrature — [ k(w)adratyr ] n. f. • 1407; bas lat. quadratura 1 ♦ Géom. Opération qui consiste à construire un carré équivalant à une aire donnée. Cour. La quadrature [ kadratyr ] du cercle : faux problème que les géomètres anciens tentaient de résoudre. Fig … Encyclopédie Universelle
parabole — 1. (pa ra bo l ) s. f. Allégorie qui renferme quelque vérité importante. La parabole a deux parties, le corps et l âme ; le corps est le récit de l histoire qu on a imaginée ; et l âme, le sens moral ou mystique, caché sous les paroles ou récit.… … Dictionnaire de la Langue Française d'Émile Littré
Quadrature (mathématiques) — Pour les articles homonymes, voir Quadrature. En mathématiques, la quadrature d une surface est la recherche d un carré ayant même aire que la surface en question. Si dans le langage courant le terme de quadrature revêt le sens d opération… … Wikipédia en Français
ISLAM - Les mathématiques et les autres sciences — «Et vous avez en ma personne le meilleur barbier de Bagdad, un médecin expérimenté, un chimiste très profond, un astrologue qui ne se trompe point, un grammairien achevé, un parfait rhétoricien, un logicien subtil, un mathématicien accompli dans… … Encyclopédie Universelle
CALCUL INFINITÉSIMAL - Histoire — L’expression «calcul infinitésimal» désigne habituellement l’ensemble des notations et des méthodes fondamentales du calcul différentiel, du calcul intégral et du calcul des variations, tel qu’il a été mis au point au cours des XVIIe et XVIIIe… … Encyclopédie Universelle
Archimede — Archimède Pour les articles homonymes, voir Archimède (homonymie). Archimède … Wikipédia en Français
Archimède de Syracuse — Archimède Pour les articles homonymes, voir Archimède (homonymie). Archimède … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Quadrature de la parabole

Sommaire

Calcul moderne