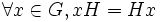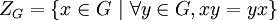Sous-groupe invariant

Sous-groupe invariant

Sous-groupe normal

En théorie des groupes, un sous-groupe normal ou sous-groupe distingué ou sous-groupe invariant H d'un groupe G est un sous-groupe globalement stable par l'action de G sur lui-même par conjugaison. Les sous-groupes normaux interviennent naturellement dans la définition du quotient d'un groupe. Les sous-groupes normaux de G sont exactement les noyaux des morphismes définis sur G.

Un sous-groupe caractéristique de G est un sous-groupe stable par l'action de tous les automorphismes de G. Un tel sous-groupe est toujours normal.

Les sous-groupes normaux connaissent des applications en géométrie dans l'étude des actions de groupes, en topologie algébrique dans la classification des revêtements, en théorie de Galois dans la correspondance de Galois.

Sommaire

Définition

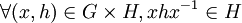On dit que H est un sous-groupe distingué de G s'il est stable par conjugaison, soit \forall (x, h) \in G\times H, x h x^{-1} \in H \,.

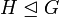On note alors H\trianglelefteq G.

Une façon équivalente de définir un sous-groupe distingué est de dire que les classes à droite et à gauche de H dans G coïncident, c'est-à-dire:

\forall x \in G, x H = H x \,

Si G est abélien, tous les sous-groupes sont distingués.

Lien avec les morphismes de groupes

Le noyau N d'un morphisme de groupes 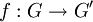f:G\to G' est toujours un sous-groupe normal de G, car pour 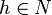h\in N, l'image f(h) est l'élément neutre de G', et donc f(xhx − 1) = f(x)f(x − 1) aussi, pour tout 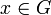x\in G. Réciproquement, tout sous-groupe normal est noyau d'un morphisme de groupes (un tel morphisme est la surjection canonique du groupe dans le groupe quotient). Donc les sous-groupes distingués sont précisément les sous-ensembles qui sont le noyau d'un morphisme de groupes. 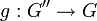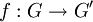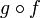Ainsi, si N est un sous-groupe normal et g:G''\to G est un morphisme de groupes, l'image réciproque g − 1(N) est un sous-groupe normal de G'' : on peut voir N comme le noyau d'un morphisme de groupes f:G\to G', et alors g − 1(N) est le noyau du morphisme composée g\circ f.

Article détaillé : homomorphisme de groupes

Groupe quotient

Les sous-groupes distingués sont importants dans l'étude des groupes quotients à cause du résultat suivant:

On peut construire un groupe quotient G / H de loi compatible avec celle de G

si et seulement si

H est un sous-groupe distingué de G.

Article détaillé : Groupe quotient.

Exemples

  • {e} et G sont toujours des sous-groupes normaux (et même caractéristiques) de G. S'ils sont les seuls sous-groupes normaux (et 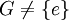G\neq\{e\}), alors G est dit simple.
  • Tout sous-groupe d'un groupe abélien est normal (mais pas toujours caractéristique).
Z_G = \left\{ x \in G\ |\ \forall y \in G, x y = y x \right\}

C'est toujours un sous-groupe normal (et caractéristique) de G.

  • On appelle groupe dérivé de G, noté D(G), le groupe engendré par les commutateurs, soit 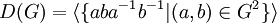D(G)=\langle\{aba^{-1}b^{-1}|(a, b)\in G^2\}\rangle est normal (et caractéristique). C'est le plus petit sous-groupe distingué de G tel que le quotient soit commutatif.
  • Si G est un groupe et H un sous-groupe de G, le coeur de H dans G est défini par 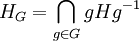H_{G}=\bigcap_{g \in G}{gHg^{-1}}. C'est un sous-groupe de H qui est distingué dans G et qui contient tous les sous-groupes de H qui sont distingués dans G. Si H est d'indice fini n dans G alors le groupe quotient G / HG est isomorphe à un sous-groupe de Sn, le groupe symétrique sur n éléments.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Sous-groupe normal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sous-groupe invariant de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • sous-groupe invariant — invariantinis pogrupis statusas T sritis fizika atitikmenys: angl. invariant subgroup; normal subgroup vok. invariante Untergruppe, f rus. инвариантная подгруппа, f pranc. sous groupe invariant, m …   Fizikos terminų žodynas

  • Sous-groupe invariant d'un groupe — ● Sous groupe invariant d un groupe synonyme de sous groupe distingué …   Encyclopédie Universelle

  • Sous-groupe distingué — Sous groupe normal En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux… …   Wikipédia en Français

  • Sous-groupe normal — En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux interviennent… …   Wikipédia en Français

  • Sous-groupe a un parametre — Sous groupe à un paramètre Un sous groupe à un paramètre d un groupe de Lie réel G est un morphisme de groupes de Lie c:R G. Plus explicitement, c est une application différentiable vérifiant : . En dérivant cette relation par rapport à la… …   Wikipédia en Français

  • Sous-groupe à un paramètre — Un sous groupe à un paramètre d un groupe de Lie réel G est un morphisme de groupes de Lie c:R G. Plus explicitement, c est une application différentiable vérifiant : . En dérivant cette relation par rapport à la variable s et en évaluant en …   Wikipédia en Français

  • sous-groupe non invariant — neinvariantinis pogrupis statusas T sritis fizika atitikmenys: angl. non invariant subgroup vok. nichtinvariante Untergruppe, f rus. неинвариантная подгруппа, f pranc. sous groupe non invariant, m …   Fizikos terminų žodynas

  • invariant — invariant, iante [ ɛ̃varjɑ̃, jɑ̃t ] adj. et n. m. • 1877; de 1. in et varier, par l angl. invariant (1851) ♦ Sc. Se dit d une grandeur, d une expression, d une relation ou d une propriété qui se conserve dans une transformation de nature physique …   Encyclopédie Universelle

  • Groupe Orthogonal — Généralités Soit E un espace vectoriel de dimension finie n sur un corps , muni d une forme quadratique q. Un automorphisme orthogonal pour cette forme quadratique est un automorphisme linéaire f du espace vectoriel E laissant invariant q.… …   Wikipédia en Français

  • Groupe distingué — Sous groupe normal En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”