Sous-groupe caracteristique
- Sous-groupe caracteristique
-
Sous-groupe caractéristique
Étant donné un groupe G, on appelle « sous-groupe caractéristique de G » tout sous-groupe H de G stable par tout automorphisme de G :
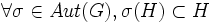 .
.
Propriété
Exemples
- Le sous-groupe dérivé D(G) d'un groupe G est un sous-groupe caractéristique de G.
En effet, pour tout automorphisme σ de G et pour tous 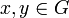 , on a σ([x,y]) = [σ(x),σ(y)].
, on a σ([x,y]) = [σ(x),σ(y)].
- Le centre est lui aussi un groupe caractéristique.
- Généralement un sous-groupe défini par une expression qui ne mentionne aucun élément particulier (autre que l'élément neutre) est caractéristique, car le sens d'une telle expression ne change pas sous un automorphisme quelconque. Ainsi sont distingués:
- Le groupe dérivé, qui est engendré par
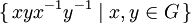 ,
,
- Le centre, qui est défini par la l'expression
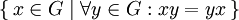 ,
,
- Le sous-groupe engendré par les éléments d'ordre deux (ou d'un autre ordre donné),
- Le sous-groupe engendré par
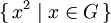 , etc.
, etc.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie des groupes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Sous-groupe caracteristique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Sous-groupe caractéristique — Dans un groupe G, un sous groupe H est dit caractéristique lorsqu il est stable par tout automorphisme de G : pleinement caractéristique lorsqu il est même stable par tout endomorphisme de G : Sommaire … Wikipédia en Français
Sous-groupe distingué — Sous groupe normal En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux… … Wikipédia en Français
Sous-groupe invariant — Sous groupe normal En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux… … Wikipédia en Français
Sous-espace caracteristique — Sous espace caractéristique Définitions Soient E un K espace vectoriel de dimension finie et u un endomorphisme de E. Soit on appelle sous espace caractéristique, sous espace spectral, ou encore espace propre généralisé de associé à la valeur… … Wikipédia en Français
Sous-groupe normal — En théorie des groupes, un sous groupe normal ou sous groupe distingué ou sous groupe invariant H d un groupe G est un sous groupe globalement stable par l action de G sur lui même par conjugaison. Les sous groupes normaux interviennent… … Wikipédia en Français
Sous-groupe de Frattini — Pour les articles homonymes, voir Frattini. Soit G un groupe (au sens mathématique). Les éléments de G qui appartiennent à tout sous groupe maximal de G forment un sous groupe de G, qu on appelle le sous groupe de Frattini de G et qu on note Φ(G) … Wikipédia en Français
Sous-groupe normal minimal — En mathématiques, et plus particulièrement en théorie des groupes, un sous groupe normal minimal d un groupe G est un élément minimal de l ensemble des sous groupes normaux de G non réduits à l élément neutre, cet ensemble étant ordonné par… … Wikipédia en Français
Sous-groupe de Fitting — Soit G un groupe, au sens mathématique. On prouve que si H1, ...., Hn sont des sous groupes normaux nilpotents de G, le sous groupe de G engendré par H1, ...., Hn est lui aussi un sous groupe normal nilpotent de G[1]. Il en résulte que si le… … Wikipédia en Français
Sous-espace caractéristique — Définitions Soient E un K espace vectoriel de dimension finie et u un endomorphisme de E. Soit on appelle sous espace caractéristique, sous espace spectral, ou encore espace propre généralisé de associé à la valeur propre le sous espace … Wikipédia en Français
Sous-groupe de Hall — En théorie des groupes (une branche des mathématiques), les sous groupes de Hall d un groupe fini sont les sous groupes dont l ordre et l indice sont premiers entre eux. Ils portent le nom du mathématicien Philip Hall (en). Sommaire 1… … Wikipédia en Français
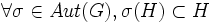 .
.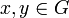 , on a σ([x,y]) = [σ(x),σ(y)].
, on a σ([x,y]) = [σ(x),σ(y)].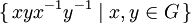 ,
,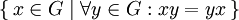 ,
,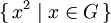 , etc.
, etc.