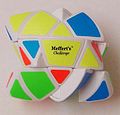
Pyramorphix

Pyramorphix casse-tête
Pyramorphix résolu.
Mécanisme	Rubik's Cube
Joueur(s)	1
habileté physique  Non  réflexion décision  Oui générateur de hasard  Non info. compl. et parfaite  Oui
Pyramorphix mélangé.
modifier

Le Pyramorphix est un casse-tête mécanique tétraédrique équivalent au Pocket Cube.

Il a au total 8 pièces mobiles pouvant être disposées de telle façon:

• chacune des 8 pièces peut être permutée avec une autre, soit 8! permutation
• chaque coins peut être tourné sur lui-même de 3 façon différentes, soit 3⁴ rotations

soit un total de 2 580 480 combinaisons (environ 2,6 millions).

Master Pyramorphix

Il existe également un Master Pyramorphix.

Le Master Pyramorphix est un casse-tête mécanique tétraédrique équivalent au Rubik's Cube 3x3x3. Il a la même architecture interne que le Rubik's Cube, la seule différence étant sa forme extérieure (en découpant un cube d'un centre vers les coins de la face opposés on obtient un tétraèdre). De cette ressemblance ont en déduit que :

• les 4 coins et les centres des 4 faces du tétraèdre sont équivalents aux 8 coins du cube
• les 6 arrêtes du tétraèdre sont équivalents aux 6 centres des faces du cube ( à la différence qu'ici le sens des arrêtes à une importance contrairement aux centres du cube)
• les 12 pièces en forme de trapèze sur le tétraèdre sont équivalents aux 12 arrêtes du cube

Il en résulte pour les combinaisons:

• 8! permutations des coins et des centres du tétraèdre
• chaque coin peut être tourné de 3 manières différentes soit 4³ combinaisons
• les 12 trapèzes ont 12! permutations pour leurs positions
• chacun de ces 12 trapèzes peut être retourné d'un demi-tour, mais le sens du 12ème est déterminé par le sens des 11 autres soit 2¹1 permutations
• enfin les arrêtes du tétraèdres ont :
  • 3 permutations équatoriales (en gardant deux arrêtes à leurs places en en échangeant deux arrêtes qui sont diamétralement opposées)
  • 3 permutations triangulaires (en échangeant les positions de 3 arrêtes entre elles)
  • enfin, chaque arrête peut-être tournée d'un quart de tour et possède donc 4 positions, soit 4⁵ permutations (la rotation de la dernières étant déterminée par celles des 5 autres).

Il y a donc un total de 23 329 738 984 337 178 624 000 (environ 2,33 * 10²² combinaisons)

• 

  Master Pyramorphix résolu.

• 

  Master Pyramorphix avec couleurs mélangées.

• 

  Master Pyramorphix avec couleurs et formes mélangées.

• 

  Master Pyramorphix en extension maximum.

Cliquez sur une vignette pour l’agrandir

Voir aussi

v · Rubik's Cube
Inventeur	Ernő Rubik
Rubik's Cubes	2×2×2 (Pocket Cube) • 3×3×3 (Rubik's Cube) • 4×4×4 (Rubik's Revenge) • 5×5×5 (Professor's Cube) • 6×6×6 (V-Cube 6) • 7×7×7 (V-Cube 7)
Variantes cubiques	Square One • Skewb • Sudoku Cube (en) • Void Cube • Helicopter Cube (en)
Variantes non cubiques	Tétraèdre Pyramorphix • Pyraminx • BrainTwist (en) Octaèdre Skewb Diamond Dodécaèdre Megaminx • Étoile d'Alexandre • Skewb Ultimate • Pyraminx Crystal Icosaèdre Impossiball • Dogic
Dérivés	Rubik's Magic • Rubik's Snake • Missing Link (en) • Rubik's Revolution (en) • Rubik's Clock • Rubik's 360 • Rubik's Triamid (en)
Records et détenteurs	Records du monde • Yu Nakajima • Erik Akkersdijk • Dan Cohen (en) • Feliks Zemdegs
Solveurs	David Singmaster (en) • Jessica Fridrich (en) • Lars Petrus (en) • Ron van Bruchem (en) • Chris Hardwick (en) • Shotaro "Macky" Makisumi (en) • Tyson Mao (en) • Toby Mao (en) • Leyan Lo (en) • Frank Morris (Rubik's Cube) (en)
Solutions	Algorithme de Dieu • Optimal (en) • Speedcubing
Mathématiques	Théorie mathématique sur le Rubik's Cube
Organisation officielle	World Cube Association
Articles liés	Liste des logiciels de Rubik's Cube (en)

• Portail des jeux