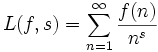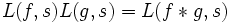Produit de convolution de Dirichlet

Convolution de Dirichlet

Johann Peter Gustav Lejeune Dirichlet développe son produit en 1937 pour démontrer le théorème de la progression arithmétique.

En mathématiques, la convolution de Dirichlet, encore appelée produit de convolution de Dirichlet ou produit de Dirichlet est une loi de composition interne définie sur l'ensemble des fonctions arithmétiques, c'est à dire des fonctions définies sur les entiers strictement positifs et à valeurs dans les nombres complexes^{[Note 1]}. Cette loi de convolution est utilisée en arithmétique, aussi bien algébrique qu'analytique. On la trouve aussi pour résoudre des questions de dénombrements.

Le mathématicien Johann Peter Gustav Lejeune Dirichlet développe ce produit en 1837 pour démontrer le théorème de la progression arithmétique^[1].

Sommaire

1 Définition, exemples et premières propriétés
2 Fonction multiplicative
3 Série L de Dirichlet
4 Annexes

Définition, exemples et premières propriétés

Définition

La convolution de Dirichlet de deux fonctions arithmétiques f et g, est la fonction, généralement notée f * g définie par^[2] :

$\forall n \in \N^* \quad (f\star g) (n) = \sum_{ab = n} f(a)g(b),\quad a,b \in \N^*$

Exemples

Si f est la fonction 1_F, c'est à dire celle qui vaut 0 partout sauf en 1 où elle vaut 1, et si g est une fonction arithmétique quelconque, on dispose de l'égalité :

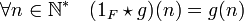
$\forall n \in \N^* \quad (1_F\star g) (n) = g(n)$

L'ensemble F des fonctions arithmétiques admet un élément neutre, la fonction 1_F.

Si φ désigne l'indicatrice d'Euler, Id la fonction identité, qui à n associe n et c₁ la fonction constante 1, on dispose de l'égalité^{[Note 2]} :

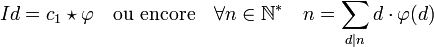
$Id = c_1\star \varphi \quad\text{ou encore}\quad \forall n \in \N^*\quad n = \sum_{d|n} d\cdot\varphi(d)$

Ici, les symboles d|n désignent l'ensemble des diviseurs entiers positifs de n.

Premières propriétés

Dans toute la suite de l'article F désigne l'ensemble des fonctions arithmétiques. La convolution de Dirichlet possède des propriétés communes à beaucoup de lois de composition internes :

La convolution de Dirichlet est commutative :

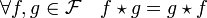
$\forall f,g \in \mathcal F \quad f\star g = g\star f$

Cette propriété est une conséquence directe de la définition.

La convolution de Dirichlet est associative :

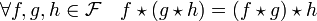
$\forall f,g,h \in \mathcal F \quad f\star (g\star h) = (f\star g)\star h$

La démonstration provient du caractère symétrique de la formulation suivante :

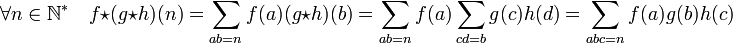
$\forall n \in \N^*\quad f\star (g\star h)(n) = \sum_{ab=n}f(a)(g\star h)(b) = \sum_{ab=n}f(a)\sum_{cd=b}g(c)h(d)=\sum_{abc=n}f(a)g(b)h(c)$

La convolution de Dirichlet est distributive par rapport à l'addition :

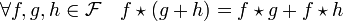
$\forall f,g,h \in \mathcal F \quad f\star (g + h) = f\star g + f\star h$

La démonstration est aussi élémentaire que la précédente :

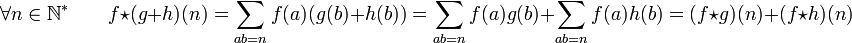
$\forall n \in \N^*\quad\quad f\star (g + h)(n) = \sum_{ab = n} f(a)(g(b)+h(b)) = \sum_{ab = n} f(a)g(b)+\sum_{ab = n} f(a)h(b)=(f\star g)(n) + (f\star h)(n)$

Le premier exemple montre que :

La convolution de Dirichlet admet un élément neutre, c'est la fonction partout nulle sauf en 1 où elle vaut 1.

Dans la suite de l'article, l'élément neutre est noté 1_F.

Il est possible de résumer ces différentes propriétés par :

L'ensemble F des fonctions arithmétiques munis de l'addition et de la convolution de Dirichlet forme un anneau commutatif unitaire.

Unitaire signifie ici que l'anneau contient un élément neutre pour la deuxième loi de composition interne.

Fonction multiplicative

Groupe des fonctions multiplicatives

Article détaillé : Fonction multiplicative.

L'anneau des fonctions arithmétiques n'est pas un corps. Il contient des éléments nilpotents, comme par exemple la fonction f nulle partout, sauf en 2 où elle vaut 1. cette fonction vérifie l'égalité f * f = 0.

Le groupe des unités de l'anneau des fonctions arithmétiques est composé des fonctions ayant une image de 1 non nulle^[3].

Le groupe des unités est constitué des éléments ayant un inverse pour le produit de Dirichlet. Les fonctions multiplicatives, par définition, ont pour image de 1 la valeur 1. Elles sont donc toutes inversibles. De plus :

L'ensemble M des fonctions multiplicatives, muni de la convolution de Dirichlet, forme un groupe abélien^[3].

En conséquence, le produit de deux fonctions multiplicatives est multiplicatif.

démonstrations

Toute fonction arithmétique f ayant pour image de 0 une valeur différente de 0 est inversible pour la convolution :

Soit g la fonction définie par récurrence de la manière suivante :

$g(1)=f(1)^{-1}\quad\text{et}\quad \forall n \ge 2 \quad g(n) = -f(1) \sum_{ab=n,\; b\neq n} f(a)g(b)$

Par construction, (f * g(1)) = 1. Cette égalité, ainsi que le calcul suivant démontre la proposition.

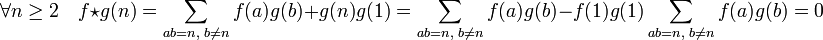
$\forall n \ge 2 \quad f\star g(n) = \sum_{ab=n,\;b\neq n} f(a)g(b) + g(n)g(1) = \sum_{ab=n,\;b\neq n}f(a)g(b) - f(1)g(1)\sum_{ab=n,\;b\neq n}f(a)g(b)=0$

L'ensemble des fonctions multiplicatives muni de la convolution est un groupe abélien :

L'associativité, la commutativité et l'existence d'un élément neutre sont déjà établis. Il suffit de démontrer que la convolution de deux fonctions multiplicatives f * g est multiplicative et que l'inverse pour la convolution d'une fonction multiplicative est aussi multiplicative.

Montrons tout d'abord que le produit f * g est multiplicatif. Si p est un nombre premier, s un entier strictement positif et n un entier strictement positif, premier avec p, il suffit de montrer que :

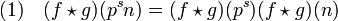
$(1)\quad (f\star g)(p^sn) = (f\star g)(p^s)(f\star g)(n)\;$

Une récurrence sur le nombre de facteurs premiers de m, un entier strictement positif, montre alors que (f * g)(m.n) = (f * g)(m)(f * g)(n). L'égalité (1) résulte du calcul suivant :

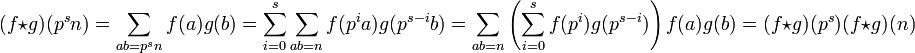
$(f\star g)(p^sn) = \sum_{ab=p^sn}f(a)g(b)= \sum_{i=0}^s\sum_{ab=n}f(p^ia)g(p^{s-i}b)=\sum_{ab=n}\left(\sum_{i=0}^sf(p^i)g(p^{s-i})\right)f(a)g(b)=(f\star g)(p^s)(f\star g)(n)$

Soit f * la fonction multiplicative égale à l'inverse de f sur les puissances des nombres premiers. La convolution de f * et de f est une fonction multiplicative, égale à 1_F sur les puissances des nombres premiers. La seule fonction multiplicative vérifiant cette propriété est 1_F, ce qui montre que f * est bien l'inverse de f pour la convolution.

Fonction de Möbius

Article détaillé : Fonction de Möbius.

La fonction de Mobius, généralement notée μ est définie par l'équation : Id = c₁ * μ. C'est donc l'inverse de la fonction constante 1. Un calcul^{[Note 3]} montre que si n est entier strictement positif sans facteur carré et si k est le nombre de nombres premiers qui divise n, μ(n) = (-1)^k. Si un carré parfait différent de 1 divise n, μ(n) = 0.

L'inverse de la fonction constante 1 joue un rôle particulier, vis à vis de la convolution. Soit f une fonction arithmétique et g une fonction définie par l'égalité g = c₁ * f. La fonction μ permet d'obtenir une expression de f à l'aide de g, plus exactement f = μ * g. Cette égalité est obtenue en appliquant une convolution par μ sur l'égalité définissant g. Ce résultat porte le nom de formule d'inversion de Möbius^[4].

Un exemple d'usage de la formule est son application sur l'indicatrice d'Euler. Cette fonction vérifie l'égalité Id = c₁ * φ. La formule d'inversion montre que :

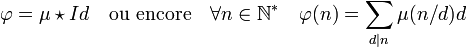
$\varphi = \mu \star Id\quad\text{ou encore}\quad \forall n \in \N^*\quad \varphi(n) = \sum_{d|n} \mu(n/d)d$

Fonction totalement multiplicative

Une fonctions f est dite totalement multiplicative si elle vaut 1 en 1 et si :

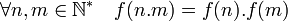
$\forall n,m \in \N^* \quad f(n.m) = f(n).f(m)$

Les fonctions totalement multiplicatives jouent un rôle en arithmétique. En théorie algébrique des nombres les caractères de Dirichlet sont des fonctions totalement multiplicatives. Leurs usages est à la base de la démonstration du théorème de la progression arithmétique de Dirichlet, à l'origine du développement du concept de la convolution de l'article^[5]. En théorie analytique des nombres, les fonctions f_s, qui à n associe n^s, où s est un nombre complexe, sont utilisées pour étudier la fonction zêta de Riemann ainsi que la fréquence de certains nombres particuliers, comme les nombres premiers.

Le calcul de l'inverse pour la convolution de ces fonctions est particulièrement aisé^[6] :

Soit f une fonction totalement multiplicative, son inverse est la fonction μ.f, qui à un entier strictement positif n associe μ(n).f(n).

La démonstration est la conséquence du calcul suivant :

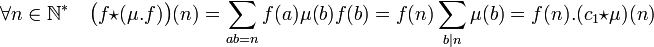
$\forall n \in \N^* \quad \big(f\star(\mu.f)\big)(n) = \sum_{ab=n}f(a)\mu(b)f(b)=f(n)\sum_{b|n}\mu(b)= f(n).(c_1\star\mu)(n)$

Par définition, la fonction c₁ * μ est égal à 1_F l'élément neutre, ou encore la fonction qui vaut 1 en 1 et 0 partout ailleurs. Il suffit alors de remarquer que f(1) est égal à 1 pour conclure.

Si la convolution de deux fonctions totalement multiplicatives est multiplicative, en revanche elle n'est pas nécessairement totalement multiplicative. Par exemple la convolution c₁ * c₁ correspond à la fonction qui à n associe son nombre de diviseurs. Cette fonction arithmétique n'est pas totalement multiplicative, l'image de 2 est égale à 2 et celle de 4 à 3.

Série L de Dirichlet

Si f est une fonction arithmétique, on définit sa série L (série de Dirichlet) par

$L(f,s) = \sum_{n=1}^\infty \frac{f(n)}{n^s}$

pour les arguments complexes s pour lesquels la série converge (s'il en existe). La multiplication des séries L est compatible avec la convolution de Dirichlet dans le sens suivant :

$L(f,s) L(g,s) = L(f*g,s)\,$

pour tous les s pour lesquels les deux séries du côté gauche convergent, l'une des deux en tout cas convergeant ABSOLUMENT (Noter que la simple convergence des deux séries à gauche N'IMPLIQUE PAS celle de la série à droite!). Ceci est ressemblant au théorème de convolution si on pense aux séries L comme une transformation de Fourier.

Annexes

Notes

↑ De manière plus générale, les suites arithmétiques sont à valeurs dans un corps commutatif quelconque
↑ Cette égalité est démontrée dans l'article Indicatrice d'Euler
↑ Voir l'article Fonction de Möbius

Références

↑ Dirichlet Beweis eines Satzes über die arithmetische Progression Bericht über die Verhandlungen der Königlich Preussischen Akademie der Wissenschaften, S. 108-110 p.307-312 1837
↑ F. Badiou, Formule d'inversion de Möbius Séminaire Delange-Pisot-Poitou Théorie des nombres tome 2 Exp. 1 p 01
↑ ^{a et b} F. Badiou, Formule d'inversion de Möbius Séminaire Delange-Pisot-Poitou Théorie des nombres tome 2 Exp. 1 p 02
↑ Cours et activités en arithmétiques pour les classes terminales par l'IREM de Marseille p 77
↑ G. H. Hardy E. M. Wright An Introduction to the Theory of Numbers, Oxford (5^ième édition) Clarendon Press, pp. 13-14 1979
↑ F. Badiou, Formule d'inversion de Möbius Séminaire Delange-Pisot-Poitou Théorie des nombres tome 2 Exp. 1 p 03

Bibliographie

Jean-Benoît Bost, Pierre Colmez et Philippe Biane La fonction Zêta, Éditions de l'École polytechnique Paris 2002 (ISBN 2730210113)
Harold Davenport's Multiplicative number theory, 3^ème edt Springer 2000 (ISBN 0387950974)

Portail des mathématiques

Ce document provient de « Convolution de Dirichlet ».

Catégories : Caractère de Dirichlet | Analyse harmonique discrète

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Produit de convolution de Dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Convolution De Dirichlet — Johann Peter Gustav Lejeune Dirichlet développe son produit en 1937 pour démontrer le théorème de la progression arithmétique. En mathématiques, la convolution de Dirichlet, encore appelée produit de convolution de Dirichlet ou produit de… … Wikipédia en Français
Convolution de dirichlet — Johann Peter Gustav Lejeune Dirichlet développe son produit en 1937 pour démontrer le théorème de la progression arithmétique. En mathématiques, la convolution de Dirichlet, encore appelée produit de convolution de Dirichlet ou produit de… … Wikipédia en Français
Convolution de Dirichlet — En mathématiques, la convolution de Dirichlet, encore appelée produit de convolution de Dirichlet ou produit de Dirichlet est une loi de composition interne définie sur l ensemble des fonctions arithmétiques, c est à dire des fonctions définies… … Wikipédia en Français
Dirichlet (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des nombres. Arithmétique… … Wikipédia en Français
Dirichlet (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des nombres. Arithmétique… … Wikipédia en Français
Fonction de Dirichlet — Dirichlet (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des… … Wikipédia en Français
Convolution — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Convolution », sur le Wiktionnaire (dictionnaire universel) Le terme convolution désigne deux types d… … Wikipédia en Français
Noyau de Dirichlet — Pour les articles homonymes, voir noyau. En mathématiques, le n ième noyau de Dirichlet – nommé ainsi en l honneur du mathématicien allemand Johann Dirichlet – est le polynôme trigonométrique défini par : . C est donc une fonction 2π… … Wikipédia en Français
Noyau de dirichlet — Pour les articles homonymes, voir noyau. En mathématiques, et plus particulièrement dans la théorie des séries de Fourier, le noyau de Dirichlet est un polynôme trigonométrique qui permet notamment d améliorer la convergence des séries de Fourier … Wikipédia en Français
Conditions De Dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Produit de convolution de Dirichlet

Convolution de Dirichlet

Sommaire