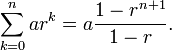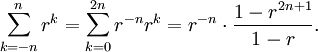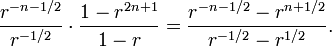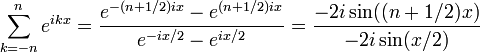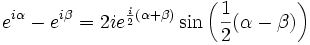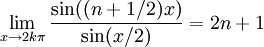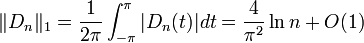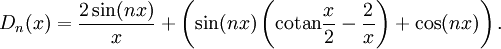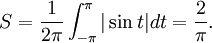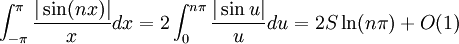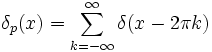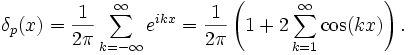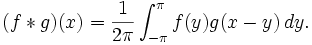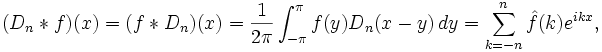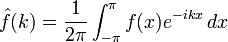Noyau de dirichlet

Noyau de Dirichlet

Pour les articles homonymes, voir noyau.

En mathématiques, et plus particulièrement dans la théorie des séries de Fourier, le noyau de Dirichlet est un polynôme trigonométrique qui permet notamment d'améliorer la convergence des séries de Fourier. Il a pour expression :

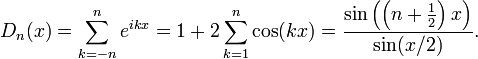
$D_n(x)=\sum_{k=-n}^n e^{ikx}=1+2\sum_{k=1}^n\cos(kx)=\frac{\sin\left(\left(n+\frac{1}{2}\right)x\right)}{\sin(x/2)}.$

Pour cette dernière expression, la fraction n'est pas définie aux points multiples entiers de $2π$ , mais se prolonge par continuité en une fonction de classe 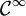$\mathcal{C}^\infty$ par les valeurs :

D n (2 k π) = 2 n + 1.

Le noyau de Dirichlet intervient aussi en optique, pour rendre compte des franges et des compositions d'ondes cohérentes.

Cette expression est nommée ainsi en l'honneur de Johann Dirichlet, un mathématicien allemand.

Sommaire

1 Considérations élémentaires
- 1.1 Équivalence des deux écritures du noyau de Dirichlet
  - 1.1.1 Variante
  - 1.1.2 Le cas e^ix = 1
- 1.2 Propriétés du noyau de Dirichlet
2 Opérateur associé
3 Introduction au formalisme des distributions

Considérations élémentaires

Équivalence des deux écritures du noyau de Dirichlet

L'identité trigonométrique qui apparaît au début de l'article peut être établie par le calcul d'une somme d'une série géométrique de raison $e i x$ .

Rappelons que la somme partielle au rang n d'une série géométrique de raison r≠1 vaut

$\sum_{k=0}^n a r^k=a\frac{1-r^{n+1}}{1-r}.$

Ici c'est une somme symétrique qui nous intéresse

$\sum_{k=-n}^n r^k=\sum_{k=0}^{2n} r^{-n}r^k=r^{-n}\cdot\frac{1-r^{2n+1}}{1-r}.$

L'expression à gauche du symbole égal nous incite à penser que la somme est une fonction symétrique de r et 1/r. Mais dans l'expression à droite du symbole égal, il est difficile de diagnostiquer une telle symétrie par rapport à ces deux quantités. Le remède est de multiplier à la fois le numérateur et le dénominateur par r^-1/2, pour obtenir

$\frac{r^{-n-1/2}}{r^{-1/2}}\cdot\frac{1-r^{2n+1}}{1-r}=\frac{r^{-n-1/2}-r^{n+1/2}}{r^{-1/2}-r^{1/2}}.$

Dans le cas où r = e^ix nous avons:

$\sum_{k=-n}^n e^{ikx}=\frac{e^{-(n+1/2)ix}-e^{(n+1/2)ix}}{e^{-ix/2}-e^{ix/2}}=\frac{-2i\sin((n+1/2)x)}{-2i\sin(x/2)}$

et alors « -2i » disparaît.

Variante

Un autre guide pour le calcul peut être l'idée suivante : le calcul de la somme ou de la différence de deux complexes de même module se fait en introduisant l'angle moitié

$e^{i\alpha}-e^{i\beta}=2ie^{\frac i2(\alpha+\beta)}\sin \left(\frac12(\alpha-\beta)\right)$

On procède ainsi au numérateur et au dénominateur.

Le cas $e i x = 1$

L'égalité des deux expressions a été établie pour 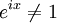$e^{ix}\neq 1$ , c'est-à-dire pour des valeurs de x non multiples de $2π$ .

L'expression 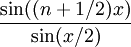$\frac{\sin((n+1/2)x)}{\sin(x/2)}$ peut donc être prolongée par continuité en tout point multiple de $2π$

$\lim\limits_{x\to 2k\pi} \frac{\sin((n+1/2)x)}{\sin(x/2)} = 2n+1$

Propriétés du noyau de Dirichlet

C'est un polynôme trigonométrique, donc une fonction 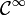$\mathcal C^\infty$ , 2π périodique.
Il est pair
Sa valeur moyenne est 1 ;
comportement asymptotique de la norme de la convergence en moyenne

$\|D_n\|_1=\frac1{2\pi}\int_{-\pi}^{\pi} |D_n(t)| d t =\frac4{\pi^2}\ln n+O(1)$

Démonstration

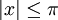L'idée générale est de se ramener à une fonction sinus cardinal. En effet, pour $|x|\leq \pi$ ,

$D_n(x)=\frac{2\sin (nx)}{x} + \left(\sin (nx) \left(\operatorname{cotan} \frac x 2-\frac2x\right)+\cos (nx)\right).$

On reconnaît dans le second terme de cette somme une fonction prolongeable par continuité en 0, donc continue, et bornée indépendamment de n. Dès lors, il suffit de montrer la propriété pour le premier terme de la somme qui est un sinus cardinal.

Pour ce dernier, il s'agit d'un résultat classique : on introduit la valeur moyenne du numérateur

$S=\frac1{2\pi}\int_{-\pi}^\pi |\sin t| d t = \frac2\pi.$

Alors

$\int_{-\pi}^\pi \frac{|\sin (nx)|}{x}dx =2\int_0^{n\pi} \frac{|\sin u|}{u}du = 2 S \ln (n\pi) +O(1)$

La démonstration, se faisant par intégration par parties ou comparaison série-intégrale, est détaillée dans l'article sinus cardinal.

Opérateur associé

Le n-ième terme de la série de Fourier d'une fonction f 2π périodique intégrable s'écrit :

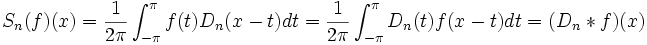$S_n(f)(x)=\frac1{2\pi}\int_{-\pi}^{\pi} f(t) D_n(x-t) dt = \frac1{2\pi}\int_{-\pi}^{\pi} D_n(t) f(x-t) dt=(D_n*f)(x)\,$ ;

L'identité précédente est un produit de convolution, ou l'application d'un opérateur à noyau.

C'est à partir de cette expression et des propriétés du noyau de Dirichlet qu'on démontre le théorème de Dirichlet sur la convergence des séries de Fourier.

Cet opérateur est un opérateur borné sur l'espace des fonctions continues, dont la norme d'opérateur est majorée par $\|D_n\|_1$ .

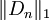En spécialisant l'étude en un point x particulier, l'application 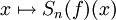$x\mapsto S_n(f)(x)$ a pour norme d'opérateur 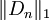$\|D_n\|_1$ lui même, qui tend vers l'infini avec n. À l'aide du théorème de Banach-Steinhaus, on peut en déduire qu'il existe des fonctions continues dont la série de Fourier diverge au point x.

Introduction au formalisme des distributions

Le noyau de Dirichlet est 2π fois la somme d'ordre n du développement en séries de Fourier d'une « fonction », en distribution, de période 2π donnée par

$\delta_p(x)=\sum_{k=-\infty}^\infty\delta(x-2\pi k)$

où δ est la fonction delta de Dirac, qui n'est pas vraiment une fonction, dans le sens d'application d'un ensemble vers un autre, mais est plutôt une «fonction généralisée», aussi appelée une distribution. En d'autres termes, le développement en série de Fourier de cette « fonction » s'écrit

$\delta_p(x)=\frac{1}{2\pi}\sum_{k=-\infty}^\infty e^{ikx}=\frac{1}{2\pi}\left(1+2\sum_{k=1}^\infty\cos(kx)\right).$

Cette « fonction périodique delta » est l'élément neutre pour le produit de convolution défini sur l'ensemble des fonctions de période 2π par

$(f*g)(x)=\frac{1}{2\pi}\int_{-\pi}^\pi f(y)g(x-y)\,dy.$

Autrement dit,

pour toute fonction f de période 2π,

f * δ p = δ p * f = f

Le produit de convolution de D_n avec n'importe quelle fonction f de période 2π est égal à la somme d'ordre n du développement en série de Fourier de f, i.e., nous avons

$(D_n*f)(x)=(f*D_n)(x)=\frac{1}{2\pi}\int_{-\pi}^\pi f(y)D_n(x-y)\,dy=\sum_{k=-n}^n \hat{f}(k)e^{ikx},$

où

$\hat{f}(k)=\frac{1}{2\pi}\int_{-\pi}^\pi f(x)e^{-ikx}\,dx$

est le kème coefficient de Fourier de f.

Portail des mathématiques

Ce document provient de « Noyau de Dirichlet ».

Catégories : Série de Fourier | Fonction remarquable | Trigonométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Noyau de dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Noyau de Dirichlet — Pour les articles homonymes, voir noyau. En mathématiques, le n ième noyau de Dirichlet – nommé ainsi en l honneur du mathématicien allemand Johann Dirichlet – est le polynôme trigonométrique défini par : . C est donc une fonction 2π… … Wikipédia en Français
Noyau de Fejer — Noyau de Fejér En mathématiques, en analyse fonctionnelle et harmonique, le noyau de Fejér est une fonction permettant de calculer les sommes partielles de Fejér. Expression mathématique On peut établir l expression du noyau de Fejér à partir du… … Wikipédia en Français
Noyau de fejér — En mathématiques, en analyse fonctionnelle et harmonique, le noyau de Fejér est une fonction permettant de calculer les sommes partielles de Fejér. Expression mathématique On peut établir l expression du noyau de Fejér à partir du noyau de… … Wikipédia en Français
Dirichlet (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des nombres. Arithmétique… … Wikipédia en Français
Noyau dur — Noyau Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Dirichlet — Johann Peter Gustav Lejeune Dirichlet Pour les articles homonymes, voir Dirichlet (homonymie). Johann Peter Gustav Lejeune Dirichlet Johann Peter Gustav Lejeune Dirichlet ( … Wikipédia en Français
Noyau de Fejér — En mathématiques, en analyse fonctionnelle et harmonique, le noyau de Fejér est une fonction permettant de calculer les sommes partielles de Fejér. Expression mathématique On peut établir l expression du noyau de Fejér à partir du noyau de… … Wikipédia en Français
Dirichlet (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des nombres. Arithmétique… … Wikipédia en Français
Noyau — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Noyau », sur le Wiktionnaire (dictionnaire universel) De manière générale, un noyau est la partie… … Wikipédia en Français
Noyau de Poisson — En théorie du potentiel, le noyau de Poisson est un opérateur intégral utilisé pour résoudre le problème de Dirichlet en dimension 2. Plus précisément, il donne des solutions à l équation de Laplace en deux dimensions vérifiant les conditions aux … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Noyau de dirichlet